KMP

把以前写的 KMP 放上来。

错别字有点多（

---

KMP

盲猜今天会有很多人听不懂郭老师讲的KMP，于是提前发一篇有关 KMP 的博客。

建议搭配KMP模板题解食用。

引入

对于字符串匹配问题，我们定义需要查找字符串叫“模式串”（长度为 \(M\)），被查找字符串叫“文本串”（长度为 \(N\)）。

暴力查找或使用 C++ STL string.find 的最坏时间复杂度都为 \(\mathcal{O}(N \times M)\)，而在某些题目里无法通过，需要更优的算法来解决。

KMP分析

在暴力查找时因为会查找到许多无用的信息而导致效率过低，而我们可以从这一点下手，尝试过滤掉无用的查找来提升效率。

假设当前匹配到了文本串的第 \(i\) 位，模式串的第 \(j\) 位，也就是说文本串的第 \(i - j + 1\) 到 \(i\) 位的字串与模式串长度为 \(j\) 的前缀相同。

用一张图来理解：

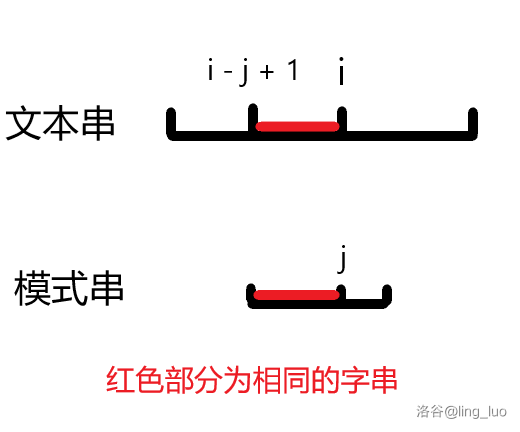
如果文本串的 \(i + 1\) 位与模式串第 \(j + 1\) 位不同，暴力查找就会将 \(j\) 置为 \(0\)，将 \(i\) 设为 \(i - j + 2\) 重新开始匹配。

在上面的过程中，\(j\) 经常会多次重置为 \(0\) 导致循环次数增加。

如果可以不重置 \(i\) 并且将 \(j\) 每次置为某个最大值使得对应的字串相同，那么我们可以几乎把枚举 \(j\) 的那一重循环优化掉。（可以感性理解为我们可以不用枚举 \(j\) 而是直接将 \(j\) 跳到它应该在的地方）

对于上面要求的字串，其实就是字符串的最长真公共前后缀。

还是用图来理解：

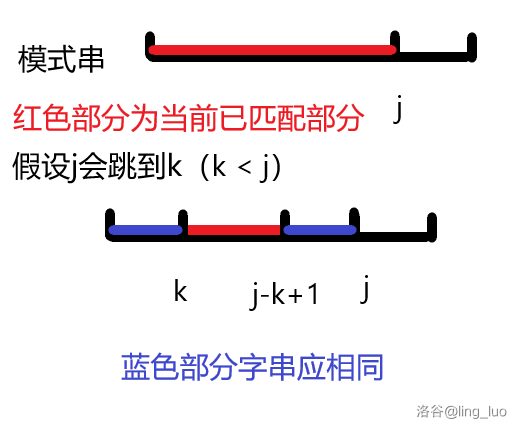
因为当前文本串的第 \(i - j + 1\) 到 \(i\) 位的字串与模式串长度为 \(j\) 的前缀相同，所以其实可以只用考虑模式串就好了。

那么将 \(j\) 跳到 \(k\) 后的情况应该是这样的：

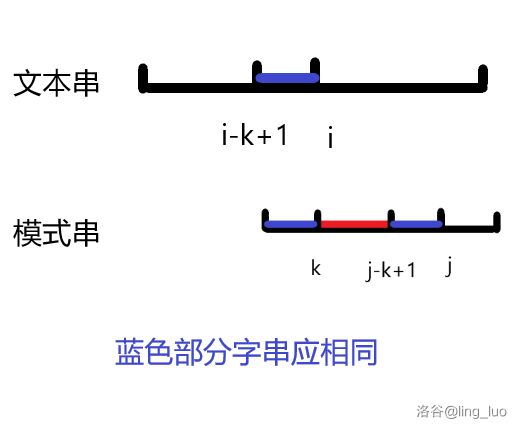
对比上面几张图，可以将这个过程理解为不停地移动模式串来匹配。

到这里应该就能大概理解了。

而现在的问题就是如何快速地求出模式串每个不同的 \(j\) 对应的 \(k\) 的值。

（PS：其实这个 \(k\) 就是KMP的失配数组，下文用 \(nxt_{j}\) 来表示 \(j\) 对应的应该跳到的位置。）

在上面找模式串已匹配前缀的最长真公共前后缀时，我们并没有用到文本串，于是可以考虑将模式串与它自己匹配一次来求出 \(nxt\) 数组。

首先，\(nxt_{0} = nxt_{1} = 0\)，因为这两种情况都只能跳到 \(0\)。

假设当前处理到模式串的第 \(i\) 位，且模式串的最长匹配前缀长度为 \(j\)（可以将前一个模式串理解为文本串），\(nxt_{0} \sim nxt_{i - 1}\) 都处理完毕，如何得到 \(nxt_{i}\)？

• 如果模式串的第 \(j + 1\) 位与第 \(i\) 位相同，那么将 \(j\) 加一并且将 \(nxt_{i}\) 设为 \(j\)。

• 如果 \(j\) 不为 \(0\) 且模式串的第 \(j + 1\) 位与第 \(i\) 位不同，那么将 \(j\) 设为 \(nxt_{j}\) 直到 \(j\) 为 \(0\) 或模式串的第 \(j + 1\) 位与第 \(i\) 位相同。

对于第一种情况应该比较好理解，就是说最长匹配前缀的下一位与当前待匹配的位置相同，那么就可以直接进行匹配。

对于第二种情况，因为下一位不能匹配所以无法算出 \(nxt_{i}\) 的值（因为它当前匹配的是 \(i - 1\)），而 \(nxt_{j}\) 是已知的并且根据 \(nxt\) 的定义，我们将 \(j\) 设为 \(nxt_{j}\) 是符合要求并且最优的，所以将 \(j\) 设为 \(nxt_{j}\) （注意，这里将 \(j\) 设为 \(nxt_{j}\) 后可能下一位仍不匹配，所以此操作需循环进行）。

这样，\(nxt\) 数组就处理完了。（如果不理解可以对照代码再看一下或者去看一下别的题解的不同的描述。）

而对于文本串和模式串的匹配也是类似的，不同点就是将求 \(nxt_{i}\) 的部分改为判断 \(j\) 是否为 \(M\)（意思就是模式串是否匹配完毕）。

注意，如果某个时刻模式串匹配完毕后那么应将 \(j\) 设为 \(nxt_{j}\)，因为此时 \(j\) 不存在下一位。

代码实现

（\(a\) 为文本串，\(b\) 为模式串）

\(nxt\) 数组：

int j = 0;
for(int i = 2; i <= m; ++i) {
	while(j && b[j + 1] != b[i]) j = nxt[j];//第二种情况 
	if(b[j + 1] == b[i]) ++j;//第一种情况
	nxt[i] = j;//处理nxt 
}

匹配：

vector<int> ans;
int j = 0;
for(int i = 1; i <= n; ++i) {
	while(j && b[j + 1] != a[i]) j = nxt[j];//第二种情况 
	if(b[j + 1] == a[i]) ++j;//第一种情况
	if(j == m) {//判断是否匹配完毕 
		ans.push_back(i - j + 1);
		j = nxt[j];//因为j下一位为空，所以需将j设为nxt_j 
	}
}

以上就是KMP的全部内容啦。

总结

KMP 是一种思维量巨大，代码简单，效率高的算法，难点在于如何理解失配数组。

KMP 里面有许多嵌套的非常复杂的地方而且处理失配数组的地方真的很难描述，如果发现有问题欢迎指出。

有问题可以问我qwq