P9266 [PA 2022] Nawiasowe podziały 题解

模拟赛 T1 放了这道题的加强版，打了一上午的三 $\log$ 做法结果发现 $n$ 被毒瘤搬题人开到了 $5 \times 10^{5}$，直接气吐血。

---

这种题看着就很有 dp 的感觉，但是状态太多开不下。发现是“强制划分为 $k$ 段”这个条件很烦人，于是用 wqs 二分把这一维优化掉。

具体地，二分一个 $\Delta$，表示每分一段就会多出来的代价，在 dp 的过程中忽略强制选 $k$ 段的限制，直接统计最小代价并记录划分的段数。如果段数比 $k$ 小则将 $\Delta$ 调小，否则调大。

考虑 check 怎么写，先把 dp 的状态转移方程写出来：

$$ dp_{i} = \min\limits_{0 \leqslant j < i}\left\{dp_{j} + w(j + 1, i) + \Delta\right\} $$

其中 $w(l, r)$ 表示字符串的子串 $S[l..r]$ 中有多少个合法括号子串。

从直觉上来看，上面这个式子是满足决策单调性的，因为在 $r$ 逐渐增大的过程中，最优决策的 $l$ 肯定也是逐渐增大或不变才能保证代价最小，如果某个时刻 $l$ 倒退了的话那么在前面的决策中 $l$ 也应该倒退才对。

或者说可以证明一下 $w(l, r + 1) + w(l - 1, r) \leqslant w(l - 1, r + 1) + w(l, r)$。这个东西我只会一种比较感性的证明方式：发现 $S[l..r]$ 这里的子串贡献是一定的，所以只用考虑 $l - 1$ 和 $r + 1$ 处的贡献。

而每个在 $[l, r]$ 中可以和 $l - 1$ 产生贡献的位置会在 $w(l - 1, r)$ 和 $w(l - 1, r + 1)$ 中产生贡献，并且它们的贡献相同。$r + 1$ 同理。

但是在 $w(l - 1, r + 1)$ 中 $l - 1$ 和 $r + 1$ 还可能产生贡献，所以 $w(l - 1, r) + w(l, r + 1) \leqslant w(l - 1, r + 1) + w(l, r)$。

有了这个我们就可以利用决策单调性优化 dp 了，但是因为决策的过程中有 dp 本身，所以要使用 CDQ 分治来规避掉未知的 dp 值无法转移的情况。

现在你已经打出了 wqs 二分，短短几行的 CDQ 分治以及决策单调性优化 dp 的函数，但是你发现 $w(l, r)$ 无法快速计算，这让人很头疼。

如果你做过 CF868F 那么你应该能想到可以利用一个类莫队的方法来计算 $w(l, r)$ 的值，并且它的时间复杂度是均摊单次 $\mathcal{O}(1)$ 的。

但这也是本题的三 $\log$ 做法最难的部分。（也许不是，我在赛后听到学长在谈论什么染色的方法，但是我不会。）

假设我们已经维护好一段子串的贡献了，现在要在这个子串右端加入一个右括号 )。

下面为了方便并且直观，使用了许多不同的颜色来代表不同的括号。

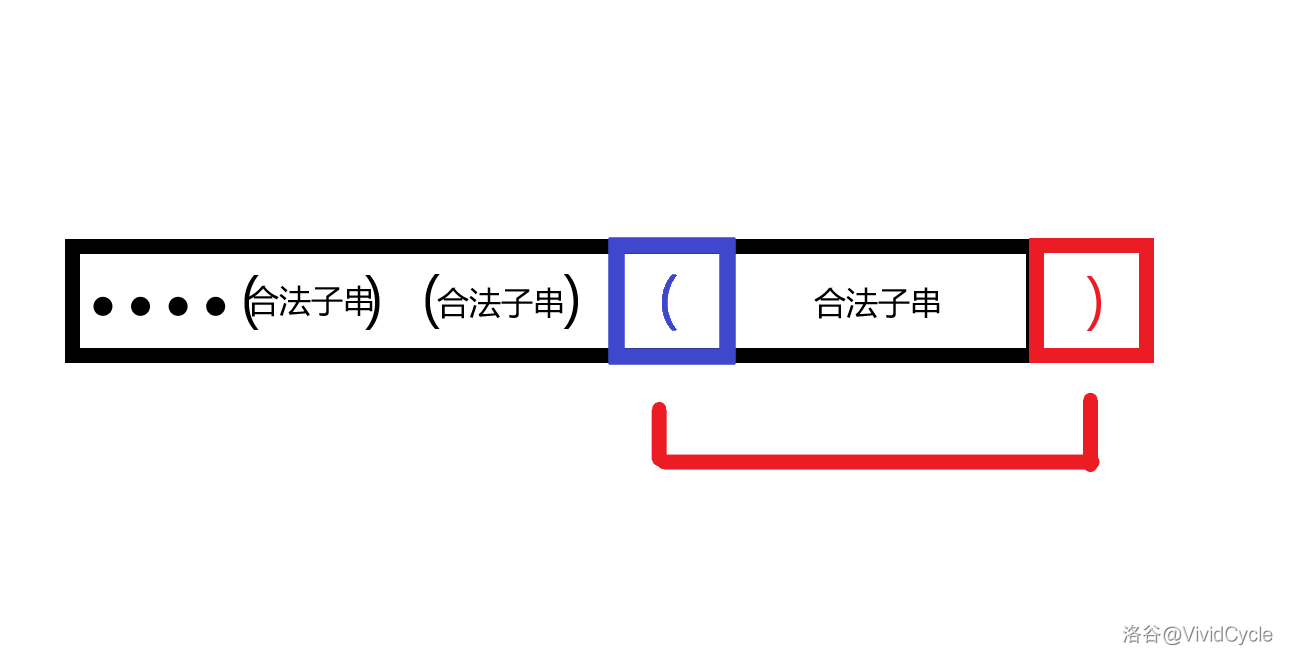
上面的红色右括号 $\color{red}\texttt{)}$ 表示新加入的右括号，蓝色左括号 $\color{blue}\texttt{(}$ 表示在原串中与 $\color{red}\texttt{)}$ 相匹配的括号。

（注意，因为这个字符串是不变的，所以每个括号的匹配情况也是不变的，只是有些时候匹配的括号不在当前区间内而已。并且两个匹配的括号之间的子串一定是合法子串，否则它们无法匹配）

如果 $\color{blue}\texttt{(}$ 不在当前区间 $[l, r]$ 内那肯定无法造成贡献，所以只考虑 $\color{blue}\texttt{(}$ 在区间 $[l, r]$ 内的情况。

首先 $\color{blue}\texttt{(}$ 和 $\color{red}\texttt{)}$ 一定可以产生 $1$ 的贡献。并且在 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 前“拼接”一个合法子串又能产生大小为 $1$ 的贡献，“拼接”之后还可以再“拼接”继续产生贡献。可以一直重复下去。

所以只要知道 $\color{blue}\texttt{(}$ 前有多少个独立且相邻的合法子串，独立是指这些子串没有包含关系，相邻是指将这些合法子串按顺序排列后，它们之间没有多余括号，在上图已经画出来的部分就有两个独立且相邻的合法子串。

直接扫一遍显然是不优的，可以构造 ()()()()() 这样的数据卡掉，于是考虑将贡献“提前计算”，储存到 $\color{red}\texttt{)}$ 的位置，当加入 $\color{red}\texttt{)}$ 时把这个贡献加上。把这个“提前计算”的贡献称为 $sum$。

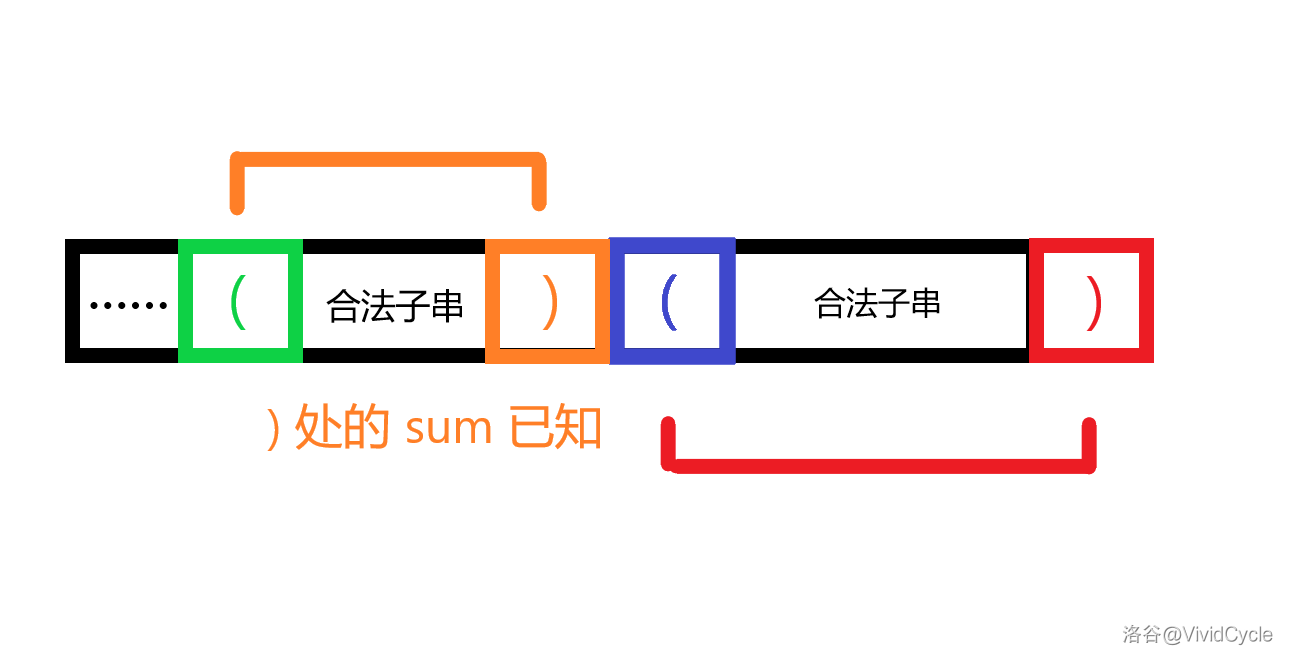
这里的 $\color{lime}\texttt{(}\color{black}\cdots\color{orange}\texttt{)}$ 是与 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 直接相邻的一个合法子串，考虑利用 $\color{orange}\texttt{)}$ 的 $sum$ 推出 $\color{red}\texttt{)}$。

注意到 $\color{lime}\texttt{(}\color{black}\cdots\color{orange}\texttt{)}$ 和 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 也是独立且相邻的，而在上述定义中所有和 $\color{lime}\texttt{(}\color{black}\cdots\color{orange}\texttt{)}$ 独立且相邻的合法子串再加上 $\color{lime}\texttt{(}\color{black}\cdots\color{orange}\texttt{)}$ 本身，它们也是和 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 独立且相邻的，所以 $\color{red}\texttt{)}$ 处的 $sum$ 值为 $\color{orange}\texttt{)}$ 处的 $sum + 1$。

左括号的情况类似，如果无法理解你就把上面的图旋转 180 度看就行（

但是，我们还漏掉了一种情况：我们在 $\color{lime}\texttt{(}\color{black}\cdots\color{orange}\texttt{)}$ 右端“拼接”上了 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 后 $\color{lime}\texttt{(}$ 处的 $sum$ 值并没有更新（它理应是 $2$ 但此时仍然是 $1$）。

暴力更新是显然不可以的，()()()()() 这样的数据同样能卡掉，每加入一个 () 都会将前面所有括号的 $sum$ 重新计算一遍。

这时我们要利用类莫队计算方法的特性：它只会在两边加入和删除。换句话说，我们只需要维护一个极长独立且相邻的合法子串段的左右端点处的 $sum$ 即可。

于是额外维护一个位置 $ps$，表示当前括号所处的极长独立且相邻的合法子串段的左/右端点。

（这里只需要维护一个 $ps$ 即可，因为维护右端点对 $\texttt{)}$ 的加入和删除操作没有意义，左端点对 $\texttt{(}$ 的加入和删除没有意义，而且这么做还可以大幅度减小码量。）

那么当我们在 $\color{lime}\texttt{(}\color{black}\cdots\color{orange}\texttt{)}$ 右端“拼接”$\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 后，只需要将 $\color{orange}\texttt{)}$ 处的 $ps$ 指向的位置的 $sum$ 值更改即可。注意这里还要同时维护 $\color{blue}\texttt{(}$，$\color{red}\texttt{)}$ 和 $\color{orange}\texttt{)}$ 的 $ps$ 指向的位置，这三个地方的 $ps$ 值。显然 $\color{blue}\texttt{(}$ 应指向 $\color{red}\texttt{)}$，$\color{red}\texttt{)}$ 和 $\color{orange}\texttt{)}$ 处的 $ps$ 指向的位置互相指向。

注意如果在 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 前面没有独立且相邻的合法子串，那么直接将 $\color{blue}\texttt{(}$ 和 $\color{red}\texttt{)}$ 的 $sum$ 设为 $1$ 即可，意义显然。

有了加入操作的经验，不难想到把“删掉一个括号造成的贡献”也提前计算储存起来。

事实上，可以直接用 $sum$ 表示这个贡献，因为一个括号不可能同时处于会被删除的状态和会被加入的状态。或者说，将 $sum$ 定义为一个括号改变自身状态后会造成的贡献。

把上面那张图搬下来一下。

假设待删除的括号是 $\color{red}\texttt{)}$，其余括号的意义不变。

删除括号后的贡献也用同样的方法考虑，一次删除减少的合法子串数为“和 $\color{blue}\texttt{(}\color{black}\cdots\color{red}\texttt{)}$ 独立且相邻的子串数”，同样地，我们需要减去 $\color{red}\texttt{)}$ 处的 $sum$ 大小的贡献。

继续考虑将 $\color{red}\texttt{)}$ 删除后会引起哪些位置的 $sum$ 的改变，它们应该是 $\color{blue}\texttt{(}$，$\color{red}\texttt{)}$，$\color{lime}\texttt{(}$，$\color{orange}\texttt{)}$ 和 $\color{red}\texttt{)}$ 处的 $ps$ 指向的位置，它们应分别改变为 $0$，$0$，$1$，$\color{red}\texttt{)}$ 处的 $sum - 1$ 和 $\color{red}\texttt{)}$ 处的 $ps$ 指向的位置的 $sum - 1$，这里的意义不用过多阐述。

你可能会有疑问：像 $\color{red}\texttt{)}$ 这样的位置都被删除掉了，为什么还要维护？因为 $\color{red}\texttt{)}$ 被删除后，它的状态就由“可以被删除”变为“可以被加入”，此时它的 $sum$ 就表示了它被加入后会产生的贡献，所以需要及时维护。

左括号仍然同理，你只需要将上面的图旋转 180 度看就可以了（

你可能会想到，我还没有说明在右侧加入左括号的情况和在左侧加入右括号的情况。这两种情况显然不会造成任何贡献，直接忽略即可。

因为左括号和右括号的情况是对称的（从“旋转 180 度”也可以看出来），所以只要打出来左括号的情况那么右括号也迎刃而解了。

贴一份代码，其中 check() 函数是 wqs 二分时的检查函数；CDQ(l, r) 函数是 CDQ 分治（作用在上文中已说明，需注意我这里脑抽打了个左闭右开的区间）；solve(dl, dr, l, r) 是决策单调性优化 dp 的函数，dl 和 dr 是待决策的区间，l 和 r 是可以转移的区间；calc 是类莫队计算 $w(l, r)$ 的函数；add 和 del 就是加入和删除括号时计算贡献的函数。

时间复杂度 $\mathcal{O}(n \log^{2} n \log V)$ 跑了两分半喜提最劣解！其中 $V$ 表示 wqs 二分时的值域。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n, k, l, r, delta, ans, L, R, res, p[100005], dp[100005], s[100005], sum[100005], ps[100005];
string str;
stack<int> stk;
void add(int pos) {
    if(str[pos] == '(') {
        if(p[pos] <= R) {
            if(str[p[pos] + 1] == '(' && p[p[pos] + 1] <= R) {
                sum[pos] = sum[p[pos] + 1] + 1;
                ps[pos] = ps[p[pos] + 1];
                ps[ps[pos]] = pos;
                ++sum[ps[pos]];
            }
            else sum[pos] = 1, ps[pos] = p[pos];
            ++sum[p[pos]];
            ps[p[pos]] = pos;
            res += sum[pos];
        }
    }
    if(str[pos] == ')') {
        if(p[pos] >= L) {
            if(str[p[pos] - 1] == ')' && p[p[pos] - 1] >= L) {
                sum[pos] = sum[p[pos] - 1] + 1;
                ps[pos] = ps[p[pos] - 1];
                ++sum[ps[pos]];
                ps[ps[pos]] = pos;
            }
            else sum[pos] = 1, ps[pos] = p[pos];
            ++sum[p[pos]];
            ps[p[pos]] = pos;
            res += sum[pos];
        }
    }
}
void del(int pos) {
    if(str[pos] == '(') {
        if(p[pos] <= R) {
            res -= sum[pos];
            if(str[p[pos] + 1] == '(' && p[p[pos] + 1] <= R) {
                --sum[ps[pos]];
                sum[p[pos] + 1] = sum[pos] - 1;
                sum[p[p[pos] + 1]] = 1;
                ps[p[p[pos] + 1]] = p[pos] + 1;
                ps[ps[pos]] = p[pos] + 1;
                ps[p[pos] + 1] = ps[pos];
                ps[pos] = 0;
            }
            else sum[pos] = 0, ps[pos] = 0;
            --sum[p[pos]];
            ps[p[pos]] = 0;
        }
        sum[pos] = 0;
    }
    if(str[pos] == ')') {
        if(p[pos] >= L) {
            res -= sum[pos];
            if(str[p[pos] - 1] == ')' && p[p[pos] - 1] >= L) {
                --sum[ps[pos]];
                sum[p[pos] - 1] = sum[pos] - 1;
                sum[p[p[pos] - 1]] = 1;
                ps[p[p[pos] - 1]] = p[pos] - 1;
                ps[ps[pos]] = p[pos] - 1;
                ps[p[pos] - 1] = ps[pos];
                ps[pos] = 0;
            }
            else sum[pos] = 0, ps[pos] = 0;
            --sum[p[pos]];
            ps[p[pos]] = 0;
        }
        sum[pos] = 0;
    }
}
ll calc(int l, int r) {
    while(L > l) add(--L);
    while(R < r) add(++R);
    while(L < l) del(L++);
    while(R > r) del(R--);
    return res;
}
void solve(int dl, int dr, int l, int r) {
    if(dl > dr || l > r) return;
    int mid = (dl + dr) >> 1, pos = l;
    ll mn = dp[l] + calc(l + 1, mid) + delta, tmp;
    for(int i = l; i <= r; ++i) {
        tmp = dp[i] + calc(i + 1, mid) + delta;
        if(tmp <= mn || (tmp == mn && s[i] > s[pos])) {
            pos = i, mn = tmp;
        }
    }
    if(mn < dp[mid] || (dp[mid] == mn && s[pos] + 1 > s[mid])) {
        dp[mid] = mn;
        s[mid] = s[pos] + 1;
    }
    solve(dl, mid - 1, l, pos);
    solve(mid + 1, dr, pos, r);
}
void CDQ(int l, int r) {
    if(l + 1 >= r) return;
    int mid = (l + r) >> 1;
    CDQ(l, mid);
    solve(mid, r - 1, l, mid - 1);
    CDQ(mid, r);
}
bool check() {
    fill(dp + 1, dp + 1 + n, 0x7f7f7f7f7f7f7f7f);
    dp[0] = 0;
    CDQ(0, n + 1);
    return s[n] >= k;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    cin >> n >> k >> str;
    str = '$' + str;
    for(int i = 1; i <= n; ++i) {
        if(str[i] == '(') p[i] = n + 1;
        else p[i] = 0;
    }
    for(int i = 1; i <= n; ++i) {
        if(str[i] == '(') stk.push(i);
        else if(!stk.empty()) {
            p[i] = stk.top();
            p[stk.top()] = i;
            stk.pop();
        }
    }
    L = 1, R = 0, res = 0;
    l = -10000000000ll, r = 10000000000ll;
    while(l <= r) delta = (l + r) >> 1, check() ? (ans = dp[n] - delta * k, l = delta + 1) : (r = delta - 1);
    cout << ans;
    cerr << '\n' << clock() << '\n';
    return 0;
}

---

话说我这份题解是不是对患有色盲症的同学有点不太友好qwq