关于不定积分
不定积分
原函数：
若 \(F,f\) 在区间 \(I\) 上均有定义，且 \(F'=f\) 。
则称 \(F\) 为 \(f\) 在区间 \(I\) 上的一个原函数。
常用公式：
\[\int x^{\alpha} dx =\dfrac{x^{\alpha+1}}{\alpha+1}+C \ \ ，
\int \dfrac{1}{x} dx =\ln|x|+C\\
\
\\
\
\int e^x dx =e^x+C\ \ ，\int a^x dx =\dfrac{a^x}{\ln a}+C\\
\
\\
\
\int \dfrac{1}{1+x^2} dx =\arctan x+C\\
\
\\
\
\int \dfrac{1}{\sqrt{1-x^2}} dx =\arcsin x+C\\
\
\\
\
\int \dfrac{1}{\sqrt{x^2-a^2}} dx =\ln|x+\sqrt{x^2-a^2}|+C\\
\
\\
\
\int \dfrac{1}{\sqrt{x^2+a^2}} dx =\ln|x+\sqrt{x^2+a^2}|+C
\]
三角函数公式：
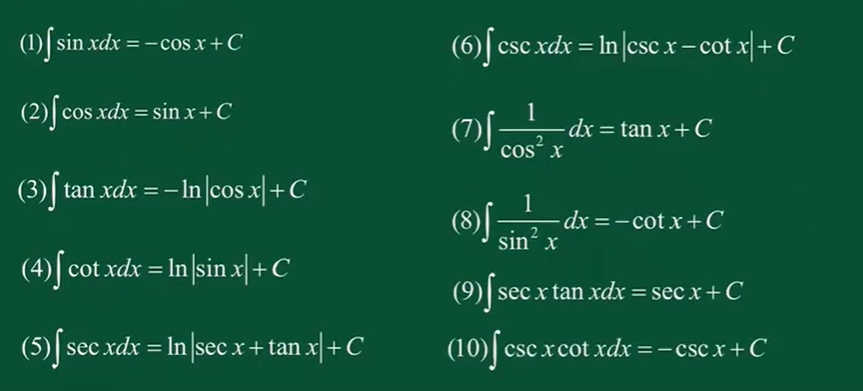
换元积分
设函数 \(f\) 在区间 \(I\) 上有定义，\(\varphi(x)\) 在区间 \(J\) 上可导，且 \(\varphi(J)\subseteq I\) 。
第一换元积分法：
若 \(\int f(x)dx=F(x)+C\) 在 \(I\) 上存在，则 \(\int f(\varphi(t))\varphi'(t)dt\) 在 \(J\) 上也存在，且：
\[\int f(\varphi(t))\varphi'(t)dt=F(\varphi(t))+C
\]
第二换元积分法：
若 \(x=\varphi(t)\) 存在反函数 \(t=\varphi^{-1}(x)\) ，且 \(\int f(\varphi(t))\varphi'(t)dt=G(t)+C\) ，则：
\[\int f(x)dx=G(\varphi^{-1}(x))+C
\]
分部积分法
若 \(u(x)\) 、\(v(x)\) 可导，且 \(\int u'(x)v(x)dx\) 存在，那么 \(\int u(x)v'(x)dx\) ，且：
\[\int u(x)v'(x)dx=u(x)v(x)-\int u'(x)v(x)dx
\]
常用于：
-
对数、指数、三角函数、反三角函数等与多项式的积。
-
三角函数与指数函数之积。
顺序：
三角函数、指数函数、幂函数、对数函数、反三角函数
例题：
（1）
\[\int \dfrac{dx}{a^2+x^2}\\
=\dfrac{1}{a^2}\int \dfrac{dx}{1+\frac{x^2}{a^2}}\\
=\dfrac{1}{a}\int \dfrac{d\dfrac{x}{a}}{1+\dfrac{x^2}{a^2}}\\
\]
而 \(\int \dfrac{1}{1+x^2}=\arctan x\)，则：
\[\int \dfrac{dx}{a^2+x^2}\\
=\dfrac{1}{a}\int \dfrac{d\dfrac{x}{a}}{1+\dfrac{x^2}{a^2}}\\
=\dfrac{1}{a}\arctan \dfrac{x}{a}
\]
（2）
\[\int \dfrac{\ln(1+\dfrac{1}{x})}{x(x+1)}dx\\
=\int \dfrac{1}{x^2}\dfrac{\ln(1+\dfrac{1}{x})}{(1+\dfrac{1}{x})}dx\\
\]
而 \(d(1+\dfrac{1}{x})=-\dfrac{1}{x^2}dx\)，即 \(dx=-x^2d(1+\dfrac{1}{x})\)，则：
\[\int \dfrac{\ln(1+\dfrac{1}{x})}{x(x+1)}dx\\
=\int \dfrac{1}{x^2}\dfrac{\ln(1+\dfrac{1}{x})}{(1+\dfrac{1}{x})}dx\\
=\int -\dfrac{x^2}{x^2}\dfrac{\ln(1+\dfrac{1}{x})}{(1+\dfrac{1}{x})}d(1+\dfrac{1}{x})\\
=-\int \dfrac{\ln(1+\dfrac{1}{x})}{(1+\dfrac{1}{x})}d(1+\dfrac{1}{x})
\]
令 \(t=1+\dfrac{1}{x}\) ，即：
\[\int \dfrac{\ln(t)}{t}dt\\
=\dfrac{1}{2}\ln^2(t)\\
=\dfrac{1}{2}\ln^2(1+\dfrac{1}{x})
\]
