虞皓翔构造题选讲
#3525. 「IOI2021」喷泉公园
给定平面上 \(n\) 个互不相同且坐标形如 \(\left(2 x_{i}, 2 y_{i}\right)\left(x_{i}, y_{i} \in \mathbb{Z}\right)\) 的点,每对距离为 \(2\) 的点之间连有一条边,保证所得的图 \(G\) 连通。
你需要构造 \(G\) 的一棵生成树 \(T=(V, E)\) ,同时构造 \(n-1\) 个形如 \(\left(2 x_{i}+1,2 y_{i}+1\right)\left(x_{i}, y_{i} \in \mathbb{Z}\right)\) 的点, 使得存在这些点到 \(E\) 的一一映射 \(\varphi\) 使得 \(p\) 和 \(\varphi(p)\) 的两端点构成等腰直角三角形。
\(1 ≤ n ≤ 2 × 10^5\) 。
solution
挑战哈密顿 2
给定无向简单图 \(G=(V, E)\) ,其中 \(V=\{(i, j) \mid 0 \leq i \leq C-1 , 0 \leq j \leq R-1\) 且 \(i, j\) 为整数 \(\}\),\(E\) 为所有距离为 \(1\) 或 \(\sqrt{2}\) 的点对构成的二元组。你需要找到 \(G\) 的一个 \(\text{Hamilton}\) 圈, 满足:
-
该圈的任意迭续两条边不平行 (等价地, 任意连续三点不共线);
-
(视每条边为直线段) 任意两条边不在非顶点处相交。
或说明其不存在。 \(R \times C \leq 10^{6}\) 。
Gym - 103495D Pattern Lock
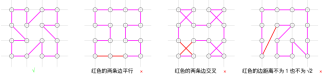
给定完全图 \(G=(V, E)\) ,其中 \(V=\{(i, j) \mid 0 \leq i \leq C-1 0 \leq j \leq R-1\) $且 \(i, j\) 为整数 \(\}\) 。你需要找到 \(G\) 的一个 \(\text{Hamilto}\) 圈,满足视每条边为直线段后:
-
对任意点 \(v \in V\) ,它关联的两条边构成一个锐角。
-
每一条边不能经过除端点外的其它顶点。 或说明其不存在。
\(R \times C \leq 10^{6}\) 。
Gym - 103470L Secret of Tianqiu Valley
有 \(n\) 盏灯排成一圈, 标号为 \(0,1, \ldots, n-1\) 。给定每盏灯的初始状态 (开或关),你可以进行若千次如下操作:
- 选择一盛关闭的灯 (设标号为 \(i\) ), 切换标号为 \(i-1, i, i+1\) 的灯的状态 (下标在 \(\bmod n\) 意义下)。
你需要在 \(2 n\) 次操作以内 (含) 将所有灯点亮或说明无法做 到。\(3 \leq n \leq 10^{5}\)
Gym - 102154C Quick sort
给定一个排列 \(\boldsymbol{p}=\left[p_{1}, p_{2}, \ldots, p_{n}\right]\) 。对奇偶性不同的整数 \(l, r (1 \leq l<r \leq n)\) ,定义操作 \(S(l, r)\) 为:
- 将 \(p_{l}, p_{l+1}, \ldots, p_{r}\) 重排为 \(p_{l+1}, p_{l+3}, \ldots, p_{r}, p_{l}, p_{l+2}, \ldots, p_{r-1}\) 。
你需要构造一种操作序列将 \(\boldsymbol{p}\) 排序。\(1 \leq n \leq 3000\) ,操作次数不超过 \(15000\) 。
CF1503F Balance the Cards
称一个由非零整数构成的序列 \(\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) 是“平衡的",当且仅当其 满足如下三者之一:
-
\(n=0\) 。
-
存在 \(1 \leq k<n\) 使得 \(\left[a_{1}, a_{2}, \ldots, a_{k}\right]\) 和 \(\left[a_{k+1}, a_{k+2}, \ldots, a_{n}\right]\) 都是“平衡的" 。
-
\(a_{1}=-a_{n}>0\) 且 \(\left[a_{2}, a_{3}, \ldots, a_{n-1}\right]\) 是“平衡的” 。
给定 \(2 n\) 个二元组 \(\left(u_{i}, v_{i}\right)\),保证 \(\left\{u_{1}, u_{2}, \ldots, u_{2 n}\right\}=\left\{v_{1}, v_{2}, \ldots, v_{2 n}\right\}= \{1,-1,2,-2, \ldots, n,-n\}\) ,你需要找到一个大小为 \(2 n\) 的排列 \(p_{1}, p_{2}, \ldots, p_{2 n}\) ,使得下列两个条件同时成立:
-
\(\left[u_{p_{1}}, u_{p_{2}}, \ldots, u_{p_{2 n}}\right]\) 是“平衡的”。
-
\(\left[v_{p_{1}}, v_{p_{2}}, \ldots, v_{p_{2_{n}}}\right]\) 是“平衡的”。
给出一组构造,或说明无解。\(1 \leq n \leq 2 \times 10^{5}\) 。
#702. 【SPC #3】最大生成掌
给定带权完全图 \(G=(V, E)\) ,其中 \(V=\{1,2, \ldots, n\}\) ,边 \((i, j)\) 的权值为 \(|i-j|\) ,求 \(G\) 的最大生成 (简单) 仙人掌的边权和,并给出一组构造。
\(1 \leq n \leq 5 \times 10^{5}\) 。
Jeopardy
考虑完全图 \(K_{16}=(V, E)\) ,其中 \(V=\{1,2, \ldots, 16\}\) ,你需要将 \(E\) 划分成 \(20\) 个大小为 \(6\) 的子集,使得每个子集是某个 \(K_{4}\) 的 \(6\) 条边 (即 \(K_{16}\) 的边 \(K_{4}\) 划分)。
进一步,其中某些子集是额先给出的,即你的划分中必须完整地包含这些子集。请给出一组构造或说明无解。
Gym - 102055C GCD Land
给定图 \(G=(V, E)\) ,其中 \(V=\mathbb{N}\),\(E=\{(i, j) \mid \operatorname{gcd}(i, j)>1\}\) 。给定 \(N\) ,求是否存在 \(X \in \mathbb{N}\) 满足 \(S_{X}=\{X, X+1, \ldots, X+N-1\}\) 导出的子图 \(G\left[S_{X}\right]\) 连通,若是,给出满足条件的 \(X\) 。
\(1\le N\le 10^5\) 。
CF329E Evil
坐标平面上有 \(n\) 个互不相同的点 \(p_{i}=\left(x_{i}, y_{i}\right)\) ,定义带权完全图 \(G=(V, E)\) ,其中 \(V=\left\{p_{1}, p_{2}, \ldots, p_{n}\right\}\) ,两点之间的权值为其 \(\text{Manhattan}\) 距离。求 \(G\) 的最长 \(\text{Hamilton}\) 圈的长度。
\(3\le n\le 10^5\) 。
JOISC 2017 Day4T2 City
这是一道通信题。
给定一棵 \(N\) 个顶点的有根树,保证所有顶点的深度 (到根的距离) 不超过 \(18\)。\(\text{Alice}\) 需要给每个顶点 \(v\) 进行编码 \(c_{v}\) ,需要满足 \(0 \leq c_{v} \leq 2^{28}-1\) 。
\(\text{Bob}\) 不知道关于这棵树的任何信息,而 \(\text{Bob}\) 需要回答若干次询问:每次询问 \(\text{Bob}\) 将收到顶点 \(x\),\(y(x \neq y)\) 的编码 \(c_{x}, c_{y}\) ,然后 \(\text{Bob}\) 需要判断以下三种情况哪一种成立:
-
\(y\) 是 \(x\) 的祖先。
-
\(x\) 是 \(y\) 的祖先。
-
\(x, y\) 不存在祖先关系。
\(2 \leq N \leq 2.5 \times 10^{5}\) 。
#3392. 「2020-2021 集训队作业」大鱼划水
坐标平面上有 \(n\) 个互不相同的点 \(\left(x_{i}, y_{i}\right)\) ,你需要在每个点上写一个 \(1 \sim n\) 之间的整数,并保证这些整数互不相同。
定义一条直线为 "好的",如果它满足如下三个条件:
-
平行于坐标轴 ( \(x\) 轴或 \(y\) 轴);
-
经过至少一个 (给定的) 点;
-
经过的所有点上所写的数的最大公约数为 \(1\)。
求 “好的" 直线的数量的最大值, 并给出一组构造。
\(1 \leq n \leq 2 \times 10^{5}\) 。
HDU - 7092 仓颉造数
给定正整数 \(a, b\) ,初始时 \(S \leftarrow\left\{\frac{a}{b}, \frac{b}{a}\right\}\) 。你可以进行若干次如下操作:
- 选择 \(S\) 中两个数 \(x, y\) ,令 \(S \leftarrow S \cup\left\{\frac{x+y}{2}, \frac{2 x y}{x+y}\right\}\) 。
求是否可以在有限步内使 \(1 \in S\) 。\(1 \leq a, b \leq 10^{9}\) 。
#712. 【SPC #3】同构判定海蜇
给定一个群 \((S , o)\),你需要构造一张无向简单图 \(G=(V, E)\) 满足它的自同构群 \(\text{Aut} G \cong S\) , 且 \(|V| \leq 127\) 。
\(1 \leq|S| \leq 63\) 。


