代晨昕杂题选讲

#3523. 「IOI2021」分糖果

直接处理不太好做，发现我们只需求最终结果，考虑将序列当作询问做扫描线，线段树维护与当前位置有关的操作。

维护每个区间内变化量前缀和的最大最小值，发现如果一个区间最大值与最小值只差超过了 \(c[i]\) ，那么在这个区间内至少会碰到一次顶部或底部，触碰边界前的操作就不重要了。

令 \(\text{solve}(\text{x,lim,l,r})\) 表示初始值为 \(x\) ，上限为 \(\text{lim}\) ，经历了 \([l,r]\) 这段区间的操作后会变成多少。

如果当前节点的右区间最大值与最小值只差超过了 \(\text{lim}\) ，那么左区间的操作就是没用的，可以直接递归进 \(\text{solve}(\text{x,lim,mid+1,r})\) 。

否则无论经历左区间后 \(x\) 为多少，经历右区间时最多只会触碰上边界或下边界其中一个，可以直接通过 \(\text{solve}(\text{x,lim,l,mid})\) 分类讨论出来。

点击查看代码

#3524. 「IOI2021」钥匙

要求 \(p[i]\) 最小的点，如果一个点能走到另一个点，另一个点却走不回这个点，那么这个点一定不如另一个点优。

考虑对每个点维护能走到它的集合，每次扩展时走如果遇到自己集合内的点则正常扩展，如果遇到了一个没有包含在自己集合中的点，无论这个点能否走到自己，自己所在集合内的点一定能走到这个点，将自己所在的集合合并给这个点即可。

这样暴力做可能是 \(O(n^2)\) 的，我们可以每轮每个集合只访问一次，容易发现每轮每个可以和别的集合合并的集合至少会和一个集合合并，类似 \(\text{Boruvka}\) 算法，这个过程只会进行 \(\log n\) 轮。

点击查看代码

[CERC2013]History course

把区间按照右端点从小到大排序，令 \([a_i,b_i]\) 表示排好序后第i个区间的端点。此时，两个区间 \(i,j(i<j)\) 相交当且仅当 \(a_j\le b_i\)

直接解决原问题十分困难，考虑先二分答案 \(k\)，转化为判断答案能否 \(\le k\) 的判定问题。

考虑从左到右构造答案序列。假设我们已经确定了最优序列的前 \(id-1\) 位，现在我们要考虑第 \(id\) 位。

这时，待定区间 \(i\) 可能会和某些位于前 \(id-1\) 位的区间相交，因此有在序列中的位置的上限 \(lim[i]\)，若没有限制则 \(lim[i]=n\) 。

感性理解一下，我们应该希望当前选定的区间的右端点尽可能小，这样对 \(lim\) 数组的影响也尽可能小。

令 $cnt[i] $表示 \(lim=i\) 的区间的个数，\(pre[id-1]=0,pre[i]=pre[i-1]+1-cnt[i](i\ge id)\)

如果我们钦定区间 \(x\) 填在第 \(id\) 位，答案存在的必要条件为将 \(lim[x]\) 改为 \(id\) 后，\(pre\) 数组恒大于等于 \(0\) 。

考虑 \(lim[x]\) 更改之前。如果 \(cnt[id]>1\)，则显然无解；如果 \(cnt[id]=1\)，则这一位已经确定。

如果 \(cnt[id]=0\)，则将 \(x\) 填在第 \(id\) 位时答案存在的必要条件为 对所有 \(id\le i<lim[x],pre[i]>0\) 。

找到所有满足此条件的 \(x\) 中右端点最小的一个，考虑用线段树维护 \(cnt[i]\)，寻找 \(x\) 可以在线段树上二分来完成。确定 \(x\) 填在第 \(id\) 位后，找到所有需要更改 \(lim\) 的区间，并在线段树上单点修改。

每次二分需要花费 \(O(n\log n)\) 的时间，所以可以在 \(O(n\log^2n)\) 的时间内解决本题。

点击查看代码

[ICPC2018 WF]Gem Island

先看看对于一种最终状态 \(a_1, a_2, \ldots, a_n\) ，其发生的方案数，我们可以分成两个部分：

第一步是将 \(d\) 天分给 \(n\) 个人，钦点这 \(d\) 天是谁手上的宝石数增加了：

\[\prod_{i=1}^{n}\binom{d-\sum_{j=1}^{i-1}(a_j-1)}{a_i-1}=\frac{d!}{\prod_{i=1}^{n}(a_i-1)!} \]

第二步是对于每一天，计算当天被钦定的人手上宝石数增加的方案数；事实上，在一个人手上的宝石第 \(i\) 次增加 \(1\) 的时候，这时候发生这种情况的方案数就一定是 \(i\) 种。则将 \(n\) 个人的方案数都乘起来，则可以认为是：

\[\prod_{i=1}^{n}(a_i-1)! \]

将两个部分乘起来，则我们可以得到一个令人兴奋的结论：对于任何一种最终状态，它发生的方案数都是 \(d!\)。这也就意味着，所有的最终状态发生的概率都是相等的！

那么我们就可以直接 \(dp\) 所有方案数以及这些方案的前 \(r\) 大的 \(a_i\) 的和就行了。

考虑一种经典的“搭楼梯”的 \(dp\) 方法：

我们维护类似这样一个“楼梯”状的东西：

***
******
******
********
********
********
**********
**********

考虑设 \(f_{i,j}\) 表示当前最高的“楼梯”有 \(i\) 列，“楼梯”里头 \(*\) 的总数为 \(j\) 的方案数。上面这个东西就是 \(f_{3,59}\) 的一种方案。

转移很简单，考虑在最高层加入一行，枚举这行里头有 \(k\) 个 \(*\)，然后从现有的 \(j\) 列里头选 \(k\) 列放到最左边，然后在这 \(k\) 行上面各加上一个 \(*\) 就是一种转移了。比如对上面的 \(f_{3,59}\) ，枚举 \(k=2\) 的时候可以转移到 \(f_{2,61}\) ，其转移系数为 \(\binom{3}{2}\)。转移之后的形态可以这么表示：

**          <--- 新增的行
***
******
******
********
********
********
**********
**********

将这个东西放到这个题中，我们可以将宝石对应成 \(*\)，每一列对应一个人就行了。

然后考虑计算所有方案的前 \(r\) 大的 \(a_i\) 的和。转化成上面的东西就变成了前 \(r\) 列的 \(*\) 的和。事实上也很简单，由于我们每次加入一行的那些列，一定就是前 \(k\) 大的列，而且每列都只加入了一个 \(*\)，所以我们可以直接计算贡献。具体来说，我们类比 \(f_{i,j}\) 设 \(g_{i,j}\) 为当前维护前 \(i\) 大，一共有 \(j\) 个宝石的所有方案的前 \(r\) 大的数的和。那么转移就可以写成：

\[g_{i,j}=\sum_{k=i}^{\min(n,i)}(g_{k,j-i}+\min(i, r) \times f_{k,j-i})\times \binom{k}{i} \]

最后答案也很显然，就是

\[\frac{\sum_{i=1}^{n}g_{i,d}}{\sum_{i=1}^{n}f_{i,d}} \]

了。

点击查看代码

XXI Opencup GP of Tokyo Count Min Ratio

[CCO2021] Travelling Merchant

容易得到 \(dp\) 方程：\(dp[x]=\min_{x\to u}\max(dp[u]-p[i],r[i])\) 。

但是图是有环的，不能直接这样做，考虑剥去叶子，对于当前 \(r[i]\) 最大的边，由于 \(u\) 在环上，一定有 \(dp[u]\le r[i]\) ，因此我们可以直接用 \(r[i]\) 去更新 \(dp[x]\) 并将这条边删掉，然后可能会产生新的叶子，剥除后继续删最大边即可。

点击查看代码

WF2014 H Pachinko

设 \(ans[i][j]\) 表示经过 \((i,j)\) 这个格子的期望次数，由于经过靶子就会立刻停下，这个期望就是我们要求的答案。

根据题目条件可以简单列出 \(wh\) 个方程，这个题目有障碍的存在，所以不能取一行当主元，高斯消元矩阵的有效部分大概长这样。

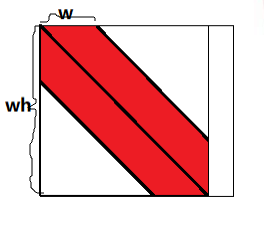
先将其消成上三角矩阵，注意到每次消元时只会影响前后 \(m\) 个方程，故只保存增广矩阵中的这些项，同时只对这些项进行消元即可。

时间复杂度 \(O(nm^3)\) 。

点击查看代码

[ICPC2019 WF]Traffic Blights

转化为求通过前 \(i\) 个红绿灯的概率，即相当于求满足若干形如 \(x \not \equiv a \pmod {r_i+g_i}\) 限制的 \(x\) 的方案数。

记 \(m_i = r_i + g_i\) ，则整条街的周期是 \(\operatorname{lcm}(m_1,m_2,\cdots, m_n)\) 。

考虑一个简单的问题，若 \(m_i\) 两两互质，则任取 \(x \equiv a \pmod {m_i}\)，\(x \equiv b \pmod {m_j}\)，总有唯一的 \(\bmod \operatorname{lcm}(m_i,m_j)\) 意义下的解，故所有 \(m_i\) 的概率互相独立。

考虑假如任取 \(m_i,m_j\) 要么互质，要么其中一个是另外一个的倍数，则可以把 \(m_i\) 分为若干个互相独立的类，对于一类的 \(m_i\) ，考虑暴力将其变成最大的 \(m_i\) 中的若干段区间，然后暴力维护，这样就可以做到 \(\mathcal O(n \max m_i)\) 的复杂度。

考虑一般的情况如何转化为以上的情况，我们枚举出发时间 \(\bmod\) 某个提前设定好的正整数 \(M\) 的值 \(c\)。

之后新的时间 \(t\) 对应这原来的时间 \(c+t\cdot M\)，则原先每个红绿灯的周期 \(m_i\) 变为 \(\dfrac {\operatorname{lcm}(M,m_i)}{M} = \dfrac {m_i}{\gcd(M,m_i)}\) 。

假如我们让所有 \(\dfrac {m_i}{\gcd(M,m_i)}\) 要么两两互质，要么是倍数关系，我们就可以算了。考虑这样的情况必然除完之后是 \(1\) 或质数的次幂。可算得最小的 \(M = 2^3\times 3^2\times 5\times 7 = 2520\) 。

时间复杂度 \(\mathcal O(Mn \max m_i)\) 。

点击查看代码