欧拉回路的判定与构造
欧拉回路的判定
(有向图/无向图的)欧拉路径是一条路径,满足其经过所有边恰好一次。欧拉回路是起点和终点相同的一条欧拉路径。欧拉通路是起点和终点不同的一条欧拉路径。
有向图存在欧拉回路:将边看成无向边后图联通,且所有点入度均等于出度。
有向图存在欧拉通路:将边看成无向边后图联通,且除两个点外,所有点入度均等于出度。那两个点中,其中一个出度比入度大 \(1\),作为欧拉通路的起点。另一个入度比出度大 \(1\),作为欧拉通路的终点。
无向图存在欧拉回路:所有点度数均为偶数。
无向图存在欧拉通路:除两个点度数为奇数外,所有点度数均为偶数。那两个点中,一个作为欧拉通路之起点,另一个作为终点。
[AGC032C] Three Circuits
有一张 \(n\) 个点 \(m\) 条边的简单无向连通图。
请你判断能否将边分成三个集合,每个集合都是一个可以多次经过重复点的环。
\(1 \leq n, m \leq 10^5\) 。
solution
由于三环并集包含整个图,所以该图必有欧拉回路。
对点的度数进行讨论:
-
有一点度数大于等于 \(6\),从这个点至少可以拆出三个环,合法。
-
所有点度数小于等于 \(2\),整个图就是一个环,不合法。
-
除去前两种情况的图点的度数只能为 \(2/4\),度数为 \(2\) 的仅能在一个环中,于是至少有两个度数为 \(4\) 的点,而且这两个点拆出的两条回路不完全相同,才能合法。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int vi[100005];
vector<int> e[100005];
int f1,f2;
void dfs(int x){
vi[x]=1;
for(auto u:e[x]){
if(vi[u]==2){
if(f1)f2=u;
else f1=u;
}
else if(!vi[u])dfs(u);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;scanf("%d%d",&x,&y);
e[x].push_back(y);e[y].push_back(x);
}
int maxx=0,k=0;
for(int i=1;i<=n;i++){
if(e[i].size()&1){
puts("No");
return 0;
}
if(e[i].size()>maxx)maxx=e[i].size(),k=1;
else k+=(maxx==e[i].size());
}
if(maxx>=6){
puts("Yes");
return 0;
}
if(maxx==2||k==1){
puts("No");
return 0;
}
if(k>2){
puts("Yes");
return 0;
}
for(int i=1;i<=n;i++){
if(e[i].size()==4)vi[i]=2;
}
for(int i=1;i<=n;i++){
if(!vi[i]){
f1=f2=0;dfs(i);
if(f1==f2){
puts("Yes");
return 0;
}
}
}
puts("No");
return 0;
}
[AGC017E] Jigsaw
给定 \(n\) 块积木,每块积木由三个矩形组成,中间的矩形最高高度为 \(h_i\),左边的矩形高度为 \(a_i\) 离底边高度为 \(c_i\),右边的矩形高度为 \(b_i\) 离底边高度为 \(d_i\),现在要求将这些积木全部拼起来,并且中间部分的底边贴底,每个积木的左边和右边矩形的底边必须完全贴底或者完全贴在别的积木上,积木无法旋转或翻转,问是否存在合法的摆放方案。
solution
我们可以将积木看成边,对于每一个高度建两个点(称为正点(\(P(x)\))和负点(\(N(x)\)))。对于一个拼接处,属于右边的那块对应的是正点,属于左边的那块对应的是负点,具体高度的话就是拼接处的高度,举个例子:
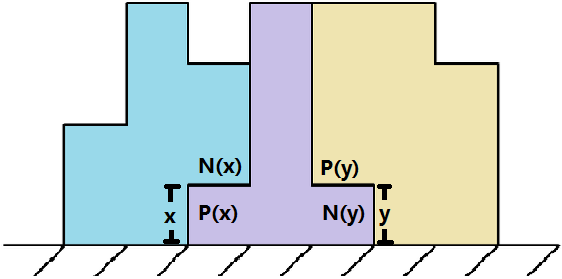
然后这样一来,连边的话就是对于每个积木,左边矩形对应的点向右边矩形对应的点连一条有向边,在上面这幅图来看的话就是 \(P(x)\to N(x)\),那么现在我们的问题就变成了要在这个有向图中找若干条从正点开始在负点结束的路径,使得所有边都被经过一次(因为一条边对应一个积木)。
我们新搞一个超级源之类的点,如果说一个图存在一条这样的路径,那么我们从超级源向这条路径的起点连边,从终点再连一条有向边到超级源,那么我们可以得到一条回路,如果说整个图存在满足上述的“所有边都被经过一次”的划分,那么说明整个图(算上超级源)一定弱连通并且存在欧拉回路,具体构造的话就是。。每次从超级源出发走一条这样的路径回来,重复直到所有的边都经过了一次,这个时候将所有连着超级源的边都删掉就是一种合法的划分了
那么现在要做的就是判断是否存在欧拉回路了。
一个弱连通图如果要存在欧拉回路,必须满足每个点的入度和出度相等,那么我们就首先可以得到两个限制条件:
(1)对于所有的正点,\(in[i]\le out[i]\)(之所以是是因为超级源会向路径起点连一条边,那么路径起点的入度会,而我们的回路是放在整个包含超级源的图里面看的,所以是 \(\le\) )
(2)对于所有的负点,\(in[i]\ge out[i]\)(类似地,终点要向超级源连边所以出度会要 \(+1\) )
有了这两个条件之后还有一个问题,就是我们并不能保证整个图连通,再具体一点就是我们会漏掉一个弱连通块满足这个弱连通块中的每一个点入度都和出度相等这种情况,这种情况没有办法通过起点终点与超级源连边的方式构造出欧拉回路(因为要求起点和终点一正一负,所以连了边之后起点和终点的出度和入度必定不相等),所以一旦出现这种情况肯定是无解的,否则的话就一定能按照上面说的构造方式构造出一种划分。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define P(x) (x)
#define N(x) (x+h)
int dsu[200005],outd[200005],ind[200005],ok[200005];
int n,h;
int find(int x){
return dsu[x]==x?x:dsu[x]=find(dsu[x]);
}
inline void link(int x,int y){
x=find(x);y=find(y);
dsu[x]=y;
}
inline bool solve(){
for(int i=P(1);i<=P(h);i++)if(ind[i]>outd[i])return 0;
for(int i=N(1);i<=N(h);i++)if(ind[i]<outd[i])return 0;
for(int i=P(1);i<=N(h);i++)if(ind[i]!=outd[i])ok[find(i)]=1;
for(int i=P(1);i<=N(h);i++)if(!ok[find(i)]&&(ind[i]||outd[i]))return 0;
return 10;
}
int main(){
scanf("%d%d",&n,&h);
for(int i=P(1);i<=N(h);i++)dsu[i]=i;
for(int i=1;i<=n;i++){
int a,b,c,d;scanf("%d%d%d%d",&a,&b,&c,&d);
int l=c?N(c):P(a),r=d?P(d):N(b);
link(l,r);
++outd[l];++ind[r];
}
if(solve())puts("YES");
else puts("NO");
return 0;
}
[NOI2021SDPTTest4]度数
给定一张 \(n\) 个点 \(m\) 条边的无向连通图,可能有重边,但没有自环。
你需要给每条边确定方向,变成有向图。这个有向图需要满足这些条件:
对于编号为 \(i\) 的结点 \((1\leq i\leq n)\),\(\operatorname{indeg}(i)\geq x_i\) 。
对于编号为 \(i\) 的结点 \((1\leq i\leq n)\),\(\operatorname{outdeg}(i)\geq y_i\) 。
其中 \(x_i,y_i\) 都是提前给定的,\(\operatorname{indeg}(i)\) 表示点 \(i\) 的入度,\(\operatorname{outdeg}(i)\) 表示点 \(i\) 的出度。
如果存在方案,请求出任意一种,否则声称不存在合法方案。
\(2≤n≤5×10^5,1≤m≤5×10^5,0≤x_i,y_i≤1\) 。
solution
发现 \(0≤x_i,y_i≤1\) ,那么如果一个点既有入度又有出度,那么就一定合法,考虑把原图补成欧拉图,然后跑欧拉回路,这样对于所有原来度数大于 \(2\) 的点至少在原图中各有一条入边和出边。但是对于度数为 \(1\) 的点,入边和出边中至少有一条边是后加的,容易发现,对于这种点,它在原图中那一条边的方向是确定的,拓扑排序删叶子,把这类点去掉即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
bool vis[500005][2];
int ver[4000005],ne[4000005],head[500005],cnt=1,deg[500005];
int ans[4000005];
inline void link(int x,int y){
ver[++cnt]=y;
ne[cnt]=head[x];
head[x]=cnt;deg[y]++;
}
queue<int> q;
void dfs(int x){
for(int &i=head[x];i;i=ne[i]){
int u=ver[i];
if(~ans[i>>1])continue;
deg[x]--;deg[u]--;//cout<<x<<"->"<<u<<endl;
ans[i>>1]=(i&1);dfs(u);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);vis[i][0]=x;
}
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);vis[i][1]=x;
}
for(int i=1;i<=m;i++){
int x,y;scanf("%d%d",&x,&y);
link(y,x);link(x,y);
}
memset(ans,-1,sizeof(ans));
for(int i=1;i<=n;i++){
if(!deg[i]&&(vis[i][0]||vis[i][1])){
puts("-1");
return 0;
}
if(deg[i]==1&&(vis[i][0]||vis[i][1]))q.push(i);
}
while(!q.empty()){
int x=q.front();q.pop();
if(vis[x][0]&&vis[x][1]){
puts("-1");
return 0;
}
for(int i=head[x];i;i=ne[i]){
if(~ans[i>>1])continue;
int u=ver[i];
if(vis[x][0]){
ans[i>>1]=((i&1)^1);
vis[x][0]=vis[u][1]=0;
}
else if(vis[x][1]){
ans[i>>1]=(i&1);
vis[x][1]=vis[u][0]=0;
}
--deg[x];
if(--deg[u]==1&&(vis[u][0]||vis[u][1]))q.push(u);
}
}
for(int i=1;i<=n;i++){
if(!deg[i]&&(vis[i][0]||vis[i][1])){
puts("-1");
return 0;
}
}
for(int i=1;i<=n;i++)if(deg[i]&1)link(0,i),link(i,0);
for(int i=1;i<=n;i++)while(deg[i])dfs(i);
for(int i=1;i<=m;i++)printf("%d ",ans[i]);
return 0;
}
欧拉回路的构造
构造欧拉回路可以直接 \(\text{dfs}\),具体来说,我们不断找环,用栈合并即可。
无向图欧拉回路:
void dfs(int x){
vis[x]=1;
for(int &i=head[x];i;i=ne[i]){
if(~ans[i>>1])continue;
int u=ver[i];
ans[i>>1]=(i&1);dfs(u);
}
}
有向图欧拉回路:
void dfs(int x){
for(int &i=head[x];i;i=ne[i]){
if(vis[i])continue;vis[i]=1;
int u=ver[i];
dfs(u);ans.push_back(make_pair(x,u));
}
}
CF547D Mike and Fish
给定 \(n\) 个整点,你要给每个点染成红色或蓝色。
要求同一水平线或垂直线上两种颜色的数量最多相差 \(1\)。
\(n,x_i, y_i \le 2 \times 10^5\) 。
solution
我们首先将点的染色对应为赋值为 \(1\) 或 \(-1\)。那么限制对应为每行每列的和为 \(0,1\) 或 \(-1\) 。
我们将行列均建成点,称第 \(i\) 行对应的点为 \(col(i)\) ,第 \(i\) 列对应的点是 \(rol(i)\) 。将平面上的点 \((x,y)\) 对应为双向边 \((col(x),rol(y))\) 。考察若原图有一欧拉回路,则可使每行每列均为 \(0\)。
具体来说,考察每条边是被正向还是被反向经过来定对应的点的权值为 \(-1\) 或 \(1\) ,由于欧拉回路是环套环结构所以每个新图中的点的出入次数相同,也即和为 \(0\) 。
考虑给图加上一些边使得加完边后的图有欧拉回路,如果没有两条边被加在同一个点上那么去掉这些新加的边的贡献后必然有每个点被出入的次数差的绝对值在 \(1\) 以内,也即合法。
我们考虑所有入度和出度奇偶性不相等的点,在它们间每对加边即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> le[200005],ri[200005];
vector<int> vec[200005];
int ans[200005];
void dfs(int x,int op){
if(ans[x])return ;
ans[x]=op;
for(auto u:vec[x])dfs(u,-op);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x,y;scanf("%d%d",&x,&y);
le[x].push_back(i);ri[y].push_back(i);
}
for(int i=1;i<=2e5;i++){
int pre=0;
for(auto it:le[i]){
if(!pre)pre=it;
else {
vec[pre].push_back(it);
vec[it].push_back(pre);pre=0;
}
}
}
for(int i=1;i<=2e5;i++){
int pre=0;
for(auto it:ri[i]){
if(!pre)pre=it;
else {
vec[pre].push_back(it);
vec[it].push_back(pre);pre=0;
}
}
}
for(int i=1;i<=n;i++)dfs(i,1);
for(int i=1;i<=n;i++)printf("%c",~ans[i]?'b':'r');
return 0;
}
CF527E Data Center Drama
给定一张 \(n\) 个点 \(m\) 条边的连通无向图。
你需要加尽可能少的边,然后给所有边定向,使得每一个点的出入度都是偶数。
\(n \le 10^5\),\(m \le 2 \times 10^5\)。
solution
将度数为奇数的点匹配,如果总边数为奇数,再加一个自环,跑欧拉回路,欧拉回路中每个点入度等于出度,隔位取反即可保证出入度均为偶数。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int ver[4000005],ne[4000005],head[4000005],cnt=1,du[4000005];
inline void link(int x,int y){
ver[++cnt]=y;
ne[cnt]=head[x];
head[x]=cnt;du[y]++;
}
bool vis[4000005];
bool is=0;
void dfs(int x){
for(int &i=head[x];i;i=ne[i]){
int u=ver[i];
if(vis[i])continue;
vis[i]=vis[i^1]=1;
dfs(u);
if(is^=1)printf("%d %d\n",x,u);
else printf("%d %d\n",u,x);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;scanf("%d%d",&x,&y);
link(x,y);link(y,x);
}
for(int i=1,j=2;i<=n;i++){
if(du[i]&1){
while(j==i||(du[j]&1)==0)j++;
link(i,j);link(j,i);
}
}if(cnt&2)link(1,1),link(1,1);
printf("%d\n",cnt/2);
dfs(1);
return 0;
}
CF429E Points and Segments
给定 \(n\) 条线段 \([l_i,r_i]\),然后给这些线段红蓝染色,使得直线上上任意一个点被蓝色及红色线段覆盖次数之差的绝对值不大于 \(1\) 。
solution
将红色线段视为区间加一,蓝色视为区间减一,考虑差分,变为红色线段 \(l_i\) 加一,\(r_i+1\) 减一,蓝色线段 \(l_i\) 减一,\(r_i+1\) 加一。
如果题目要求每个点红蓝色数量相等,那么要求差分数组全 \(0\) ,连双向边 \((l_i,r_i+1)\) 跑欧拉回路即可。题目要求每个点相差不超过 \(1\) ,只需对每个被覆盖了奇数次的点 \(i\),加一个区间 \([i,i]\) 即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
int L[100005],R[100005];
int ver[600005],ne[600005],head[200005],cnt=1,deg[200005];
inline void link(int x,int y){
ver[++cnt]=y;
ne[cnt]=head[x];
head[x]=cnt;++deg[y];
}
vector<int> hsh;
int ans[300005];
bool vis[300005];
void dfs(int x){
vis[x]=1;
for(int &i=head[x];i;i=ne[i]){
if(~ans[i>>1])continue;
int u=ver[i];
ans[i>>1]=(i&1);dfs(u);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d%d",&L[i],&R[i]),R[i]++;
for(int i=1;i<=n;i++)hsh.push_back(L[i]);
for(int i=1;i<=n;i++)hsh.push_back(R[i]);
sort(hsh.begin(),hsh.end());
hsh.erase(unique(hsh.begin(),hsh.end()),hsh.end());
for(int i=1;i<=n;i++)L[i]=upper_bound(hsh.begin(),hsh.end(),L[i])-hsh.begin();
for(int i=1;i<=n;i++)R[i]=upper_bound(hsh.begin(),hsh.end(),R[i])-hsh.begin();
for(int i=1;i<=n;i++){
link(L[i],R[i]);
link(R[i],L[i]);
}
for(int i=1;i<hsh.size();i++){
if(deg[i]&1){
link(i,i+1);
link(i+1,i);
}
}
for(int i=1;i<=cnt/2;i++)ans[i]=-1;
for(int i=1;i<=hsh.size();i++)if(!vis[i])dfs(i);
for(int i=1;i<=n;i++)printf("%d ",ans[i]);
return 0;
}
[AGC018F] Two Trees
给定两棵都是 \(n\) 个节点的有根树 \(A,B\),节点均从 \(1..n\) 标号。
我们需要给每个标号定一个权值,使在两棵树上均满足任意节点子树权值和为 \(1\) 或 \(-1\) 。
输出任意一种解,需要判断无解。\(n\leqslant 100000\) 。
solution
首先可以发现,对于任意一组和法解,一定存在一种方式使得每个点的点权 \(\in(-1,0,1)\) 。对于一个点 \(i\) ,设其点权为 \(a_i> 1\) ,由于这个点的子树和不超过 \(1\) ,它儿子的子树和又都 \(\in(-1,1)\) ,那么它至少有一个儿子子树和为 \(-1\) ,将整棵子树的权值取反,同时将点 \(i\) 的权值减 \(2\) ,仍然是一种合法方案。可以不断重复这样的操作,直到每个点的点权都 \(\in(-1,0,1)\) 为止。
只考虑 \(-1\) 和 \(1\) 情况,容易想到保留两棵树的边,并将两棵树的父亲与一个虚点连边,再将两棵树对应点连边,跑欧拉回路定向,对于某一棵树而言,如果它与它父亲的边是向外的,说明它子树内由另一棵树指向这棵树的点恰好比这棵树指向另一棵树的点多一个,否则恰好少一个。只要按边的方向确定 \(-1\) 或 \(1\) ,就能达到任意节点子树和 \(\in(-1,1)\) 的效果。
不过这样建图不一定能保证存在欧拉回路,如果一个点的度数是奇数,那么去掉它和对应点的连边,以及它和父亲的连边,剩下它的儿子,容易发现它的儿子数一定是奇数。这些儿子的子树和都 \(\in(-1,1)\),想让这个点的子树和 \(\in(-1,1)\),这个点的权值只能是 \(0\) ,对于这种点,不和对应点连边即可。
如果一个点在一棵树中权值必须是 \(0\) ,另一棵树不是,那么这个问题无解,特判掉即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,rt1,rt2;
vector<int> vec[200005];
bool deg[200005];
void init(int x){
deg[x]=1;
for(auto u:vec[x]){
init(u);deg[x]^=1;
}
}
int ver[600005],ne[600005],head[200005],cnt=1;
inline void link(int x,int y){
ver[++cnt]=y;
ne[cnt]=head[x];
head[x]=cnt;
}
int dir[300005],ans[100005];
void dfs(int x){
for(int &i=head[x];i;i=ne[i]){
if(~dir[i>>1])continue;
int u=ver[i];
dir[i>>1]=(i&1);dfs(u);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
if(~x)vec[x].push_back(i);
else rt1=i;
}
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
if(~x)vec[x+n].push_back(i+n);
else rt2=i+n;
}
init(rt1);init(rt2);
for(int i=1;i<=n;i++)if(deg[i]!=deg[i+n]){
puts("IMPOSSIBLE");
return 0;
}
for(int i=1;i<=n;i++)if(deg[i]){
link(i,i+n);link(i+n,i);
ans[i]=cnt/2;
}
for(int i=1;i<=n;i++){
for(auto u:vec[i]){
link(i,u);link(u,i);
}
for(auto u:vec[i+n]){
link(i+n,u);link(u,i+n);
}
}
link(2*n+1,rt1);link(rt1,2*n+1);
link(2*n+1,rt2);link(rt2,2*n+1);
for(int i=1;i<=cnt/2;i++)dir[i]=-1;
dfs(1);
puts("POSSIBLE");
for(int i=1;i<=n;i++){
if(!deg[i])printf("0 ");
else printf("%d ",dir[ans[i]]?1:-1);
}
return 0;
}
#670. 【UNR #5】获奖名单
一共有 \(n\) 个外星蜜蜂,有 \(m\) 种符号。用这种语言表达每只外星蜜蜂的名字要么只需要一个符号,要么只需要两个符号。
你需要给这一批选手编写一份由他们所有人名字组成的获奖名单,再按顺序念出来。你可以做如下调整:
-
你可以调整这 \(n\) 个名字的排列顺序;
-
由于外星蜜蜂的特殊文化,所有两个符号的名字无论你顺着念还是倒着念,指代的都是同一只蜜蜂。所以名单中每个两个符号的名字你既可以按顺序写也可以按逆序写。
-
可能存在名字相同的多只蜜蜂,但你仍然要读这个名字多次。
为了避免倾向性,你希望最后把名字顺次连起来是个回文串。也就是说,你要让名字串起来后的符号序列从左到右读和从右往左读没有区别。
测试数据保证有解。
solution
记 \(L=\sum l_i\)。先手玩一下 \(L\) 是偶数的情况,方便起见先假设最终间两个字符不属于同一个名字,那么最终间两个字符旁边的字符属于的名字的情况只可能有以下三种:
-
两边都属于长度为 \(1\) 的名字:即 \([a]|[a]\) 的情况。
-
两边都属于长度为 \(2\) 的名字:即 \([ab]|[ba]\) 的情况。
-
一边属于长度为 \(1\) 的名字,一边属于长度为 \(2\) 的名字,不妨假设长度为 \(1\) 的名字在左边且为 \(a\),那么右边的名字必然带 \(a\),另一个设为 \(b\),而左边必然有一个名字与 \(b\) 匹配,又可以分长度为 \(1\) 和 \(2\) 讨论,如果是 \(1\) 那么必须为 \(b\),即 \([b][a]|[ab]\),我们把这些组删掉之后似乎又归纳变为了新的 \(L\) 是偶数的情况。而如果长度是 \(2\) 则 \(b\) 也必须跟一个字符搭配,设为 \(c\),而根据右边 \(c\) 所在名字长度有课分类讨论,以此类推下去,最终必然有一步会出现长度为 \(1\) 的名字,即 \([?!]…[ed][cb][a]|[ab][cd][ef]…[?]\) 。
如果我们建一个虚点并从所有孤立点向这个虚点连无向边,那么前两类可以视作删去一对重边,最后一类可以视作删去一个包含这个虚点的环。我们先假设存在一组解使得中间两个字符不属于同一个名字,考虑如何构造之,由于第三种情况必然包含这个虚点,因此图中与这个虚点不在同一连通块的部分必然只由一对对重边构成,它们的处理是容易的,我们可以暂时先扔了他们。而虚点所在的连通块必然是一张欧拉图,直接跑出一个欧拉回路然后将这个环一次性删除即可。
如果中间两个字符 \(\frac{L}{2},\frac{L}{2}+1\) 属于同一名字,那么处理方法也是类似的:相较于前者只是多添了一个自环而已,因此我们可以直接找出这个多余的自环然后一次操作带走它即可。
这样我们就完美地解决了 \(L\) 是偶数的情况,至于 \(L\) 是奇数时,发现相当于虚点所在的连通块中多了虚点和某个其他的奇度点,直接把这个奇度点找到然后跑欧拉路径即可。
时间复杂度 \(O(n+m)\) 。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n,m,S;
int ver[1000005],ne[1000005],head[500005],tot=1;
inline void link(int x,int y){
ver[++tot]=y;
ne[tot]=head[x];
head[x]=tot;
}
int deg[500005],a[500005],cnt;
int clk[500005],T;
bool flag[1000005],vis[500005];
vector<int> res[500005];
void dfs(int x,int id){
vis[x]=1;
for(int &i=head[x];i;i=ne[i]){
if(flag[i]||flag[i^1])continue;
int u=ver[i];
flag[i]=flag[i^1]=1;
dfs(u,i);
}
a[++cnt]=id;
}
int main(){
scanf("%d%d",&n,&m);
S=m+1;int L=0;
for(int i=1;i<=n;i++){
int op;scanf("%d",&op);
L+=op;
if(op==1){
int x;scanf("%d",&x);
deg[x]++;
link(S,x);link(x,S);
}
else{
int x,y;scanf("%d%d",&x,&y);
deg[x]++,deg[y]++;
link(x,y);link(y,x);
}
}
for(int i=1;i<=m;i++){
if(deg[i]&1){
link(S,i);link(i,S);
}
}
dfs(S,0);reverse(a+1,a+cnt+1);
vector<pair<int,int> > vec[2];
int now=0;
for(int i=1;i<=cnt;i++){
int id=a[i]>>1,tp=a[i]&1;
if(!id||id>n)continue;
now^=1;
vec[now].push_back(make_pair(id,tp));
}
int rt=0;
for(int x=1;x<=m;x++){
if(vis[x])continue;
T++;
vector<int> ve;
for(int i=head[x];i;i=ne[i]){
if(flag[i]||flag[i^1])continue;
flag[i]=flag[i^1]=1;
int u=ver[i];
if(clk[u]!=T)clk[u]=T,ve.push_back(u);
res[u].push_back(i);
}
for(int i=0;i<ve.size();i++){
int v=ve[i];
if(res[v].size()&1){
rt=res[v].back()>>1;
res[v].pop_back();
}
for(int j=0;j<res[v].size();j++){
vec[j&1].push_back(make_pair(res[v][j]>>1,res[v][j]&1));
}
res[v].clear();
}
}
for(int i=vec[0].size()-1;i>=0;i--)printf("%d ",vec[0][i].first);
if(rt)printf("%d ",rt);
for(int i=0;i<vec[1].size();i++)printf("%d ",vec[1][i].first);
puts("");
for(int i=vec[0].size()-1;i>=0;i--)printf("%d ",vec[0][i].second^1);
if(rt)printf("0 ");
for(int i=0;i<vec[1].size();i++)printf("%d ",vec[1][i].second);
puts("");
return 0;
}
欧拉回路与哈密顿回路
哈密顿图是一个无向图,在图论中是指含有哈密顿回路的图,闭合的哈密顿路径称作哈密顿回路,含有图中所有顶点的路径称作哈密顿路径。
[IOI2016]railroad
有 \(n\) 个车站,进入车站的速度不能高于 \(s_i\) ,出站后速度固定 \(t_i\) ,可以用 \(x\) 的代价使车速降低 \(x\),排列车站使得代价最小。
solution
我们考虑对于每个速度建一个点,车站……好像要连很多边,必然炸空间,不能这么搞。
我们略微转化一下题意:有 \(n\) 个车站,进入车站的速度必须恰好为 \(s_i\) ,出站后速度固定 \(t_i\) ,可以用 \(x\) 的代价使车速降低 \(x\),提速没有任何代价,排列车站使得代价最小。
这样有了一个显然的模型:先离散化,对于每个速度建一个点,每个车站从 \(s_i\) 到 \(t_i\) 连边,接下来建一个虚点 \(\infty\),\(\infty\) 到 \(1\) 连边,\(\infty-1\)(也就是离散化之后的最大值)到 \(\infty\) 连边,然后相邻两点连双向边,正向的费用为 \(0\),反向的费用为两点的速度差值。然后在这个图上跑最小哈密尔顿回路。
这是一个 \(\text{NPC}\) 问题。
我们考虑把哈密尔顿回路问题转化成欧拉回路问题。
想到可以先不连相邻两点之间的边,然后写一个算法实现只添加必须要变速的边,这样每个边都会走到,于是变成了一个图上添加权值和尽可能小的边使这个图变成欧拉回路的问题。
不难发现我们要添加相邻两点的边当且仅当覆盖了这条边的向左的边和向右的边数量不一致。而这个东西容易差分得到。如果向左的边多,那么我们添加的是若干条费用为 \(0\) 的加速边,没有贡献;如果向右的边多,我们添加若干条费用为两点速度差的边,这时计算贡献。
做完这个操作之后我们会得到若干个存在欧拉回路的联通块,这时原图还没有欧拉回路。我们还需要把联通块连起来,这个操作每次要连一条加速边一条减速边,因此每连一次代价是两点间速度差。
显然我们只会在相邻的联通块之间连边,否则一定不优,扫一遍加边,然后跑最小生成树即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int s[200005],t[200005],sum[400005];
vector<int> hsh;
int dsu[400005];
int find(int x){
return dsu[x]==x?x:dsu[x]=find(dsu[x]);
}
struct node{
int x,y,v;
node(int _x,int _y,int _v){
x=_x;y=_y;v=_v;
}
inline bool operator <(const node &b)const{
return v<b.v;
}
};
vector<node> vec;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d%d",&s[i],&t[i]);
for(int i=1;i<=n;i++)hsh.push_back(s[i]);
for(int i=1;i<=n;i++)hsh.push_back(t[i]);
sort(hsh.begin(),hsh.end());
hsh.erase(unique(hsh.begin(),hsh.end()),hsh.end());
s[++n]=hsh.back();t[n]=hsh[0];
for(int i=1;i<=n;i++)s[i]=upper_bound(hsh.begin(),hsh.end(),s[i])-hsh.begin();
for(int i=1;i<=n;i++)t[i]=upper_bound(hsh.begin(),hsh.end(),t[i])-hsh.begin();
for(int i=1;i<=hsh.size();i++)dsu[i]=i;
for(int i=1;i<=n;i++){
sum[s[i]]++;
sum[t[i]]--;dsu[find(s[i])]=find(t[i]);
}
long long ans=0;
for(int i=1;i<hsh.size();i++){
sum[i]+=sum[i-1];
if(sum[i]>0)ans+=1ll*sum[i]*(hsh[i]-hsh[i-1]);
if(sum[i]){
dsu[find(i)]=find(i+1);
}
}
for(int i=1;i<hsh.size();i++){
if(find(i)!=find(i+1)){
vec.push_back(node(find(i),find(i+1),hsh[i]-hsh[i-1]));
}
}
sort(vec.begin(),vec.end());
for(auto it:vec){
if(find(it.x)==find(it.y))continue;
ans+=it.v;
dsu[find(it.x)]=find(it.y);
}
printf("%lld\n",ans);
return 0;
}


