IOI2020国家集训队作业 Part 1
CF504E Misha and LCP on Tree
对于序列上的问题,可以考虑哈希+二分,对于树上的问题,只需使用树剖将一条路径分成序列上的 个区间即可,时间复杂度 。
CF505E Mr. Kitayuta vs. Bamboos
二分答案,考虑时光倒流,初始所有竹子高为 ,每个竹子每秒会下降 高度,你每秒可以给 个竹子拉高 ,问是否可以使得所有竹子高度在规定时间内恒 。
用堆维护每个竹子 的时间,贪心地加即可。
CF506E Mr. Kitayuta's Gift
令 表示回文串边上长为 的前后缀正好能和 、 匹配的方案数,直接以前两维为状态矩乘时是 的。
容易发现这是一个在自动机上的转移,自动机上只有两种本质不同的节点,而且经过点的顺序不影响答案,因此可以先 求出经过每种节点数的路径各有多少条,将自动机改成两条链的形式,在链之间连边,节点数是 的, 。
CF512D Fox And Travelling
一张图拓扑序前 位的数量,树形 ,背包合并即可。
CF516D Drazil and Morning Exercise
发现 以直径中点为根,向叶子方向递增,预处理之后,双指针维护即可。
CF516E Drazil and His Happy Friends
CF521D Shop
发现操作一定是先赋值,再加,再乘,加法一定是先加大的再加小的,可以预处理出前两种操作的贡献,将其统一为乘法,贪心选取即可。
CF521E Cycling City
求出一棵生成树,对于非树边,在树上打标记,分类讨论。
CF526F Pudding Monsters
转化为排列,区间合法等价于 ,即 ,由于 ,对右端点扫描线,对左端点维护区间最小值及最小值个数即可。
CF526G Spiders Evil Plan
以直径的端点做根,先不考虑 的限制,问题转化为选 个叶子使得权值和最大,显然可以贪心,然后考虑 的影响,如果当前联通块包含了 ,那么直接返回答案,否则要将原有答案去除一段,将 到它最近的被选中的祖先的一段加上,这一段有可能是那个祖先原来在的那一段,也有可能是被选中的第 段,两种情况取 即可。
CF527E Data Center Drama
将度数为奇数的点匹配,如果总边数为奇数,再加一个自环,跑欧拉回路,欧拉回路中每个点入度等于出度,隔位取反即可保证出入度均为偶数。
CF536D Tavas in Kansas
分别预处理出 到每个点的距离,然后离散化,每次至少取一个点,预处理出每个状态下一步至少要走到哪里,转移时用可以选的权值总和减去这个位置开始另一个人先手收益的后缀 即可。
CF538G Berserk Robot
将坐标系旋转 ,同时放大到原来的 倍。
这样 ULDR 对应的就是 ,可以分开考虑横纵坐标了。
另一个周期内 轴的移动距离为 ,对于 ,有 。
将坐标按 排序,对于相邻两项,有 ,这些限制可以转化为对 的限制,求解出 的范围后,选取一个合法解即可解除每个 ,进而构造出操作序列, 轴同理。
CF538H Summer Dichotomy
先不考虑 的限制,可以证明 , 是最优的。
证明如下:
将所有 当作一条数轴上的线段,那么有三种情况:
-
有三条线段两两不交,则无解。
-
所有线段两两有交,即有 ,则在这种情况下,每个老师都可以随意的选择小组。
-
,在这种情况下,显然 不能更大,而更小则不优, 同理。
因此 , 一定是最优的。
如果考虑 的限制呢?可以发现,若 ,则无论哪种情况下,只增大 是最优的;若 ,则无论哪种情况下,只减小 的最优的。
因此我们可以直接求出最优的 ,最后做一次二分图染色即可,时间复杂度 。
CF547D Mike and Fish
将横坐标或纵坐标相同的点两两匹配,剩下的则不管,考虑每个点最多连出来两条边,并且一定一条横着一条竖着,图中一定不存在奇环,对这张图二分图染色即可。
CF547E Mike and Friends
建 自动机,相当于询问 树上 有多少个节点在 末尾节点的子树中出现,扫描线即可。
CF549E Sasha Circle
CF553E Kyoya and Train
首先给出暴力 的形式:
设 表示到点 且已经过去 时间后,在最优决策下的最小花费,则我们的目标即为 。
转移如下:
其中 表示 的最小花费。
考虑这个 的正确性,由于转移时 严格变小,因此这个 实际上是个 。
直接做的话,总转移数是 的,每次转移需要 ,总时间复杂度 ,显然不够优秀。
注意到 是一个卷积,考虑分治 优化,时间复杂度降为 。
另外,在算 的时候可以 ,时间复杂度 。
CF555E Case of Computer Network
对于一个边双连通分量内部的点,我们一定有办法让它们之间可以互达,边双缩点变成一棵树,要求的就是给边定向后是否会发生冲突,树上差分打标记, 一遍即可。
CF559E Gerald and Path
首先对一端位置排序。
考虑 ,设 表示考虑前 条线段,最靠右的线段是第 条,其方向为 ( 左 右)。
考虑如何转移,从小到大枚举 后面的线段以及它的方向,同时维护枚举过的线段中最靠右的线段以及它的方向。
设线段 在 方向的右端点是 ;此时枚举到线段 ,它的方向为 ,长度为 ,右端点是 ;枚举过的线段中最靠右的线段是 ,它的方向为 ,右端点是 。
那么有转移 ,时间复杂度 。
CF566C Logistical Questions
点分治,枚举分治中心为中心算答案,对代价求导判断真正的重心在哪棵子树中。
CF566E Restoring Map
首先考虑非叶子节点,两个节点 之间有边当且仅当能找到两个集合交集恰好是 ,可以以 的复杂度将这一部分求出来,考虑给叶子节点找父亲,首先,包含这个节点的最小集合一定就是它的集合,将这个集合中的叶子节点删去就是它父亲节点与非叶子节点之间的边集,通过边集找到它的父亲,这部分的复杂度是 ,总复杂度 。
CF568C New Language
贪心枚举 , 。
CF568E Longest Increasing Subsequence
首先重复填数对答案没有影响,,所以先忽略这个条件。
记 为以 为结尾的 的长度, 为以 为结尾的 的上一位。
记 为当前长度为 的 的最小的结尾 当前长度为 的 的最小的结尾的位置。
这些都可以简单 出来。
然后我们考虑怎么构造方案。
不是 的位置 我们可以直接跳到 。
如果 所在的位置是 ,那么我们优先找 ,且 ,那么我们就跳到位置 。
否则,我们就只能跳到最近的一个 的位置,时间复杂度 。
CF571D Campus
动态开点线段树维护每个集合被修改的时间,启发式合并,同时记录每次合并的时间,只统计有用操作。
CF571E Geometric Progressions
CF573E Bear and Bowling
一个比较显然的 思路:我们设 表示前 个数已经选了 个数的最大答案,容易推出转移方程:
但是我们发现这个 是 的,考虑优化。
我们考虑 式子里面的两个元素 和 。
关键来了,我们可以发现这两个各为一个凸函数(如果把他们在 上的取值描成点连起来的话),并且这两个图像有且仅有一个交点,因为右式相当于在左式的基础上向右平移并增加一个变化的率(有点类似于加速度)。
形象来说,这两个的图像大致是这样的:
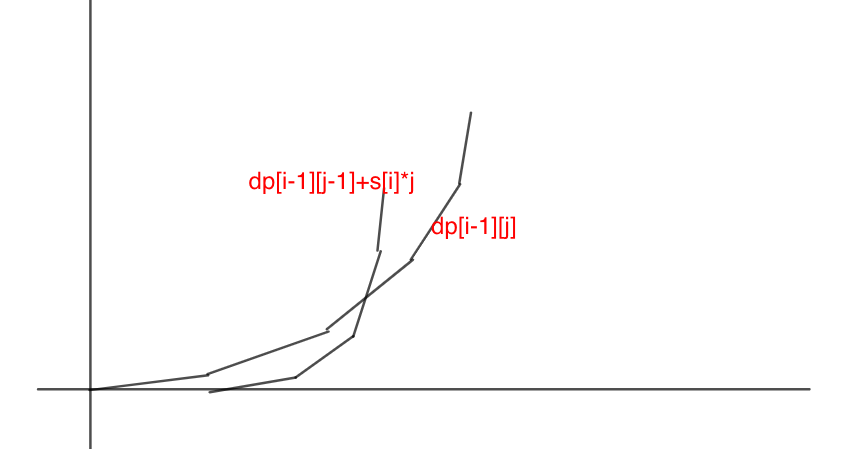
于是我们可以来二分这个具有可二分性的交点。在这个交点之前,我们取 。之后,我们取 。
然后由于式子的转移实际上是给当前的区间加上了一个等差序列,所以就可以用平衡树来维护了。
CF575A Fibonotci
容易想到矩乘,需要快速维护和计算一些矩阵的乘积,线段树即可。
CF575E Spectator Riots
CF575I Robots protection
考虑到四种方向是对称的,我们只考虑其中一种情况,比如说直角顶点在左下角的情况,令三个顶点为 。
首先我们发现需要加的所有点 ,都满足 ,这个东西用一棵树状数组就可以维护:
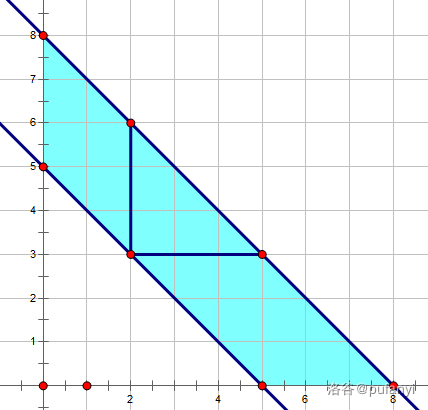
然后我们就是要减去这两块:
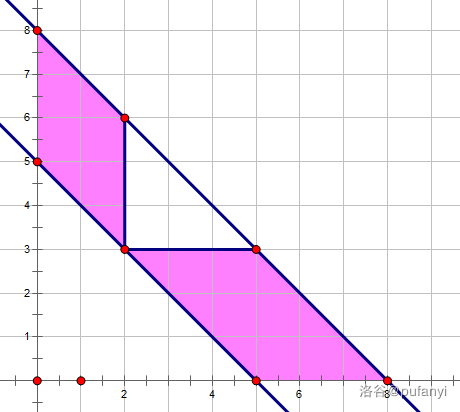
我们考虑如何减去,观察这些点的性质,首先均满足 ,然后其还满足 或 。于是我们可以考虑开两棵二维树状数组,一棵维护下标 ,另一棵维护下标 ,然后在这两棵树状数组上矩阵加即可。
时间复杂度 ,空间 。
CF576D Flights for Regular Customers
将边按时间排序,一条一条加进去, + 矩阵快速幂即可。
CF576E Painting Edges
需要开 个并查集的线段树分治判断二分图。
CF578E Walking!
显然本题等价于将字符串划分成若干个 L,R 交错的子序列, 最小化子序列的个数。
那么我们从左向右扫描字符串,贪心地将当前地字母插入之前地子序列中。
我们看看这种情况:RLLR ,这个字符串可能被我们划分成: RL 和 LR 。我们发现他没有办法拼接了,需要划分成 RLR(1,2,4) 和 L(3) 才满足条件。
分类讨论稍微有些麻烦,我们进一步观察发现我们发现我们可以将所有 RL (指开头为 R 结尾为 L 的子序列) 拼成个 RL ,LR 也可以。
所以我们发现只有当所有的子序列都为 RL 和 LR (即无 RR 和 LL )的情况我们才无法拼接,并且此时两种子序列均至少有一个。
这是我们不妨取出一个 RL 和一个 LR ,根据它们结尾的位置关系我们必然可以把它们变一个 RR 和 LL ,比如若 LR 的结尾在 RL 结尾之后,我们将 LR 的结尾接给 RL 就行了。
这样可以避免分类讨论了,时间复杂度 。
CF578F Mirror Box
我们依次考虑两个条件:
-
光线要从邻边射出:说明我们需要将每两个边缘用线封闭起来,这说明图需要是连通的,画图可以发现,不连通的画光线一定会跑出去的。
-
每一条网格线都存在 中的一条光线,满足这条光线经过这个网格线:说明不能存在环,如果有环的话,因为环是封闭的,光线不可能进入
将放镜子转化为在 的点阵中连边,将点阵黑白染色,可以发现,合法的方案对应于黑/白格子的生成树。
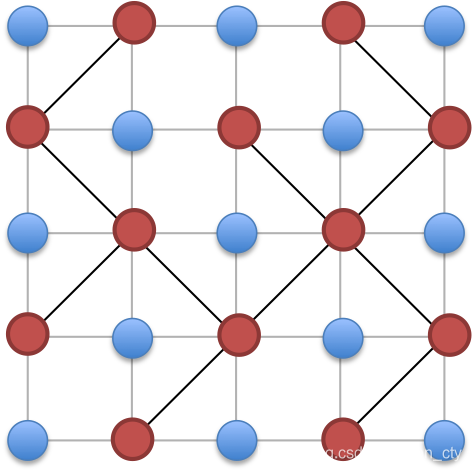
把已知的边连上并查集缩点,然后跑两遍矩阵树定理,加起来就是答案。
CF582D Number of Binominal Coefficients
令 ( 是质数, 是正整数)表示 的标准分解式中的 的幂次。
可以发现 。
将 表示为 进制数后,不难发现,在 进制下进行 和 的加法运算时,进位的次数恰好等于 。
所以将 转为 进制数(朴素实现的时间复杂度为 后进行数位 即可。
令 表示当位数从高到低考虑到 的第 位,总共进位了 次,(小于 / 等于) 且(不接受 / 接受)低一位的进位时的 的取值方案数。以 作为阶段,从大到小进行转移。则答案为 。
时间复杂度为 。
CF582E Boolean Function
先建出表达式树,设 表示树中点 处将 个值压缩成 的方案数。
对于一个非叶节点 转移为:
因此可以 优化,总时间复杂度 。
CF585E Present for Vitalik the Philatelist
令 表示最大公因数恰好为 的集合个数, 表示与 互质的数的个数。
那么我们要求的就是 。
考虑求出 和 。
考虑计算 。令 表示数 的出现次数。
莫比乌斯反演:
我们令 ; ,那么 。
发现这个 就表示 的倍数的出现次数。
再考虑求 。我们令 表示最大公因数为 的倍数的方案数。要使最大公因数为 的倍数,那么每个选的数必须是 的倍数。所以容易得到 。
我们有 。
观察上面的式子的形式,他们都是这样的形式:
其中,上面的式子为狄利克雷前缀和,下面的式子为狄利克雷后缀和。
计算 和 都是标准的狄利克雷前/后缀和形式,可以在 的时间复杂度内完成。
但还有个问题,已知 求 能做了,但是那个 的计算,是已知 求 的。
前面是加,那现在就把它逆回去就好了。具体就是把两重循环的反向,然后把加法改成减法就可以辣。当然也可以用高维前缀和的知识解释。
总时间复杂度 。
CF585F Digits of Number Pi
CF587D Duff in Mafia
首先二分答案,若此时二分的值为 ,则所有 的边都不能选。
每条边有选和不选两种状态,所以考虑 。设第 条边的状态为 表示选择它, 表示不选。连边如下:
-
对于一定不能选的边,连边 。
-
对于选出的边一定要是一个匹配,考虑一个点 上的所有边 ,连边 。
-
对于剩下的边每种颜色也一定要是一个匹配,考虑一个点 上颜色相同的所有边 ,连边 。
对于 类批量连边的情况,可以使用前缀和优化建图,时间复杂度 。
CF587F Duff is Mad
CF590E Birthday
建出 自动机,考虑建出字符串之间的包含关系图。
因为 ,所以我们不能在 自动机上暴力跳,而是在 自动机上用并查集维护 树上的上一个点,然后暴力跳 树上的父亲直到跳到一个存在的字符串即可。
然后 把多余的边建出来,直接求最长反链方案即可。
最长反链方案怎么求?
建出拆点二分图并求出其最大匹配。
考虑求出拆点二分图的最大独立集,具体操作是:
从每个没有匹配的左部点开始 ,左->右的边只走没有匹配的边,右->左的边只走匹配的边,然后所有 到的左部点和未 到的右部点就组成了最大独立集。
然后,左右都在最大独立集里的点 就在最长反链里,时间复杂度 。
CF594E Cutting the Line
CF603E Pastoral Oddities
CF605E Intergalaxy Trips
我们可以考虑倒着做,类似 的思路,每次找到当前走到 期望天数最小的,并用它更新所有点的期望天数和路径概率,直到走到 为止,时间复杂度 。
CF607E Cross Sum
CF611G New Year and Cake
CF611H New Year and Forgotten Tree
将点按照编号长度分类,一棵树合法当且仅当所有集合内的边数小于等于点数减一,这个判定速度是比较快的,每次加边时可以暴力判加入这条边后局面是否仍合法。
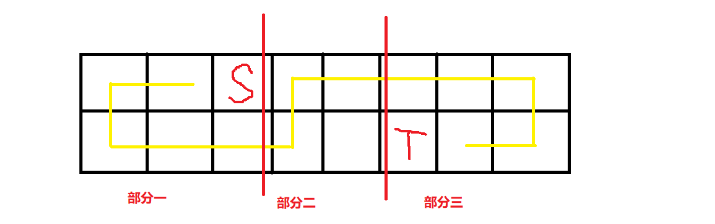
CF613E Puzzle Lover
将路径拆成三个部分,两边哈希,中间 ,需要特判长度为 和 的部分。
CF626G Raffles
CF627F Island Puzzle
树的方案是唯一的,直接把 移动到目的地判断是否合法。
环套树的情况,以 的目标为根。由于操作显然可逆,我们可以在移动 到目标后的图上讨论是否有解。
考虑 走到环上转圈的影响:把进入点先拿出来,其他点转若干圈,然后把点放回圆处。
所以所有不合法的位置只有两种情况,并且我们知道增加的边连接了哪两个点:
一条链,增加的边连接深度最深的点和深度最浅的点的父亲节点。
以同一个点为父亲的两条链,增加的边连接两条链深度最深的点。
如果不是上述两种情况或者环上除了被拿出来的点其余点通过旋转无法到达目标状态就无解,否则有解。
判断步数很简单,首先判断环是否在 到根的路径上,如果不是就先走到环上,否则就顺路把环给走完,时间复杂度 。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架