lxl 数据结构杂题选讲
CF793F Julia the snail
考虑扫描线,对于一个 \(l_i,r_i\) ,我们需要的操作就是对左端点在 \([1,l_i]\) 中且大于 \(l_i\) 的答案改为 \(r_i\) ,考虑吉司机线段树的思路,如果区间内只有最大值超过了 \(l_i\) 则暴力修改,否则递归下去,均摊复杂度 \(O(n\log n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,q;
struct node{
int mx1,mx2,lazy;bool le,ri;
node(int _mx1=0,int _mx2=0,bool _le=0,bool _ri=0){
mx1=_mx1;mx2=_mx2;le=_le;ri=_ri;lazy=0;
}
inline node operator +(node b){
node res;
if(mx1>b.mx1)return node(mx1,max(mx2,b.mx1),1,0);
if(mx1<b.mx1)return node(b.mx1,max(b.mx2,mx1),0,1);
return node(mx1,max(mx2,b.mx2),1,1);
}
}tree[400005];
void build(int l=1,int r=n,int i=1){
if(l==r){
tree[i]=node(l,0,0,0);
return ;
}
int mid=(l+r)>>1;
build(l,mid,i<<1);build(mid+1,r,i<<1|1);
tree[i]=tree[i<<1]+tree[i<<1|1];
}
inline void push(int i){
if(tree[i].le)tree[i<<1].mx1=tree[i<<1].lazy=tree[i].lazy;
if(tree[i].ri)tree[i<<1|1].mx1=tree[i<<1|1].lazy=tree[i].lazy;
tree[i].lazy=0;
}
void update(int fr,int to,int lim,int v,int l=1,int r=n,int i=1){
if(fr>r||to<l||tree[i].mx1<lim)return ;
if(fr<=l&&to>=r&&tree[i].mx2<lim){
tree[i].mx1=tree[i].lazy=v;
return ;
}
if(tree[i].lazy)push(i);
int mid=(l+r)>>1;
update(fr,to,lim,v,l,mid,i<<1);update(fr,to,lim,v,mid+1,r,i<<1|1);
tree[i]=tree[i<<1]+tree[i<<1|1];
}
int query(int loc,int l=1,int r=n,int i=1){
if(loc<l||loc>r)return 0;
if(l==r)return tree[i].mx1;
if(tree[i].lazy)push(i);
int mid=(l+r)>>1;
return query(loc,l,mid,i<<1)+query(loc,mid+1,r,i<<1|1);
}
vector<int> vec[100005];
vector<pair<int,int> > qry[100005];
int ans[100005];
int main(){
scanf("%d",&n);
scanf("%d",&m);
for(int i=1;i<=m;i++){
int l,r;scanf("%d%d",&l,&r);
vec[r].push_back(l);
}
scanf("%d",&q);
for(int i=1;i<=q;i++){
int l,r;scanf("%d%d",&l,&r);
qry[r].push_back(make_pair(l,i));
}
build();
for(int i=1;i<=n;i++){
for(auto it:vec[i])update(1,it,it,i);
for(auto it:qry[i]){
ans[it.second]=query(it.first);
}
}
for(int i=1;i<=q;i++)printf("%d\n",ans[i]);
return 0;
}
CF1446D2 Frequency Problem (Hard Version)
可以证明,这两个出现次数最多的元素中,必定有一个是全局的众数。
考虑答案一定是全局删掉一个前缀和一个后缀。
删除的过程中,全局的众数一定一直为众数,直到出现了一个与其出现次数相等的数。
假设众数 \(x\) 出现次数为 \(a\),我们目前考虑一个值 \(y\),计算 \(y\) 与 \(x\) 的答案最大是多少,\(y\) 出现 \(b\) 次。
我们如果得到一个 \(O(a+b)\) 的算法,这个题就是根号题了。
我们要得到一个 \(O(b\times \text{polylog}(n))\) 的算法。
初始将每个 \(x\) 出现的位置标记为无意义的位置。
我们枚举 \(y\) 出现的每个位置,然后找离这些位置最近的 \(x\) 出现的无意义位置(左右两边都找),然后将这些位置标记为有意义的位置。
可以证明标记结束后无意义的位置和答案无关,于是无意义的位置将序列分为多段不相关的区间。
所有有意义的位置,与 \(y\) 出现的位置,这些位置左右 \(1\) 的位置可能是答案端点,所以只有 \(O(b)\) 个可能的答案端点。
考虑为了找出答案端点,我们需要一个数据结构,支持查询前驱与删点。
这个可以使用序列线性并查集来做,对每个 \(y\) 的每个位置,预处理出其前面第一个 \(x\) 出现位置挂上去。
本题还需要支持修改后回退,由于每次修改 \(Ω(\log n)\) 次后才有可能进行一次并查集上的合并,所以复杂度正确。
将 \(x\) 的位置设为 \(1\),\(y\) 的位置设为 \(-1\),对有意义的位置跑一个前缀和,维护出和为 \(1,2,…b\) 的最长与最短前缀,这样就可以找出和为 \(0\) 的最长子段,即答案了。
如果区间中出现次数最多的数不是 \(x,y\) 也没关系,因为答案是取 \(\max\) 的,这样只是这个区间中 \(x,y\) 的贡献不够优。
所有数的出现次数和为 \(n\),故每次的 \(b\) 和是 \(O(n)\) 的,总时间复杂度 \(O(n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,s=500;
int a[200005],tot[200005],pre[400005];
int ans;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)tot[a[i]]++;
int Tmp=0;
for(int i=1;i<=n;i++)if(tot[i]>tot[Tmp])Tmp=i;
for(int t=1;t<=n;t++){
if(tot[t]<=s||tot[t]==Tmp)continue;
for(int i=0;i<=2*n;i++)pre[i]=0;
int cnt=0;
for(int i=1;i<=n;i++){
if(a[i]==Tmp)cnt++;
else if(a[i]==t)cnt--;
if(pre[cnt+n]||!cnt)ans=max(ans,i-pre[n+cnt]);
else pre[cnt+n]=i;
}
}
for(int t=1;t<=s;t++){
int cnt=0,L=0;
for(int i=1;i<=n;i++)tot[i]=0;
for(int i=1;i<=n;i++){
tot[a[i]]++;
if(tot[a[i]]==t)cnt++;
while(tot[a[i]]>t){
if(tot[a[L+1]]==t)cnt--;
tot[a[++L]]--;
}
if(cnt>=2)ans=max(ans,i-L);
}
}
printf("%d\n",ans);
return 0;
}
CF1340F Nastya and CBS
本来想用矩阵随机化,但互逆矩阵是满足交换律的,处理不了 )( 的情况。
考虑哈希,对于一个区间,消掉可以匹配的括号,剩下的如果是 ...{]... 的形式,那么剩下的部分一定不合法,因此一个可能合法的区间一定存在一个分界点,使得左边只剩右括号,右边只剩左括号。
用结构体维护一个可加可减的哈希,线段树上每个节点维护它左右两边剩余的部分,合并时要将左儿子的左括号和右儿子的右括号相抵消,对于长的那一侧像《楼房重建》那样递归下去查询即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
namespace Hashing{
const int md=1e9+7;
inline int pwr(int x,int y){
int res=1;
while(y){
if(y&1)res=1ll*res*x%md;
x=1ll*x*x%md;y>>=1;
}
return res;
}
const int B=114514,iB=pwr(B,md-2);
int _w[200015],*w=_w+100005;
inline void Init(int N){
w[0]=1;
for(int i=1;i<=N;i++){
w[i]=1ll*w[i-1]*B%md;
w[-i]=1ll*w[-i+1]*iB%md;
}
}
struct str{
int x,m;
str(){x=m=0;}
str(int v){x=v,m=1;}
str(int _x,int _m){x=_x;m=_m;}
inline bool operator ==(str b){
return m==b.m&&x==b.x;
}
inline str operator +(str b){
return str((x+1ll*b.x*w[m])%md,m+b.m);
}
inline str operator -(str b){
return str(1ll*(x-b.x+md)*w[-b.m]%md,m-b.m);
}
};
}
using Hashing::str;
int n,k,q;
struct dat{
bool err;
str vl,vr;
dat(){err=0;}
dat(int x){err=0;x>0?vr=str(x):vl=str(-x);}
}tr[400005];
str GetL(int i,int k){
if(!k)return str();
if(k==tr[i].vl.m)return tr[i].vl;
if(k<=tr[i<<1].vl.m)return GetL(i<<1,k);
return tr[i<<1].vl+(GetL(i<<1|1,k-tr[i<<1].vl.m+tr[i<<1].vr.m)-tr[i<<1].vr);
}
str GetR(int i,int k){
if(!k)return str();
if(k==tr[i].vr.m)return tr[i].vr;
if(k<=tr[i<<1|1].vr.m)return GetR(i<<1|1,k);
return tr[i<<1|1].vr+(GetR(i<<1,k-tr[i<<1|1].vr.m+tr[i<<1|1].vl.m)-tr[i<<1|1].vl);
}
inline void pushup(int i){
if(tr[i<<1].err||tr[i<<1|1].err){
tr[i].err=1;
return ;
}
tr[i].err=0;
tr[i].vl=tr[i<<1].vl;tr[i].vr=tr[i<<1|1].vr;
if(tr[i<<1].vr.m<=tr[i<<1|1].vl.m){
if(tr[i<<1].vr==GetL(i<<1|1,tr[i<<1].vr.m))tr[i].vl=tr[i].vl+(tr[i<<1|1].vl-tr[i<<1].vr);
else tr[i].err=1;
}
else{
if(tr[i<<1|1].vl==GetR(i<<1,tr[i<<1|1].vl.m))tr[i].vr=tr[i].vr+(tr[i<<1].vr-tr[i<<1|1].vl);
else tr[i].err=1;
}
}
void build(int l=1,int r=n,int i=1){
if(l==r){
int x;scanf("%d",&x);
tr[i]=x;
return ;
}
int mid=(l+r)>>1;
build(l,mid,i<<1);build(mid+1,r,i<<1|1);
pushup(i);
}
void update(int loc,int v,int l=1,int r=n,int i=1){
if(loc<l||loc>r)return ;
if(l==r){
tr[i]=v;return ;
}
int mid=(l+r)>>1;
update(loc,v,l,mid,i<<1);update(loc,v,mid+1,r,i<<1|1);
pushup(i);
}
int stk[45], tp;
void Extract(int fr,int to,int l=1,int r=n,int i=1){
if(fr>r||to<l)return ;
if(fr<=l&&to>=r){
stk[++tp]=i;return ;
}
int mid=(l+r)>>1;
Extract(fr,to,l,mid,i<<1);Extract(fr,to,mid+1,r,i<<1|1);
}
str seq[45];
str gVal(int i,int k){
if(!k)return str();
if(k==seq[i].m)return seq[i];
if(k<=tr[stk[i]].vr.m)return GetR(stk[i],k);
return tr[stk[i]].vr+(gVal(i-1,k-tr[stk[i]].vr.m+tr[stk[i]].vl.m)-tr[stk[i]].vl);
}
inline bool query(int l,int r){
tp=0;Extract(l,r);
for(int i=1;i<=tp;i++){
if(tr[stk[i]].err)return 0;
if(seq[i-1].m<tr[stk[i]].vl.m)return 0;
if(tr[stk[i]].vl==gVal(i-1,tr[stk[i]].vl.m))seq[i]=tr[stk[i]].vr+(seq[i-1]-tr[stk[i]].vl);
else return 0;
}
return !seq[tp].m;
}
int main(){
scanf("%d%d",&n,&k);
Hashing::Init(n);
build();
scanf("%d",&q);
while(q--){
int op,x,y;scanf("%d%d%d",&op,&x,&y);
if(op==1)update(x,y);
else puts(query(x,y)?"Yes":"No");
}
return 0;
}
P7290 「EZEC-5」暴力出奇迹
考虑一条竖线段 \((i,a)\) — \((i,b)\) 的贡献,它会对所有 \(x\le i\le y\),\(a\le j\le b\) 的横线段 \((x,j)\) — \((y,j)\) 加 \(1\) 。
考虑扫描线,沿着 \(x\) 轴扫描,\(\text{KDT}\) 维护,竖线段 \((i,a)\) — \((i,b)\) 相当于平面矩形加,对于询问的 \(x,y,l,r\) ,在 \(l\) 处将询问 \((x,y)\) 插入 \(\text{KDT}\) 中,在 \(r\) 处删除,并查询这个点从插入到删除过程中的历史最大值。
时间复杂度 \(O(n\sqrt m+m\log m)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,key;
vector<pair<int,int> > vec[2000005];
struct node{
int x[2],lx,rx,ly,ry,id;
node(int _x=0,int _y=0,int _id=0){
x[0]=lx=rx=_x;x[1]=ly=ry=_y;id=_id;
}
inline bool operator <(const node &b)const{
return x[key]<b.x[key];
}
}a[2000005],tree[2000005];
int le[2000005],ri[2000005],cnt,fa[2000005],mp[2000005];
int build(int l=1,int r=m,int _=0,int fi=0){
if(l>r)return 0;
int mid=(l+r)>>1,i=++cnt;key=_;fa[i]=fi;
nth_element(a+l,a+mid,a+r+1);tree[i]=a[mid];mp[a[mid].id]=i;
le[i]=build(l,mid-1,_^1,i);ri[i]=build(mid+1,r,_^1,i);
if(le[i]){
tree[i].lx=min(tree[i].lx,tree[le[i]].lx);tree[i].ly=min(tree[i].ly,tree[le[i]].ly);
tree[i].rx=max(tree[i].rx,tree[le[i]].rx);tree[i].ry=max(tree[i].ry,tree[le[i]].ry);
}
if(ri[i]){
tree[i].lx=min(tree[i].lx,tree[ri[i]].lx);tree[i].ly=min(tree[i].ly,tree[ri[i]].ly);
tree[i].rx=max(tree[i].rx,tree[ri[i]].rx);tree[i].ry=max(tree[i].ry,tree[ri[i]].ry);
}
// cout<<"build "<<" "<<tree[i].id<<" ["<<tree[i].lx<<" "<<tree[i].rx<<"] ["<<tree[i].ly<<" "<<tree[i].ry<<"]"<<endl;
return i;
}
int mx[2000005],hmx[2000005],lazy[2000005],hlazy[2000005];
inline void add(int i,int v,int hv){
hmx[i]=max(hmx[i],mx[i]+hv);hlazy[i]=max(hlazy[i],lazy[i]+hv);
mx[i]+=v;lazy[i]+=v;
}
inline void push(int i){
if(lazy[i]||hlazy[i]){
add(le[i],lazy[i],hlazy[i]);add(ri[i],lazy[i],hlazy[i]);
lazy[i]=hlazy[i]=0;
}
}
void update(int loc,int v,int i=1){
if(!i||tree[i].lx>loc||tree[i].ry<loc)return ;
if(tree[i].rx<=loc&&tree[i].ly>=loc){
// cout<<"add "<<loc<<" "<<v<<" "<<tree[i].id<<" ["<<tree[i].lx<<" "<<tree[i].rx<<"] ["<<tree[i].ly<<" "<<tree[i].ry<<"]"<<endl;
add(i,v,v);return ;
}
if(tree[i].x[0]<=loc&&tree[i].x[1]>=loc){
// cout<<"add "<<loc<<" "<<v<<" "<<tree[i].id<<" ["<<tree[i].x[0]<<"] ["<<tree[i].x[1]<<"]"<<endl;
mx[i]+=v;hmx[i]=max(hmx[i],mx[i]);
}push(i);
update(loc,v,le[i]);
update(loc,v,ri[i]);
}
int stk[2000005];
inline void insert(int id){
int top=0;
for(int i=mp[id];i;i=fa[i])stk[++top]=i;
while(top)push(stk[top--]);
int x=mp[id];hmx[x]=mx[x];
// cout<<"insert "<<id<<" "<<hmx[fa[id].back()]<<endl;
}
inline int query(int id){
int top=0;
for(int i=mp[id];i;i=fa[i])stk[++top]=i;
while(top)push(stk[top--]);
return hmx[mp[id]];
}
vector<int> Be[2000005],Ed[2000005];
int ans[2000005];
inline int read(){
int res=0;char c=getchar();
while(c<'0'||c>'9')c=getchar();
while(c>='0'&&c<='9')res=10*res+c-'0',c=getchar();
return res;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int a,b;a=read();b=read();
vec[a].push_back(make_pair(i,1));
vec[b+1].push_back(make_pair(i,-1));
}
scanf("%d",&m);
for(int i=1;i<=m;i++){
int l,r,x,y;l=read();r=read();x=read();y=read();
a[i]=node(x,y,i);
Be[l].push_back(i);
Ed[r].push_back(i);
}
build();
for(int i=1;i<=n;i++){
for(auto it:vec[i])update(it.first,it.second);
for(auto it:Be[i])insert(it);
for(auto it:Ed[i])ans[it]=query(it);
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
return 0;
}
[Ynoi2008] rdCcot
考虑对每个联通块维护一个代表元素,然后做扫描线。
每个点向深度比它小的点匹配,深度相同时编号小的点优先,容易发现这样一来每个联通块有且仅有一个元素匹配不到点,它就是我们需要的代表元素。
点分治对于每个点 \(x\) 预处理出 \(L_x=\max_{i<x,dist(i,x)\le C}\limits i\) 和 \(R_x=\min_{i>x,dist(i,x)\le C}\limits i\) ,询问 \(l,r\) 查询的就是 \(\sum_{i\in[l,r]}\limits[L_i<l]\cdot[R_i>r]\),扫描线即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,C;
int ver[600005],ne[600005],head[300005],cnt;
inline void link(int x,int y){
ver[++cnt]=y;
ne[cnt]=head[x];
head[x]=cnt;
}
int dep[300005];
void init(int x,int fi){
dep[x]=dep[fi]+1;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fi)continue;
init(u,x);
}
}
int val[300005],tree[300005],le[300005],ri[300005],rk[300005];
inline void build(){
for(int i=1;i<=n;i++)rk[i]=i;
random_shuffle(rk+1,rk+n+1);
}
inline void pushup(int x){
tree[x]=max(val[x],max(tree[le[x]],tree[ri[x]]));
}
int merge(int x,int y){
if(!x||!y)return x|y;
if(rk[x]>rk[y]){
ri[x]=merge(ri[x],y);pushup(x);
return x;
}
le[y]=merge(x,le[y]);pushup(y);
return y;
}
void split(int x,int v,int &a,int &b){
if(!x){a=0;b=0;return ;}
if(x<=v){
split(ri[x],v,ri[x],b);
a=x;
}
else {
split(le[x],v,a,le[x]);
b=x;
}pushup(x);
}
int Rt;
int Getpre(int x,int v){
if(!x)return 0;
if(ri[x]&&tree[ri[x]]>=v)return Getpre(ri[x],v);
else if(val[x]>=v)return x;
return Getpre(le[x],v);
}
int Getnxt(int x,int v){
if(!x)return n+1;
if(le[x]&&tree[le[x]]>=v)return Getnxt(le[x],v);
else if(val[x]>=v)return x;
return Getnxt(ri[x],v);
}
int siz[300005],mxp[300005],rt;
bool vis[300005];
void findrt(int x,int fi,int tot){
siz[x]=1;mxp[x]=0;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(vis[u]||u==fi)continue;
findrt(u,x,tot);siz[x]+=siz[u];
mxp[x]=max(mxp[x],siz[u]);
}
mxp[x]=max(mxp[x],tot-siz[x]);
if(mxp[x]<mxp[rt])rt=x;
}
vector<pair<int,int> > tmp;
int dis[300005];
void dfs(int x,int fi){
tmp.push_back(make_pair(dep[x],x));
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(vis[u]||u==fi)continue;
dis[u]=dis[x]+1;dfs(u,x);
}
}
int L[300005],R[300005];
void solve(int x){
vis[x]=1;tmp.clear();dis[x]=0;dfs(x,x);
sort(tmp.begin(),tmp.end());
for(auto it:tmp){
if(dis[it.second]>C)continue;
int a=0,b=0;split(Rt,it.second,a,b);
L[it.second]=max(L[it.second],Getpre(a,dis[it.second]));
R[it.second]=min(R[it.second],Getnxt(b,dis[it.second]));
tree[it.second]=val[it.second]=C-dis[it.second];le[it.second]=ri[it.second]=0;
Rt=merge(merge(a,it.second),b);
}
Rt=0;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(vis[u])continue;
mxp[rt=0]=n;findrt(u,x,siz[u]);
solve(rt);
}
}
int seg[300005];
inline void add(int x,int v){
while(x<=n+1){
seg[x]+=v;
x+=(x&-x);
}
}
inline int query(int x){
int res=0;
assert(x>=0);
while(x){
res+=seg[x];
x&=(x-1);
}
return res;
}
int ans[600005];
vector<pair<int,int> > vec[300005],qry[300005];
inline int read(){
int res=0;char c=getchar();
while(c<'0'||c>'9')c=getchar();
while(c>='0'&&c<='9')res=10*res+c-'0',c=getchar();
return res;
}
int main(){
scanf("%d%d%d",&n,&m,&C);
for(int i=2;i<=n;i++){
int x;x=read();
link(i,x);link(x,i);
}
init(1,1);
build();
for(int i=1;i<=n;i++)R[i]=n+1;
mxp[rt=0]=n;findrt(1,1,n);solve(rt);
for(int i=1;i<=m;i++){
int l,r;l=read();r=read();
qry[r].push_back(make_pair(l,i));
qry[l-1].push_back(make_pair(l,-i));
}
for(int i=1;i<=n;i++)assert(i<R[i]);
for(int i=1;i<=n;i++){
vec[i].push_back(make_pair(L[i]+1,1));
vec[i].push_back(make_pair(i+1,-1));
vec[R[i]].push_back(make_pair(L[i]+1,-1));
vec[R[i]].push_back(make_pair(i+1,1));
}
for(int i=1;i<=n;i++){
for(auto it:vec[i])add(it.first,it.second);
for(auto it:qry[i]){
ans[it.second]+=query(it.first);
}
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
return 0;
}
P6072 『MdOI R1』Path
我们以 \(1\) 为根,定义 \(a_x\) 为从 \(x\) 到 \(1\) 边权的异或值,\(in_x\) 和 \(out_x\) 为 \(x\) 子树内部和外部选择 \(u\) 和 \(v\) 中 \(a_u\oplus a_v\) 的最大值,那么最后答案显然为 \(\max_{x\ne1}\{in_x+out_x\}\) 。
对于求 \(in_x\) 我们有很多做法,例如启发式合并,\(\text{dsu on tree}\),或者可持久化 \(\text{trie}\),需要 \(O(n\log n\log\max w)\) 的时间。
对于求 \(out_x\) ,我们不妨先找到任意两个点 \(p\) 和 \(q\),使得 \(a_p\oplus a_q\) 最大,这时不以这个点对为最大值的只有 \(p\) 到根上的所有点,和 \(q\) 到根上的所有点。考虑我们只求树上一条链 \(out_x\) ,加入我们按照顺序遍历 到 \(x\),只需要将 \(x\) 父亲的子树内除去 \(x\) 子树部分加入 \(\text{trie}\) 即可。这一部分复杂度 \(O(n\log \max w)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,i,j,k,tot,totq,p=1,trie_tot=1,SZ,Ans;
int dfn[60005],siz[60005],bel[60005],dis[60005];
int fir[60005],we[120005],to[120005],nxt[120005];
int ch[1800005][2],tag[1800005],ans[60005];
struct ques {
int l,r,id;
ques(){ l=r=id=0;}
ques(int _l,int _r,int i){
l=_l,r=_r,id=i;
}
inline friend bool operator<(ques a,ques b){
if(bel[a.l]==bel[b.l])return a.r<b.r;
else return bel[a.l]<bel[b.l];
}
} q[120005];
inline void link(int u,int v,int w){
static int ce=0;
to[++ce]=v,we[ce]=w,nxt[ce]=fir[u],fir[u]=ce;
}
inline void insert(int a){
int u=1;
for(int i=30;i>=0;i--){
bool v=(a>>i)&1;
if(!ch[u][v])ch[u][v]=++trie_tot;
u=ch[u][v];tag[u]++;
}
}
inline int query(int a){
int u=1,res=0;
for(int i=30;i>=0;i--){
bool v=(a>>i)&1;
if(tag[ch[u][v^1]])res|=1<<i,u=ch[u][v^1];
else u=ch[u][v];
}
return res;
}
inline void del(int a){
int u=1;
for(int i=30;i>=0;i--){
bool v=(a>>i)&1;
u=ch[u][v];
tag[u]--;
}
}
void dfs(int u,int par,int w){
siz[u]=1,dfn[u]=++tot,dis[dfn[u]]=dis[dfn[par]]^w;
for(int i=fir[u],v;i;i=nxt[i]){
if((v=to[i])!=par){
int w=we[i];
dfs(v,u,w);
siz[u]+=siz[v];
}
}
}
inline int calc(int l,int r){
int res=0;
for(int i=l;i<=r;i++)res=max(res,query(dis[i])),insert(dis[i]);
for(int i=l;i<=r;i++)del(dis[i]);
return res;
}
inline void solve(int x){
int br=min(x*SZ,n),l=br+1,r=br;
int _ans=0;
for(;bel[q[p].l]==x;p++){
int ql=q[p].l,qr=q[p].r;
if(bel[qr]==x){ans[q[p].id]+=calc(ql,qr);continue;}
while(r<qr)_ans=max(_ans,query(dis[++r])),insert(dis[r]);
int rev=_ans;
while(l>ql)_ans=max(_ans,query(dis[--l])),insert(dis[l]);
ans[q[p].id]+=_ans;
while(l<=br)del(dis[l++]);_ans=rev;
}
while(r>br)del(dis[r--]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
int u,v,w;scanf("%d%d%d",&u,&v,&w);
link(u,v,w),link(v,u,w);
}
dfs(1,0,0);
for(int i=2;i<=n;i++)q[++totq]=ques(dfn[i],dfn[i]+siz[i]-1,i),q[++totq]=ques(dfn[i]+siz[i],dfn[i]+n-1,i);
for(int i=1;i<=n;i++)dis[i+n]=dis[i];
n<<=1;SZ=sqrt(n);
for(int i=1;i<=n;i++)bel[i]=(i-1)/ SZ+1;
sort(q+1,q+totq+1);
for(int i=1;i<=bel[n];i++)solve(i);
for(int i=1;i<=n;i++)Ans=max(Ans,ans[i]);
printf("%d\n",Ans);
return 0;
}
[Ynoi2006] rldcot
考虑扫描线,每次加入一个点 \(x\) 时将这个点到根的路径上标记上 \(x\) ,如果有某一段之前被标过号 \(y\) 了,那么这一段的底端就是点 \(x\) 和 \(y\) 的 \(\text{lca}\) ,用 \(y\) 更新一下这个点深度最后出现的位置即可,时间复杂度 \(O(n\log^2 n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int ver[200005],ne[200005],head[100005],cnt,len[200005];
inline void link(int x,int y,int v){
ver[++cnt]=y;
ne[cnt]=head[x];
head[x]=cnt;len[cnt]=v;
}
long long dep[100005];
int fa[100005];
void dfs(int x,int fi){
fa[x]=fi;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fi)continue;
dep[u]=dep[x]+len[i];
dfs(u,x);
}
}
vector<long long> hsh;
int son[2][100005],val[100005],lazy[100005];
inline bool isroot(int x){
return son[0][fa[x]]!=x&&son[1][fa[x]]!=x;
}
inline void push(int x){
if(lazy[x]){
val[son[0][x]]=lazy[son[0][x]]=lazy[x];
val[son[1][x]]=lazy[son[1][x]]=lazy[x];
}
lazy[x]=0;
}
inline void rotate(int x){
int y=fa[x],z=fa[y];
if(!isroot(y))son[son[1][z]==y][z]=x;
bool is=(son[1][y]==x);
son[is][y]=son[!is][x];fa[son[!is][x]]=y;
son[!is][x]=y;fa[y]=x;fa[x]=z;
}
int stk[100005],top;
inline void splay(int x){
stk[++top]=x;
for(int i=x;!isroot(i);i=fa[i])stk[++top]=fa[i];
while(top)push(stk[top--]);
while(!isroot(x)){
int y=fa[x],z=fa[y];
if(!isroot(y)){
if((son[1][z]==y)^(son[1][y]==z))rotate(x);
else rotate(y);
}rotate(x);
}
}
int pre[100005],tree[100005];
inline void add(int x,int v){
while(x){
tree[x]+=v;
x&=(x-1);
}
}
inline int query(int x){
int res=0;
while(x<=n){
res+=tree[x];
x+=(x&-x);
}
return res;
}
inline void access(int x){
int tmp=x,i=0;
add(pre[dep[x]],-1);pre[dep[x]]=x;add(pre[dep[x]],1);
while(x){
splay(x);add(pre[dep[x]],-1);
pre[dep[x]]=max(pre[dep[x]],val[x]);add(pre[dep[x]],1);
son[1][x]=i;i=x;x=fa[x];
}
val[i]=lazy[i]=tmp;
}
int ans[500005];
vector<pair<int,int> > vec[100005];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
int x,y,v;scanf("%d%d%d",&x,&y,&v);
link(x,y,v);link(y,x,v);
}
dfs(1,0);
for(int i=1;i<=n;i++)hsh.push_back(dep[i]);
sort(hsh.begin(),hsh.end());hsh.erase(unique(hsh.begin(),hsh.end()),hsh.end());
for(int i=1;i<=n;i++)dep[i]=upper_bound(hsh.begin(),hsh.end(),dep[i])-hsh.begin();
for(int i=1;i<=m;i++){
int l,r;scanf("%d%d",&l,&r);
vec[r].push_back(make_pair(l,i));
}
for(int i=1;i<=n;i++){
access(i);
for(auto it:vec[i])ans[it.second]=query(it.first);
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
return 0;
}
P6071 『MdOI R1』Treequery
给定一个点 \(x\) ,询问 \(x\) 到 \([l,r]\) 内的点组成的虚树的距离,对于点 \(x\) 与虚树 \([l,r]\) 的关系分类讨论即可。
如果 \([l,r]\) 一部分在 \(x\) 子树内,一部分在子树外,答案为 \(0\) 。
如果 \([l,r]\) 全部在 \(x\) 子树内,答案为点 \(x\) 到 \([l,r]\) 的 \(\text{lca}\) 的距离。
如果 \([l,r]\) 全部在 \(x\) 子树外,答案为点 \(x\) 到其在 \([l,r]\) 内 \(\text{dfs}\) 序上的前驱和后继的之间的链的距离。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,q;
int ver[400005],ne[400005],head[400005],tot,val[400005];
inline void link(int x,int y,int v){
ver[++tot]=y;
ne[tot]=head[x];
head[x]=tot;val[tot]=v;
}
int siz[200005],son[200005],fa[200005];
long long dep[200005];
void dfs1(int x,int fi){
siz[x]=1;fa[x]=fi;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fi)continue;
dep[u]=dep[x]+val[i];
dfs1(u,x);siz[x]+=siz[u];
if(siz[u]>siz[son[x]])son[x]=u;
}
}
int dfn[200005],cnt,top[200005],mp[200005];
void dfs2(int x,int fi){
dfn[x]=++cnt;top[x]=fi;mp[cnt]=x;
if(son[x])dfs2(son[x],fi);
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fa[x]||u==son[x])continue;
dfs2(u,u);
}
}
inline int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]>=dep[top[y]])x=fa[top[x]];
else y=fa[top[y]];swap(x,y);
}return dep[x]<dep[y]?x:y;
}
inline long long dist(int x,int y){
int lc=lca(x,y);
return dep[x]+dep[y]-2*dep[lc];
}
int tree[4000005],rt[200005],le[4000005],ri[4000005];
int insert(int loc,int old,int l=1,int r=n){
if(loc<l||loc>r)return old;
int i=++cnt;tree[i]=tree[old]+1;
if(l==r)return i;
int mid=(l+r)>>1;
le[i]=insert(loc,le[old],l,mid);ri[i]=insert(loc,ri[old],mid+1,r);
return i;
}
int query(int fr,int to,int a,int b,int l=1,int r=n){
if(fr>r||to<l)return 0;
if(fr<=l&&to>=r)return tree[b]-tree[a];
int mid=(l+r)>>1;
return query(fr,to,le[a],le[b],l,mid)+query(fr,to,ri[a],ri[b],mid+1,r);
}
int find(int k,int a,int b,int l=1,int r=n){
if(l==r)return mp[l];
int mid=(l+r)>>1;
if(tree[le[b]]-tree[le[a]]>=k)return find(k,le[a],le[b],l,mid);
return find(k-tree[le[b]]+tree[le[a]],ri[a],ri[b],mid+1,r);
}
long long lstans;
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<n;i++){
int x,y,v;scanf("%d%d%d",&x,&y,&v);
link(x,y,v);link(y,x,v);
}
dfs1(1,1);dfs2(1,1);
for(int i=1;i<=n;i++)rt[i]=insert(dfn[i],rt[i-1]);
while(q--){
int x,l,r;scanf("%d%d%d",&x,&l,&r);
x^=lstans;l^=lstans;r^=lstans;
int tmp=query(dfn[x],dfn[x]+siz[x]-1,rt[l-1],rt[r]);
if(tmp==r-l+1){
int rk1=query(1,dfn[x]-1,rt[l-1],rt[r])+1,rk2=rk1+tmp-1;
rk1=find(rk1,rt[l-1],rt[r]);rk2=find(rk2,rt[l-1],rt[r]);
lstans=dist(lca(rk1,rk2),x);
}
else if(!tmp){
int rk1=query(1,dfn[x]-1,rt[l-1],rt[r]),rk2=(rk1!=r-l+1?rk1+1:0);
if(rk1)rk1=find(rk1,rt[l-1],rt[r]);if(rk2)rk2=find(rk2,rt[l-1],rt[r]);
if(rk1&&rk2)lstans=min(dep[x]-dep[lca(x,rk1)],dep[x]-dep[lca(x,rk2)]);
else {
int pre=find(1,rt[l-1],rt[r]),suf=find(r-l+1,rt[l-1],rt[r]);
if(rk1){
lstans=dist(x,lca(pre,rk1));
int t=lca(x,rk1);
if(dist(pre,rk1)==dist(pre,t)+dist(t,rk1))lstans=min(lstans,dep[x]-dep[t]);
}
else if(rk2){
lstans=dist(x,lca(suf,rk2));
int t=lca(x,rk2);
if(dist(suf,rk2)==dist(suf,t)+dist(t,rk2))lstans=min(lstans,dep[x]-dep[t]);
}
}
}
else {
lstans=0;
}
printf("%lld\n",lstans);
}
return 0;
}
[Ynoi2008] rrusq
考虑扫描线,对于每个点 \((i,p_i)\) 记录它最晚被覆盖到的时间,我们需要做的就是批量更新一个矩形内的点,并维护在每个时间点被覆盖的点的权值和。
对点建出 \(\text{KDT}\) , 每次询问在 \(\text{KDT}\) 上打标记并把子树内的所有标记收回。因为收回标记对应着打标记,所以复杂度仍然是 \(\Theta(m)\) 次遍历 \(\text{KDT}\) 的复杂度 , 即 \(\Theta(m\sqrt n)\) 次打标记/收回标记的操作。
现在我们要完成的问题变成了支持 \(\Theta(m\sqrt n)\) 次单点修改和 \(\Theta(m)\) 次后缀查询的数据结构 , 不难发现可以用 \(\Theta(1)-\Theta(\sqrt m)\) 的分块来实现它。
时间复杂度 \(\Theta(n\sqrt m+m\sqrt n)\) , 空间复杂度 \(\Theta(n+m)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,q,key;
struct node{
int x[2],v,sum;
int lx,rx,ly,ry;
node(int _x=0,int _y=0,int _v=0){
lx=rx=x[0]=_x;ly=ry=x[1]=_y;sum=v=_v;
}
inline bool operator <(const node &b)const{
return x[key]<b.x[key];
}
}a[100005],tree[100005];
int le[100005],ri[100005],cnt;
int build(int l=1,int r=n,int _=0){
if(l>r)return 0;
int i=++cnt,mid=(l+r)>>1;key=_;
nth_element(a+l,a+mid,a+r+1);tree[i]=a[mid];
le[i]=build(l,mid-1,_^1);ri[i]=build(mid+1,r,_^1);
if(le[i]){
tree[i].lx=min(tree[i].lx,tree[le[i]].lx);tree[i].ly=min(tree[i].ly,tree[le[i]].ly);
tree[i].rx=max(tree[i].rx,tree[le[i]].rx);tree[i].ry=max(tree[i].ry,tree[le[i]].ry);
tree[i].sum+=tree[le[i]].sum;
}
if(ri[i]){
tree[i].lx=min(tree[i].lx,tree[ri[i]].lx);tree[i].ly=min(tree[i].ly,tree[ri[i]].ly);
tree[i].rx=max(tree[i].rx,tree[ri[i]].rx);tree[i].ry=max(tree[i].ry,tree[ri[i]].ry);
tree[i].sum+=tree[ri[i]].sum;
}
return i;
}
int col[100005],tag[100005],lazy[100005];
inline void push(int i){
if(lazy[i]){
col[le[i]]=tag[le[i]]=lazy[le[i]]=lazy[i];
col[ri[i]]=tag[ri[i]]=lazy[ri[i]]=lazy[i];
}
lazy[i]=0;
}
inline void pushup(int i){
tag[i]=col[i];
if(le[i]&&tag[le[i]]!=tag[i])tag[i]=-1;
if(ri[i]&&tag[ri[i]]!=tag[i])tag[i]=-1;
}
namespace Block{
int s=500,sqr[100005],le[100005],ri[100005];
int a[100005],tot[505];
inline void init(){
for(int i=1;i<=m;i++)sqr[i]=i/s+1;
for(int i=1;i<=m;i++)ri[sqr[i]]=i;
for(int i=m;i>=1;i--)le[sqr[i]]=i;
}
inline void add(int x,int v){
a[x]+=v;tot[sqr[x]]+=v;
}
inline int query(int l,int r){
int res=0;
for(int i=l;i<=ri[sqr[l]]&&i<=r;i++)res+=a[i];
if(sqr[l]==sqr[r])return res;
for(int i=sqr[l]+1;i<sqr[r];i++)res+=tot[i];
for(int i=le[sqr[r]];i<=r;i++)res+=a[i];
return res;
}
}
void update(int lx,int rx,int ly,int ry,int v,int i=1){
if(!i||rx<tree[i].lx||lx>tree[i].rx||ry<tree[i].ly||ly>tree[i].ry)return ;
if(~tag[i]&&lx<=tree[i].lx&&tree[i].rx<=rx&&ly<=tree[i].ly&&tree[i].ry<=ry){
Block::add(tag[i],-tree[i].sum);
col[i]=tag[i]=lazy[i]=v;
Block::add(tag[i],tree[i].sum);return ;
}push(i);
if(lx<=tree[i].x[0]&&tree[i].x[0]<=rx&&ly<=tree[i].x[1]&&tree[i].x[1]<=ry){
Block::add(col[i],-tree[i].v);
col[i]=tag[i]=v;
Block::add(col[i],tree[i].v);
}
update(lx,rx,ly,ry,v,le[i]);
update(lx,rx,ly,ry,v,ri[i]);
pushup(i);
}
int X1[100005],X2[100005],Y1[100005],Y2[100005];
vector<pair<int,int> > vec[100005];
int ans[1000005];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x,v;scanf("%d%d",&x,&v);
a[i]=node(i,x,v);
}
build();
scanf("%d",&m);Block::init();
for(int i=1;i<=m;i++)scanf("%d%d%d%d",&X1[i],&X2[i],&Y1[i],&Y2[i]);
scanf("%d",&q);
for(int i=1;i<=q;i++){
int l,r;scanf("%d%d",&l,&r);
vec[r].push_back(make_pair(l,i));
}
for(int i=1;i<=m;i++){
update(X1[i],X2[i],Y1[i],Y2[i],i);
for(auto it:vec[i]){
ans[it.second]=Block::query(it.first,i);
}
}
for(int i=1;i<=q;i++)printf("%d\n",ans[i]);
return 0;
}
转转的数据结构题
考虑扫描线,\(\text{ODT}\) 维护序列上的连续段,树状数组维护每次操作剩余的对序列的贡献。
点击查看代码
[Ynoi2009] rprmq1
考虑扫描线,因为这个信息不具有可减性,考虑对平面进行分治,每次分治的时候,处理跨过分治中线的询问。
这样一来就把询问拆成了分治中线两侧的一个前缀和一个后缀。
然后我们只需对两边分别做扫描线,维护扫过部分的历史最大值即可,为了让分治的复杂度正确,可以和莫队类似,试着利用之前的信息。
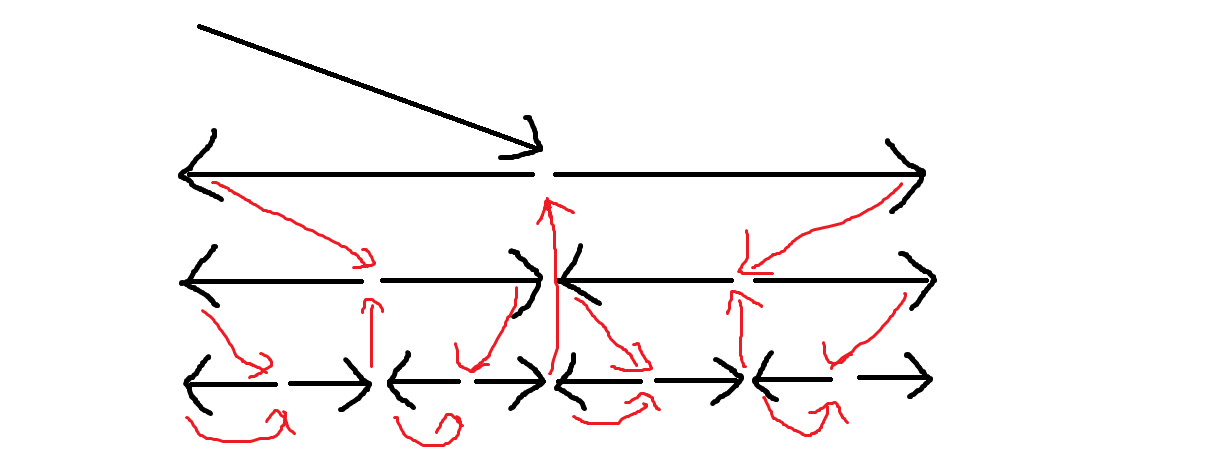
图中是分治的过程,其中红线表示撤回一些修改,并将历史最值设为当前值。后者打标记即可,不过打标记之前要将节点原有的加法标记下传.
否则如果它的加法标记为负数,这个标记将无法加到其子节点的历史最值上。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,q;
long long mx[400005],hmx[400005],lazy[400005],hlazy[400005];
bool cov[400005];
inline void add(int i,long long v,long long hv){
hlazy[i]=max(hlazy[i],lazy[i]+hv);
hmx[i]=max(hmx[i],mx[i]+hv);mx[i]+=v;lazy[i]+=v;
}
inline void reset(int i){
if(lazy[i]||hlazy[i]){
add(i<<1,lazy[i],lazy[i]);add(i<<1|1,lazy[i],lazy[i]);
lazy[i]=hlazy[i]=0;
}
hmx[i]=mx[i];hlazy[i]=lazy[i];cov[i]=1;
}
inline void push(int i){
if(cov[i]){
reset(i<<1);reset(i<<1|1);
cov[i]=0;
}
if(lazy[i]||hlazy[i]){
add(i<<1,lazy[i],hlazy[i]);add(i<<1|1,lazy[i],hlazy[i]);
lazy[i]=hlazy[i]=0;
}
}
void update(int fr,int to,long long v,int l=1,int r=n,int i=1){
if(fr>r||to<l)return ;
if(fr<=l&&to>=r){
add(i,v,v);return ;
}
int mid=(l+r)>>1;push(i);
update(fr,to,v,l,mid,i<<1);update(fr,to,v,mid+1,r,i<<1|1);
mx[i]=max(mx[i<<1],mx[i<<1|1]);
hmx[i]=max(hmx[i<<1],hmx[i<<1|1]);
}
long long query(int fr,int to,int l=1,int r=n,int i=1){
if(fr>r||to<l)return -1e18;
if(fr<=l&&to>=r)return hmx[i];
int mid=(l+r)>>1;push(i);
return max(query(fr,to,l,mid,i<<1),query(fr,to,mid+1,r,i<<1|1));
}
struct data{
int l,r,v;
data(int _l,int _r,int _v){
l=_l;r=_r;v=_v;
}
};
vector<data> L[50005],R[50005];
int le[500005],ri[500005],up[500005],down[500005];
long long ans[500005];
vector<int> qryl[50005],qryr[50005];
void solve(int l,int r,int mid){
// cout<<"solve "<<l<<" "<<r<<" "<<mid<<endl;
for(int i=mid;i>=l;i--){
for(auto it:R[i])update(it.l,it.r,it.v);
for(auto it:qryl[i]){
if(ri[it]>=mid&&ri[it]<=r)ans[it]=max(ans[it],query(down[it],up[it]));
//,cout<<"ri "<<it<<" "<<ans[it]<<endl;
}
for(auto it:L[i])update(it.l,it.r,-it.v);
}
if(l!=r){
int midl=(l+mid)>>1;
for(int i=l;i<=midl;i++){
for(auto it:R[i])update(it.l,it.r,-it.v);
for(auto it:L[i])update(it.l,it.r,it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
solve(l,mid,midl);
for(int i=midl+1;i<=mid;i++){
for(auto it:R[i])update(it.l,it.r,-it.v);
for(auto it:L[i])update(it.l,it.r,it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
}
else {
for(int i=l;i<=mid;i++){
for(auto it:R[i])update(it.l,it.r,-it.v);
for(auto it:L[i])update(it.l,it.r,it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
}
for(int i=mid+1;i<=r;i++){
for(auto it:L[i])update(it.l,it.r,it.v);
for(auto it:qryr[i]){
if(le[it]<=mid+1&&le[it]>=l)ans[it]=max(ans[it],query(down[it],up[it]));
//,cout<<"le "<<it<<" "<<ans[it]<<endl;
}
for(auto it:R[i])update(it.l,it.r,-it.v);
}
if(l!=r){
int midr=(mid+1+r)>>1;
for(int i=r;i>midr;i--){
for(auto it:L[i])update(it.l,it.r,-it.v);
for(auto it:R[i])update(it.l,it.r,it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
solve(mid+1,r,midr);
for(int i=midr;i>mid;i--){
for(auto it:L[i])update(it.l,it.r,-it.v);
for(auto it:R[i])update(it.l,it.r,it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
}
else {
for(int i=r;i>=mid+1;i--){
for(auto it:L[i])update(it.l,it.r,-it.v);
for(auto it:R[i])update(it.l,it.r,it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
}
// cout<<"solved "<<l<<" "<<r<<" "<<mid<<endl;
}
inline int read(){
int res=0;char c=getchar();
while(c<'0'||c>'9')c=getchar();
while(c>='0'&&c<='9')res=10*res+c-'0',c=getchar();
return res;
}
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++){
int l1,l2,r1,r2,v;l1=read();l2=read();r1=read();r2=read();v=read();
L[l1].push_back(data(l2,r2,v));
R[r1].push_back(data(l2,r2,v));
}
for(int i=1;i<=q;i++){
le[i]=read();down[i]=read();ri[i]=read();up[i]=read();
qryl[le[i]].push_back(i);
qryr[ri[i]].push_back(i);
}
int mid=(1+n)>>1;
for(int i=1;i<=mid;i++){
for(auto it:L[i])update(it.l,it.r,it.v);
for(auto it:R[i])update(it.l,it.r,-it.v);
}
hmx[1]=mx[1];hlazy[1]=lazy[1];cov[1]=1;
solve(1,n,mid);
for(int i=1;i<=q;i++)printf("%lld\n",ans[i]);
return 0;
}
[Ynoi2008] rupq
使用平衡树维护序列,这样可以支持分裂合并。
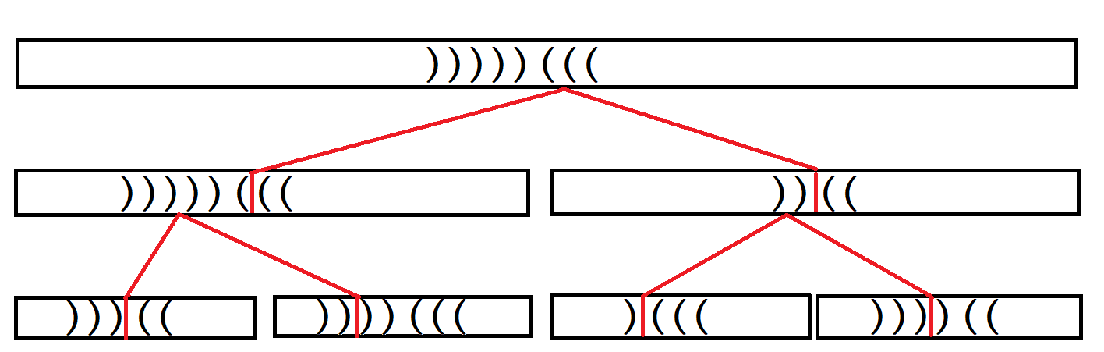
虽然 \(\text{NAND}\) 没有结合律,但是可以维护它的真值表,使得 \(\max\) 和 \(\text{NAND}\) 都可以写做半群信息的形式,所以直接 \(O(1)\) 合并即可,每个区间的括号合并完成后应该是形如 ))))(((( 的样子。
考虑怎么合并两个儿子的信息,不失一般性,设左儿子的 ( 数量多于右儿子的 ) 数量,其它的情况类似。
那么匹配完成后分为三部分,左儿子的 )))),左儿子的 ( 和右儿子的 ) 匹配之后左儿子剩下的 ((,右儿子的 ((((。
假如我们分别维护了 )))) 和 (((( 对应的信息,那么我们只需要考虑中间的部分如何维护。
计算左儿子的前若干个 ( 的信息,于是实现函数 \(\text{GetL(u,k)}\) 表示计算节点 \(u\) 的前 \(k\) 个 ( 的信息。
每次只需要向一边递归,复杂度 \(O(\log n)\),总时间复杂度 \(O(n+m\log^2n)\) 。
点击查看代码
#515. 【UR #19】前进四
容易想到一种类似于楼房重建的方式做到 \(O(n\log^2n)\) ,但是这是不够的,考虑单 \(\log\) 做法。
发现询问都为后缀,以时间为轴开线段树,倒序扫描序列,对于每个位置,每个数出现的时间都是一段区间,吉如一线段树维护每个位置被取 \(\min\) 的次数即可,时间复杂度 \(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,q;
struct data{
int x,l,r;
data(int _x,int _l,int _r){
x=_x;l=_l;r=_r;
}
};
vector<data> vec[1000005];
vector<int> qry[1000005];
struct node{
int mx1,mx2;
node(){}
node(int _mx1,int _mx2){
mx1=_mx1;mx2=_mx2;
}
inline node operator +(const node &b)const{
if(mx1>b.mx1)return node(mx1,max(mx2,b.mx1));
if(mx1<b.mx1)return node(b.mx1,max(b.mx2,mx1));
return node(mx1,max(mx2,b.mx2));
}
}tree[4000005];
int lazy[4000005];
inline void push(int i){
if(!lazy[i])return ;
if(tree[i<<1].mx1>tree[i].mx1)tree[i<<1].mx1=tree[i].mx1,lazy[i<<1]+=lazy[i];
if(tree[i<<1|1].mx1>tree[i].mx1)tree[i<<1|1].mx1=tree[i].mx1,lazy[i<<1|1]+=lazy[i];
lazy[i]=0;
}
void build(int l=0,int r=q,int i=1){
tree[i]=node(1e9,0);
if(l==r)return ;
int mid=(l+r)>>1;
build(l,mid,i<<1);build(mid+1,r,i<<1|1);
}
void update(int fr,int to,int v,int l=0,int r=q,int i=1){
if(fr>r||to<l||tree[i].mx1<=v)return ;
if(fr<=l&&to>=r&&tree[i].mx2<v){
lazy[i]++;tree[i].mx1=v;
return ;
}
int mid=(l+r)>>1;push(i);
update(fr,to,v,l,mid,i<<1);update(fr,to,v,mid+1,r,i<<1|1);
tree[i]=tree[i<<1]+tree[i<<1|1];
}
int query(int loc,int l=0,int r=q,int i=1){
if(loc<l||loc>r)return 0;
if(l==r)return lazy[i];
int mid=(l+r)>>1;push(i);
return query(loc,l,mid,i<<1)+query(loc,mid+1,r,i<<1|1);
}
int ans[1000005];
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
vec[i].push_back(data(x,0,q));
}
for(int i=1;i<=q;i++){
int op,x,y;
scanf("%d",&op);
if(op==1){
scanf("%d%d",&x,&y);
vec[x].back().r=i-1;vec[x].push_back(data(y,i,q));
}
else if(op==2){
scanf("%d",&x);qry[x].push_back(i);
}
}
build();
for(int i=n;i;i--){
for(auto it:vec[i])update(it.l,it.r,it.x);
for(auto it:qry[i])ans[it]=query(it);
}
for(int i=1;i<=q;i++)if(ans[i])printf("%d\n",ans[i]);
return 0;
}

