相似变换与相似矩阵

对于同一个向量，选取的基底不同，其所对应的坐标值就不同。

例如：

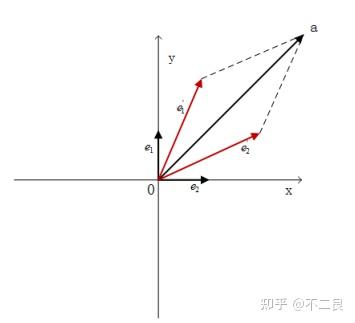
向量 \(a\) 在空间中的位置是固定的，如果使用第一组基底 \((e_1,e_2)=(\begin{bmatrix}1\\0 \end{bmatrix},\begin{bmatrix}0\\1 \end{bmatrix})\)。

向量 \(a\) 表示为 \(3\begin{bmatrix}1\\0 \end{bmatrix}+3\begin{bmatrix}0\\1 \end{bmatrix}\) ，那么在此基底下，向量 \(a\) 的坐标为 \(\begin{bmatrix}3\\3\end{bmatrix}\) 。

如果基底换为 \((e_1',e_2')=1\begin{bmatrix}2\\1 \end{bmatrix}+1\begin{bmatrix}1\\2 \end{bmatrix}\) 下，其坐标为 \(\begin{bmatrix}1\\1\end{bmatrix}\) 。

描述线性变换的矩阵也取决于基底 基底不同，描述向量线性变换的矩阵也不同 。

对于动态的向量变换，如向量从某个空间中的 位置 \(P\) 移动到 位置 \(Q\)，可以用矩阵来表示向量空间位置的改变。

如果选取的基底不同，同一个运动在不同基底下，显然对应的矩阵表示也是不同的。

例如：

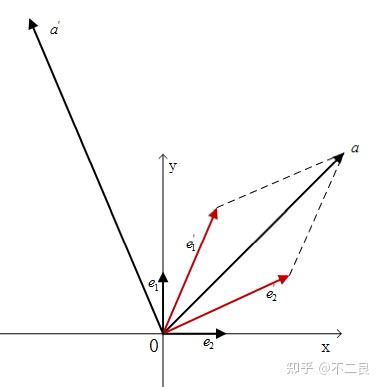
在这个二维空间中，向量从 \(a\) 变换到 \(a'\)。在基底 \((\begin{bmatrix}1\\0 \end{bmatrix},\begin{bmatrix}0\\1 \end{bmatrix})\) 的描述下，其坐标从 \(\begin{bmatrix}3\\3\end{bmatrix}\) 变换到 \(\begin{bmatrix}-3\\6\end{bmatrix}\) ，对应于这个线性变换的矩阵为 \(\begin{bmatrix}1&-2\\1 &1\end{bmatrix}\) 。

但是如果是在基底 \((\begin{bmatrix}2\\1 \end{bmatrix},\begin{bmatrix}1\\2 \end{bmatrix})\) 的描述下，其坐标的转换变成了 \(\begin{bmatrix}1\\1\end{bmatrix}\to \begin{bmatrix}-4\\5\end{bmatrix}\) 。

显然前一个基底下的变换矩阵就无法表示这个基底下的变换了。因为 \(\begin{bmatrix}1&-2\\1 &1\end{bmatrix}\times \begin{bmatrix}1\\1\end{bmatrix}\neq \begin{bmatrix}-4\\5\end{bmatrix}\) 。

相似矩阵与相似变换

针对指定向量的 同一个空间变换，用来 在不同基底下进行描述 的 不同矩阵，彼此之间称之为相似矩阵。

相似矩阵所表示的线性变换，彼此之间称之为相似变换。

在基底 \((e_1,e_2)\) 下，坐标为 \(x\) 的向量通过矩阵 \(A\) 完成了线性变换，线性变换后的坐标为 \(x'\)。

我们也可以通过矩阵 \(P\)，将向量变换到基底 \((e_1',e_2')\) 下的坐标表示，即用新的基底下的坐标来表示向量，记作 \(Px\) 。

这时在新的基底下，用来表示上面同一个空间变换的是另一个矩阵 \(B\)，即基底 \((e_1',e_2')\) 下变换后的目标坐标为 \(BPx\)。

最终我们还是需要在原基底坐标系下讨论和比较问题，因此我们再次把坐标从基底 \((e_1',e_2')\) 变回到 \((e_1,e_2)\) 下，这显然是一个逆变换，即左乘一个逆矩阵，因此和最初直接用矩阵 \(A\) 变换殊途同归。

即：

\[P^{-1}BPx=Ax \]

\[P^{-1}BP=A \]

其中 \(A\) 和 \(B\) 就是相似矩阵，表示了向量在两个基底 \((e_1,e_2)\) 和 \((e_1',e_2')\) 下的相似变换。

相似矩阵的转换关系与各自基底的转换关系相对应

具体这个矩阵 \(P\) 该如何表示呢，或是说它是如何得到的？我们来分析一下这个过程，即：向量在空间中发生一次线性变换，由空间位置 \(M\) 变到空间位置 \(N\)。如图所示：

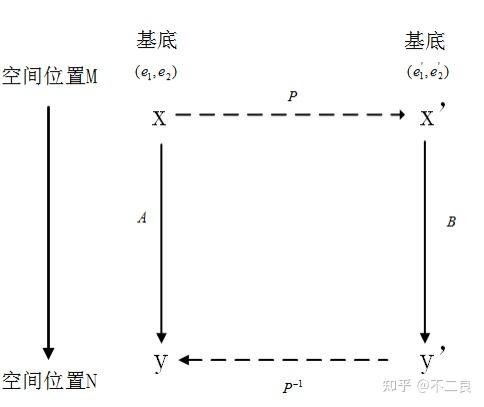
我们假设讨论的前提是：

• 在基底 \((e_1,e_2)\) 下，向量在矩阵 \(A\) 的作用下由坐标 \(x\) 变成坐标 \(y\)。

• 在基底 \((e_1',e_2')\) 下，向量在矩阵 \(B\) 的作用下由坐标 \(x'\) 变成坐标 \(y'\) ，同时 \(x'=Px\) 。

在基底 \((e_1,e_2)\) 下，向量 \(\begin{bmatrix}a\\b\end{bmatrix}\) 表示为 \(ae_1+be_2\) ，如果在基底 \((e_1',e_2')\) 下坐标该如何表示？

我们假设两组基底的线性关系如下：

\[e_1=ce_1'+de_2',\ e_2=fe_1'+ge_2' \]

明确了这层关系，我们就可以很容易的做一个基底变换：

在基底 \((e_1',e_2')\) 下，向量表示为：

\[ae_1+be_2=a(ce_1'+de_2')+b(fe_1'+ge_2') \]

其坐标为：

\[x=\begin{bmatrix}ac+bf\\ad+bg\end{bmatrix} \]

坐标可以分解成：

\[x'=\begin{bmatrix}c&f\\d&g\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix} \]

即 \(x'=\begin{bmatrix}c&f\\d&g\end{bmatrix}x\) 。那么 \(P\) 就得出来了，\(P=\begin{bmatrix}c&f\\d&g\end{bmatrix}\) ，与两组基底之间的线性关系是完全对应的。

总结：

一个向量在空间位置里，选取不同的基底，其坐标值是不同的。对于空间中同一个位置变换，在不同的基底下，用于描述的矩阵也是不同的，而这些不同矩阵所描述的线性变换是相似的，它们也称之为相似矩阵，这些矩阵之间的代数关系和其对应基底之间的数量转换关系是完全对应的。

相似矩阵的用途：矩阵的对角化

寻找相似矩阵中的最佳矩阵

这样一来，我们可以用 \(A=P^{-1}BP\) 来建立起任意两个相似 矩阵之间的代数关系，那么明确了这其中的概念之后，我们就会想这里面的用处在哪呢？

对于一个描述向量空间变换的矩阵而言，我们是否应该 选择一个最佳基底，使得我们可以用一个最佳矩阵来描述某一 个向量空间变换？

问题是：什么矩阵可以称得上是最佳矩阵？

对角矩阵的两大优势

\[A=\begin{bmatrix}a_1&&\\&a_2&\\&&a_3\end{bmatrix} \]

一方面是：一个 \(n\) 维列向量在 \(n\) 阶对角矩阵的作用下，其线性变换的方式仅仅反映在各个维度轴向上的拉伸，而不对应平移或者旋转，即：

\[Ax=\begin{bmatrix}a_1&&\\&a_2&\\&&a_3\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}a_1x_1\\a_2x_2\\a_3x_3\end{bmatrix} \]

这种线性变换所对应的操作简单、清晰。另一方面是，体现在连续的线性变换上，我们可以看出：

\[A\cdot A=\begin{bmatrix}a_1&&\\&a_2&\\&&a_3\end{bmatrix}\begin{bmatrix}a_1&&\\&a_2&\\&&a_3\end{bmatrix}=\begin{bmatrix}a_1^2&&\\&a_2^2&\\&&a_3^2\end{bmatrix} \]

因此推而广之有：

\[A^n=\begin{bmatrix}a_1&&\\&a_2&\\&&a_3\end{bmatrix}^n=\begin{bmatrix}a_1^n&&\\&a_2^n&\\&&a_3^n\end{bmatrix} \]

因此在实际使用中，可以尝试把普通的非对角矩阵转换为 与其相似的对角矩阵来进行计算处理，简化我们的过程，或者用于提取主要的特征成分等。

构造对角化转换矩阵 P 的思路

然我们知道对角矩阵是具有最佳性质的相似矩阵，并且我们可以通过 \(A=P^{-1}BP\) 得到矩阵 \(A\) 的相似对角矩阵，那么转换矩阵 \(P\) 该如何构造？

矩阵 \(P\) 和 \(A\) 一样，均为 \(n\) 阶方阵。为了方便分析和描述，我们把它写成一组列向量并排排列的形式：

\[P=\begin{bmatrix}p_1&p_2&...&p_n\end{bmatrix} \]

即 \(n\) 个 \(n\) 维列向量的横向排列。有了这个表达的基础，我们下面开始推导： 针对 \(P^{-1}AP=\Lambda\) 的表达式，两边同时左乘矩阵 \(P\)，则有 \(AP=P\Lambda\) ，我们进一步利用完整形式展开：

\[A\begin{bmatrix}p_1&p_2&...&p_n\end{bmatrix}=\begin{bmatrix}p_1&p_2&...&p_n\end{bmatrix}\begin{bmatrix}\lambda_1&&&\\&\lambda_2&&\\&&...&\\&&&\lambda_n\end{bmatrix} \]

最终有：

\[\begin{bmatrix}Ap_1&Ap_2&...&Ap_n\end{bmatrix}=\begin{bmatrix}\lambda_1p_1&\lambda_2p_2&...&\lambda_np_n\end{bmatrix} \]

看到这里，就豁然开朗了，为了上面这个等式能成立，就必须让左右两边的向量在每个维度上分别相等。即：

\[\begin{cases} Ap_1=\lambda_1p_1\\ Ap_2=\lambda_2p_2\\ \\ ...\\ Ap_n=\lambda_np_n \end{cases} \]

此时问题就进一步具体化了。 第一步是：我们要找到满足上述等式的这一组向量 \(p_1,p_2,...,p_n\) 。找到它们之后，我们将其横向排列，就构成了我们苦心寻找的转换矩阵 \(P=\begin{bmatrix}p_1&p_2&...&p_n\end{bmatrix}\) 。

引入特征向量和特征值

“特征” 二字到底指什么？

满足上文中介绍的等式：\(Ap=\lambda p\) 的非零列向量 \(p_i\) 和对应的值 \(\lambda_i\) 分别称之为方阵的特征向量和特征值。

为什么称之为“特征”？是因为这一类向量和值属于该方阵 \(A\) 的固有属性。

一般而言，对于一个向量 \(x\)，在矩阵 \(A\) 的作用下发生线性变换 \(Ax=b\)。

变换后，向量 \(x\) 的方向和长度都会发生变化，如果 \(A\) 不是方阵，连向量的维度都会发生改变。

而我们从 \(Ap=\lambda p\) 这个式子中却能够发现这个重要的现象：

在方阵 \(A\) 的变换作用下，特征向量 \(p\) 的线性变换就是在其向量方向上进行 \(\lambda\) 倍的伸缩变换。

说得更直白一些，就是仅仅只有向量的长度发生改变，但是方向并不改变，具备了这种特殊性，就称之为特征。

我们接着再观察一下对角化的等式：\(P^{-1}AP=\Lambda\) ，看看能否发现其它更多的特性。

• 首先：从等式直接看出，由特征向量构成的矩阵 \(P\) 要求是可逆的，也就是说，方阵 \(A\) 的特征向量必须满足线性无关，矩阵 \(A\) 才能进行对角化。

• 其次：我们把等式右侧移到左侧，有：\((A-\lambda I)p=0\) ，也就是说，向量 \(p\) 是矩阵 \(A-\lambda I\) 的零空间，由于向量 \(p\) 有非零的前提条件，因此 \(A-\lambda I\) 是一个不可逆矩阵。

几何意义

对于一个特定向量 \(v\)，如果我们使用默认基底 \((e_1,e_2,...,e_n)\) 对其进行表示，向量即被表示为：\(x_1e_1+x_2e_2+...+x_ne_n\) 。

使用方阵 \(A\) 对其进行线性变换，那么正如我们前面内容所介绍的，这一组默认的基底就会变成一组新的目标向量，一般情况下，原始的基向量和转换后的目标向量是不共线的。

此时，我们对该向量更换一组基底进行表示，采用方阵 \(A\) 的一组特征向量 \((p_1,p_2,...,p_n)\) 作为其新的基底。

则该向量表示为 \(y_1p_1+y_2p_2+...+y_np_n\) ，其新的坐标为 \(\begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix}\) ，在此基础上利用方阵 \(A\) 对其进行线性变换：

\[Av=A(y_1p_1+y_2p_2+...+y_np_n)=Ay_1p_1+Ay_2p_2+...+Ay_np_n \]

再用上我们前面讲过的 \(Ap=\lambda p\) ，替换一下就有：

\[Av=\lambda_1y_1p_1+\lambda_2y_2p_2+...+\lambda_ny_np_n \]

这个结果是非常漂亮的，利用基底 \((p_1,p_2,...,p_n)\) 表示的向量 \(v\)，经过矩阵 \(A\) 的线性转换，向量坐标由 \(\begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix}\) 变为 \(\begin{bmatrix}\lambda_1y_1\\\lambda_2y_2\\...\\\lambda_ny_n\end{bmatrix}\)

概括一下其几何含义：

对一个向量进行矩阵 \(A\) 描述的线性变换，如果用矩阵 \(A\) 的特征向量 \((p_1,p_2,...,p_n)\) 作为基底对该向量进行坐标表示，该空间变换即可简化为各个维度的坐标值在其基向量方向上对应伸缩 \(\lambda_i\) 倍。

任意 n 阶矩阵都可以相似成一个三角矩阵

使用归纳法。

显然，\(n=1\) 时成立，那么只需证明假设 \(n=k-1\) 成立时，有 \(n=k\) 成立，即证明该定理。

设：

\[P_1=(x_1,x_2,\cdots,x_k) \]

其中 \(x_1,x_2,\cdots,x_k\) 线性无关且 \(x_1\) 是矩阵特征值为 \(\lambda_1\) 时的特征向量（对其他向量并无要求），那么可得：

\[A_kP_1=(A_kx_1,A_kx_2,\cdots,A_kx_k)=((\lambda_1x_1,A_kx_2,\cdots,A_kx_k)) \]

以矩阵形式表示可得：

\[A_kP_1=(x_1,x_2,\cdots,x_k) \begin{bmatrix} \lambda_1&b_{12}&\cdots&b_{1k}\\ 0&b_{22}&\cdots&b_{2k}\\ \vdots&\vdots&\ddots&\vdots\\ 0&b_{k1}&\cdots&b_{kk} \end{bmatrix} \]

则：

\[P_1^{-1}A_kP_1=\begin{bmatrix} \lambda_1&b_{12}&\cdots&b_{1k}\\ 0&b_{22}&\cdots&b_{2k}\\ \vdots&\vdots&\ddots&\vdots\\ 0&b_{k1}&\cdots&b_{kk} \end{bmatrix}= \begin{bmatrix} \lambda_1&*\\ 0&A_{k-1} \end{bmatrix} \]

由假设，矩阵为 \(k-1\) 阶时结论成立，那么对于矩阵 \(A_1\) ，存在可逆矩阵 \(Q\)，使得：

\[Q^{-1}A_1Q=\begin{bmatrix} \lambda_2&*&\cdots&*\\ &\lambda_3&\ddots&\vdots\\ &&\ddots&*\\ &&&\lambda_k \end{bmatrix} \]

那么：

\[P_2=\begin{bmatrix} 1&0^T\\ 0&Q \end{bmatrix}=P_1P_2 \]

有：

\[S^{-1}AS=P_2^{-1}P_1^{-1}AP_1P_2=\begin{bmatrix} \lambda_1&*&\cdots&*\\ &\lambda_2&\ddots&\vdots\\ &&\ddots&*\\ &&&\lambda_k \end{bmatrix} \]

CF923E Perpetual Subtraction

我们设 \(f_{k,i}\) 表示 \(k\) 次过后 \(x=i\) 的概率，则有：

\[f_{k,i}=\sum\limits_{j=i}^n\frac{f_{k-1,j}}{j+1}\\ \]

令 \(F_k\) 为列向量 \(\begin{bmatrix}f_{k,0}\\\vdots\\f_{k,n}\end{bmatrix}\) ，则有：

\[\begin{bmatrix}1&\frac{1}{2}&\cdots&\frac{1}{n+1}\\0&\frac{1}{2}&\cdots&\frac{1}{n+1}\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\frac{1}{n+1}\end{bmatrix}F_k=F_{k+1} \]

设这个大方阵为 \(D\)，输入的列向量为 \(p\)。

我们要求的实际上就是 \(D^mp\)。

我们发现我们要求它的幂，考虑对角化这个矩阵。

上三角矩阵的特征值就是对角线上的所有元素，所以有：

\[G^{-1}DG=\begin{bmatrix}1&0&\cdots&0\\0&\frac{1}{2}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\frac{1}{n+1}\end{bmatrix} \]

而特征向量是可以根据定义解得：

\[(D-\lambda I)x=0 \]

把 \(\lambda=1,\cdots,\frac{1}{n+1}\) 代入，就可以解得 \(G\) 为：

\[\begin{bmatrix}(-1)^{0}{0\choose 0}&(-1)^1{1\choose 0}&\cdots&(-1)^n{n\choose 0}\\0&(-1)^2{1\choose 1}&\cdots&(-1)^{n+1}{n\choose 1}\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&(-1)^{2n}{n\choose n}\end{bmatrix} \]

一列就是一个特征向量。现在考虑求出 \(G^{-1}\) ，二项式反演可得：

\[G^{-1}=\begin{bmatrix}{0\choose 0}&{1\choose 0}&\cdots&{n\choose 0}\\0&{1\choose 1}&\cdots&{n\choose 1}\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&{n\choose n}\end{bmatrix} \]

现在问题变成给一个列向量左乘一个方阵，这个复杂度是 \(O(n^2)\) 的，不能接受，但我们的方阵比较特殊。

先考虑 \(Gp\) 的计算，设 \(q=Gp\)，则有

\[\begin{aligned} q_i=&\sum\limits_{k=i}^n(-1)^{i+k}{k\choose i}p_k\\ =&\sum\limits_{k=i}^n(-1)^{i+k}\frac{k!}{i!(k-i)!}p_k\\ =&\frac{(-1)^i}{i!}\sum\limits_{k=i}^n(-1)^{k}k!p_k\frac{1}{(k-i)!}\\ \end{aligned} \]

容易发现这是一个减法卷积可以 \(\text{NTT}\) 优化，左乘 \(G^{-1}\) 的计算和这个区别不大，就不细说了，左乘 \((G^{-1}DG)^m\) 的计算就是给每一项乘上对角线上对应的那一个数即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int md=998244353;
inline long long read(){
    long long s=0,ne=1;char c=getchar();
    for(;c<'0'||c>'9';c=getchar())if(c=='-')ne=-1;
    for(;c>='0'&&c<='9';c=getchar())s=(s<<1)+(s<<3)+c-'0';
    return s*ne;
}
inline int add(int x,int y){return x+y>=md?x+y-md:x+y;}
inline int pwr(int a,int b){
    int r=1;
    while(b){
        if(b&1)r=1ll*r*a%md;
        a=1ll*a*a%md,b>>=1;
    }
    return r;
}
inline int inv(int x){return pwr(x,md-2);}
int rev[1<<20];
inline void cg(int t[],int n){
    for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)+(i&1)*(n>>1);
    for(int i=0;i<n;i++)if(i<rev[i])swap(t[i],t[rev[i]]);
}
inline void NTT(int t[],int n,int tp){
    cg(t,n);
    for(int w=2;w<=n;w<<=1){
        int l=w>>1,gn=pwr(tp?3:inv(3),(md-1)/w);
        for(int i=0;i<n;i+=w){
            int g=1;
            for(int j=i;j<i+l;j++){
                int u=t[j],v=1ll*g*t[j+l]%md;
                t[j]=add(u,v),t[j+l]=add(u,md-v),g=1ll*g*gn%md;
            }
        }
    }
    if(!tp){
        int in=inv(n);
        for(int i=0;i<n;i++)t[i]=1ll*t[i]*in%md;
    }
}
inline void conv(int A[],int B[],int n){
    int N=1;while(N<(n<<1))N<<=1;
    NTT(A,N,1),NTT(B,N,1);
    for(int i=0;i<N;i++)A[i]=1ll*A[i]*B[i]%md;
    NTT(A,N,0);
    for(int i=n;i<N;i++)A[i]=B[i]=0;
}
int A[1<<20],B[1<<20];
int n,m,p[1<<20],fac[1<<20],ifac[1<<20],g[1<<20];
int main(){
    n=read()+1,m=read()%(md-1);
    fac[0]=1;for(int i=1;i<n;i++)fac[i]=1ll*fac[i-1]*i%md;
    ifac[n-1]=inv(fac[n-1]);for(int i=n-2;i+1;i--)ifac[i]=1ll*ifac[i+1]*(i+1)%md;
    for(int i=0;i<n;i++)p[i]=read();
    for(int i=0;i<n;i++)A[n-i-1]=1ll*fac[i]*p[i]%md;
    for(int i=0;i<n;i++)B[i]=ifac[i];
    conv(A,B,n);
    for(int i=0;i<n;i++)g[i]=1ll*ifac[i]*A[n-i-1]%md;
    for(int i=0;i<n;i++)g[i]=1ll*g[i]*inv(pwr(i+1,m))%md;
    for(int i=0;i<n;i++)A[n-i-1]=1ll*fac[i]*g[i]%md;
    for(int i=0;i<n;i++)B[i]=i&1?md-ifac[i]:ifac[i];
    conv(A,B,n);
    for(int i=0;i<n;i++)printf("%d ",int(1ll*ifac[i]*A[n-i-1]%md));puts("");
    return 0;
}