hs-black 杂题选讲
[POI2011]OKR-Periodicity
考虑递归地构造,设 \(\text{solve(s)}\) 表示字典序最小的,\(\text{border}\) 集合和 \(S\) 的 \(\text{border}\) 集合相等的字符串。
设 \(S\) 的最长 \(\text{border}\) 是 \(t\),我们分下列几种情况讨论:
第一种情况,\(S\) 不存在 \(\text{border}\),那么最优的方案就是 \(0,0...1\)(长度为 \(1\) 的话就是 \(0\))
第二种情况,\(S\) 最长 \(\text{border}\) 小于 \(⌊\dfrac{n+1}{2}⌋\),那么 \(S\) 的其他 \(\text{border}\) 也是 \(S[1,2...t]\) 的 \(\text{border}\),所以我们递归地构造 \(S[1,2...t]\),然后考虑中间段怎么填,我们先尝试全填 \(0\),如果不行就把最后一个 \(0\) 改成 \(1\),可以证明这样构造一定是合法的。
合法的条件是不出现更长的 \(\text{border}\),假设中间段填成 \(0,0...0\) 会出现更长的 \(\text{border}\),使用反证法,考虑中间段填成 \(0,0...1\) 也会出现更长的 \(\text{border}\) 。
如果新 \(\text{border}\) 的长度 \(>\dfrac{n}{2}\),这样原串的周期至少循环了两次,考虑那个先填 \(0\) 再填 \(1\) 的位置,他一定和另一个固定的位置相对应,所以 \(0/1\) 中一定有一个会破坏周期,自然也就是不存在这样的 \(\text{border}\) 。
如果新 \(\text{border}\) 的长度 \(≤\dfrac{n}{2}\),我们把新 \(\text{border}\) 的对应关系画出来:
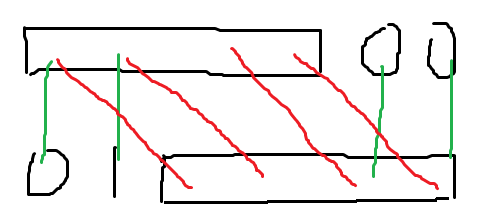
其中红线表示原来 \(\text{border}\) 的对应关系,绿线表示新 \(\text{border}\) 的对应关系。那么对于上面的最后一段 \(0\),新 \(\text{border}\) 对应到的下面的部分,一定含有一个 \(1\),导致无法匹配,所以不存在这样的 \(\text{border}\) 。
第三种情况,最短周期 \(≤⌊\dfrac{n}{2}⌋\),我们递归地构造第一个循环 \(+\) 后面的零散部分即可。
简单地说明一下正确性,设最短周期 \(p=n−t\),设某一个周期是 \(q\),我们要满足所有的 \(q\),分类讨论:
如果 \(q≤n−p\),根据弱周期引理,如果 \(p+q≤n\),那么 \(\gcd(p,q)\) 也是一个周期。由于 \(p\) 是最短周期,那么 \(q\) 一定是 \(p\) 的倍数,我们发现根据构造方法,所以 \(p\) 的倍数的周期都是能被构造出来的。
如果 \(q>n−p\),那么对应的 \(\text{border}\) 小于等于 \(p\),我们把第一个循环和后面的零散部分拼起来,一定可以表示出这样的 \(\text{border}\)(本来 \(\text{border}\) 应该使用最后一个循环,平移到第一个循环是等效的)
由于最多递归 \(O(\log n)\) 次,时间复杂度 \(O(n\log n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int T,n;
char s[200005],ans[200005];
int nxt[200005],kmp[200005];
void calc(int lim){
if(!nxt[lim]){
for(int i=1;i<lim;i++)ans[i]='0';
ans[lim]='0'+(lim!=1);
for(int i=2,j=0;i<=lim;i++){
while(j&&ans[j+1]!=ans[i])j=kmp[j];
if(ans[j+1]==ans[i])j++;
kmp[i]=j;
}
return ;
}
int to=nxt[lim];
calc(to);
for(int i=max(to+1,lim-to+1);i<=lim;i++)ans[i]=ans[i-lim+to];
if(to*2>=lim){
for(int i=to+1,j=kmp[to];i<=lim;i++){
while(j&&ans[j+1]!=ans[i])j=kmp[j];
if(ans[j+1]==ans[i])j++;
kmp[i]=j;
}
return ;
}
for(int i=to+1;i<=lim-to;i++)ans[i]='0';
for(int i=to+1,j=kmp[to];i<=lim;i++){
while(j&&ans[j+1]!=ans[i])j=kmp[j];
if(ans[j+1]==ans[i])j++;
kmp[i]=j;
}
if(kmp[lim]!=nxt[lim]){
ans[lim-to]='1';
for(int i=to+1,j=kmp[to];i<=lim;i++){
while(j&&ans[j+1]!=ans[i])j=kmp[j];
if(ans[j+1]==ans[i])j++;
kmp[i]=j;
}
}
}
inline void solve(){
scanf("%s",s+1);n=strlen(s+1);
for(int i=2,j=0;i<=n;i++){
while(j&&s[j+1]!=s[i])j=nxt[j];
if(s[j+1]==s[i])j++;
nxt[i]=j;
}
for(int i=1;i<=n;i++)kmp[i]=nxt[i];
calc(n);ans[n+1]=0;
printf("%s\n",ans+1);
}
int main(){
scanf("%d",&T);
while(T--)solve();
return 0;
}
CF1286E Fedya the Potter Strikes Back
考虑动态维护 \(\text{border}\) 集合,每次加入一个字符之后快速求出这些 \(\text{border}\) 对应的权值。
容易发现,前缀 \([1,i]\) 的所有长度大于 \(1\) 的 \(\text{border}\) 都可以从 \([1,i-1]\) 的 \(\text{border}\) 集合中继承过来。
考虑先整体继承,与 \(w[i]\) 取 \(\min\),再删去其中的不合法部分,具体步骤是:
- 如果某个原有 \(\text{border}\) 的下一位字符不是 \(s[i]\),把这个 \(\text{border}\) 删除;否则把这个位置保留。
- 如果 \(s[1]=s[i]\),那么新加入一个长度为 \(1\) 的 \(\text{border}\)。
由于最多只会有 \(O(n)\) 个 \(\text{border}\) 会被加入,所以如果我们 \(O(1)\) 地找到需要被删除的 \(\text{border}\),那么就可以暴力维护 \(\text{border}\) 集合。
不过暴力跳 \(\text{next}\) 显然是不对的,我们只需多维护一个 \(\text{anc[i]}\) 表示从 \(i\to 0\) 的这条链上第一个与 \(i\) 的后继字符不同的点,遇到不能删除的 \(\text{border}\) 时直接跳 \(\text{anc}\) 即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
const int MASK=(1<<30)-1;
char s[600005];
int w[600005],tree[2400005];
void update(int loc,int v,int l=1,int r=n,int i=1){
if(loc<l||loc>r)return ;
if(l==r){
tree[i]=v;return ;
}
int mid=(l+r)>>1;
update(loc,v,l,mid,i<<1);update(loc,v,mid+1,r,i<<1|1);
tree[i]=min(tree[i<<1],tree[i<<1|1]);
}
int query(int fr,int to,int l=1,int r=n,int i=1){
if(fr>r||to<l)return MASK;
if(fr<=l&&to>=r)return tree[i];
int mid=(l+r)>>1;
return min(query(fr,to,l,mid,i<<1),query(fr,to,mid+1,r,i<<1|1));
}
map<int,int> dp;
__int128 ans,sum;
void write(__int128 x){
if(x>=10)write(x/10);
putchar('0'+x%10);
}
int nxt[600005],anc[600005];
int main(){
scanf("%d",&n);
scanf("%s%d",&s[1],&w[1]);
ans=w[1];update(1,w[1]);
write(ans);puts("");
for(int i=2,j=0;i<=n;i++){
scanf("%s%d",&s[i],&w[i]);
s[i]=(s[i]-'a'+ans)%26+'a';w[i]^=(ans&MASK);
update(i,w[i]);
while(j&&s[j+1]!=s[i])j=nxt[j];
if(s[j+1]==s[i])j++;
nxt[i]=j;
if(s[nxt[i-1]+1]==s[i])anc[i-1]=anc[nxt[i-1]];
else anc[i-1]=nxt[i-1];
auto it=dp.upper_bound(w[i]);
int cnt=0;
while(it!=dp.end()){
sum-=1ll*it->first*it->second;
cnt+=it->second;it=dp.erase(it);
}
if(cnt)dp[w[i]]+=cnt,sum+=1ll*cnt*w[i];
for(int j=i-1;j;){
if(s[j+1]==s[i])j=anc[j];
else {
int tmp=query(i-j,i);
sum-=tmp;dp[tmp]--;
if(!dp[tmp])dp.erase(tmp);
j=nxt[j];
}
}
if(s[1]==s[i])sum+=w[i],dp[w[i]]++;
ans+=query(1,i)+sum;
write(ans);puts("");
}
return 0;
}
[JSOI2019]节日庆典
使用增量法添加字符,可以维护一个备选后缀集合,只有这个集合中的后缀才可能成为最优解,如果后缀 \(a\) 之后永远不可能成为答案,那么就把后缀 \(a\) 删除。
有一个很厉害的结论
Significant Suffixes Log Theory
称一个串 \(s\) 的 \(\text{Significant Suffixes}\) 为满足 \(∃v,t=arg\min_{u∈suffix(s)}\limits\{tv\}\) 的后缀的集合,即在拼上一个串 \(v\) 后,\(t\) 是 \(sv\) 的最小后缀。该 \(\text{Theory}\) 断言 \(s\) 的 \(\text{Significant Suffixes}\) 数量 \(≤\log |s|\) 。
证明:
对于两个属于 \(\text{Significant Suffixes}\) 的后缀 \(a,b\) ,\(|a|≥|b|\),容易由定义推出 \(b\) 是 \(a\) 的前缀,从而 \(a\) 有一个 \(|a|−|b|\) 的周期,若 \(2|b|>|a|\),则 \(a,b\) 可以分别表示 \(TTc\) 与 \(Tc\),由于存在 \(v\) 满足 \(Tcv<TTcv\),则 \(cv<Tcv\),\(cv\) 才应该是最小后缀,矛盾。从而 \(|a|≥2|b|\),所以 \(s\) 的 \(\text{Significant Suffixes}\) 数量不超过 \(\log s\) 。
可以按照证明的思路来维护这个集合,能直接区分是最好,如果区分不了可以用长度关系来判断,当小后缀的长度的两倍 \(>\) 大后缀的长度时,就可以弹出小后缀了。
在备选集合中求最优解可以考虑 \(\text{exkmp}\) 或哈希,我们求出 \(nxt[i]\) 表示后缀 \(i\) 和原串的 \(\text{lcp}\),这个问题就易于解决了,时间复杂度 \(O(n\log n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
char s[3000005];
int z[3000005];
void exkmp(){
int l=0,r=0;z[1]=n;
for(int i=2;i<=n;i++){
if(r>i)z[i]=min(z[i-l+1],r-i+1);
while(i+z[i]<=n&&s[i+z[i]]==s[z[i]+1])z[i]++;
if(i+z[i]-1>r)l=i,r=i+z[i]-1;
}
return ;
}
vector<int>now,nxt;
int main(){
scanf("%s",s+1);
n=strlen(s+1);exkmp();
for(int i=1;i<=n;i++){
now.push_back(i);
nxt.clear();
for(int j=0;j<now.size();j++){
int p=now[j];
bool flag=1;
while(!nxt.empty()){
int q=nxt.back();
if(s[i]>s[q+i-p])flag=0;
if(s[i]>=s[q+i-p])break;
nxt.pop_back();
}
if(flag&&(nxt.empty()||(i-p+1<p-nxt.back())))nxt.push_back(p);
}
now=nxt;
int pos=now[0];
for(int j=1;j<now.size();j++){
int x=now[j],k=pos+i-x;
if(z[k+1]>=i-k){
register int l=i-k;
if(z[l+1]<x-l-1&&s[l+z[l+1]+1]<s[z[l+1]+1])pos=x;
}
else if(s[z[k+1]+1]<s[k+z[k+1]+1])pos=x;
}
printf("%d ",pos);
}
return 0;
}
[ZJOI2017]字符串
此题中所求的 \(s[l..r]\) 的字典序最小的后缀显然在其 \(\text{Significant Suffixes}\) 中,于是考虑用线段树维护字符串的 \(\text{Significant Suffixes}\) 集合,每个节点就存储对应的串的集合,当 \(l=r\) 时,\(a\) 的集合即自己本身。考虑合并节点信息,对于左右两个节点对应的串 \(u,v\),因为线段树上有 \(0≤|v|−|u|≤1\),所以 \(u\) 的集合中至多有一个是在 \(uv\) 集合中的,对于 \(u\) 集合中的两个后缀 \(a,b,|a|≥|b|\),若 \(bv\) 是 \(av\) 的后缀,则根据证明应保留 \(a\),否则保留 \(av,bv\) 中字典序较小的对应的那个。
找出 \(u\) 集合中唯一可能的后缀,然后与 \(|v|\) 集合合并即可,注意这里并不需要重新检查哪些不在 \(\text{Significant Suffixes}\) 中,我们只需要保证候选集合在 \(O(\log|s|)\) 的量级便可。在查询信息时,找出 \(s[l..r]\) 在线段树上对应的区间的所有候选集合,是 \(O(\log^2n)\) 个,在其中找出最小的那个就行了。
对于判断两个串的大小关系,结合题目的修改方式容易想到用字符串哈希去维护,用线段树支持 \(O(\log n)\) 修改 \(O(\log n)\) 查询哈希值,然后二分两串 \(\text{lcp}\) 判断大小关系即可,单次 \(O(\log^2n)\) 。这样总复杂度是 \(O(n\log^3n+m\log^4n)\)。
不过注意到查询的贡献比修改多的多,考虑用分块去替代线段树,通过维护块的左侧之和与整体加标记,可以做到 \(O(\sqrt n)\) 修改 \(O(1)\) 查询。
这样总时间复杂度便为 \(O(n\log^2n+m\sqrt n+m\log^3n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,q;
namespace Hash{
const int B=500,Base=1e9+7;
int sqr[200005],le[505],ri[505];
__uint128_t hsh[200005],blo[505],tag[505],bas[505],pwr[200005];
long long a[200005],lazy[505];
inline __uint128_t Get(int x){
int id=sqr[x],y=x-le[id]+1;
return blo[id-1]*pwr[y]+tag[id]*bas[y]+hsh[x];
}
inline void init(){
for(int i=1;i<=n;i++)sqr[i]=i/B+1;
for(int i=1;i<=n;i++)ri[sqr[i]]=i;
for(int i=n;i>=1;i--)le[sqr[i]]=i;
pwr[0]=1;
for(int i=1;i<=n;i++)pwr[i]=pwr[i-1]*Base;
for(int i=1;i<=B;i++)bas[i]=bas[i-1]*Base+1;
for(int i=1;i<=n;i++)a[i]+=2e8;
for(int i=1;i<=n;i++)hsh[i]=(i==le[sqr[i]]?0:hsh[i-1])*Base+a[i];
for(int i=1;i<=sqr[n];i++)blo[i]=Get(ri[i]);
}
inline void update(int l,int r,int v){
if(sqr[l]==sqr[r]){
for(int i=l;i<=r;i++)a[i]+=v;
for(int i=l;i<=ri[sqr[l]];i++)hsh[i]=(i==le[sqr[i]]?0:hsh[i-1])*Base+a[i];
for(int i=sqr[l];i<=sqr[n];i++)blo[i]=Get(ri[i]);
return ;
}
for(int i=l;i<=ri[sqr[l]];i++)a[i]+=v;
for(int i=l;i<=ri[sqr[l]];i++)hsh[i]=(i==le[sqr[i]]?0:hsh[i-1])*Base+a[i];
blo[sqr[l]]=Get(ri[sqr[l]]);
for(int i=sqr[l]+1;i<sqr[r];i++){
lazy[i]+=v;tag[i]+=v;blo[i]=Get(ri[i]);
}
for(int i=le[sqr[r]];i<=r;i++)a[i]+=v;
for(int i=le[sqr[r]];i<=ri[sqr[r]];i++)hsh[i]=(i==le[sqr[i]]?0:hsh[i-1])*Base+a[i];
for(int i=sqr[r];i<=sqr[n];i++)blo[i]=Get(ri[i]);
}
inline long long Val(int x){
return a[x]+lazy[sqr[x]];
}
inline __uint128_t Get(int l,int r){
return (Get(r)-Get(l-1)*pwr[r-l+1]);
}
}
namespace Seg{
vector<pair<int,int> > tree[800005];
inline int cmp(pair<int,int> x,pair<int,int> y){
int lenx=x.second-x.first+1,leny=y.second-y.first+1,f=1;
if(lenx<leny)swap(x,y),swap(lenx,leny),f=-1;
if(Hash::Get(x.first,x.first+leny-1)==Hash::Get(y.first,y.second)){
if(leny*2>lenx)return -f;
return 0;
}
int l=0,r=leny,res=0;
while(l<=r){
int mid=(l+r)>>1;
if(Hash::Get(x.first,x.first+mid-1)==Hash::Get(y.first,y.first+mid-1))res=mid,l=mid+1;
else r=mid-1;
}
if(Hash::Val(x.first+res)<Hash::Val(y.first+res))return -f;
return f;
}
inline void pushup(int i,int l,int r){
pair<int,int> res=tree[i<<1][0];res.second=r;
for(auto it:tree[i<<1]){
it.second=r;
if(cmp(res,it)==1)res=it;
}
tree[i].clear();tree[i].push_back(res);
for(auto it:tree[i<<1|1])tree[i].push_back(it);
}
void build(int l=1,int r=n,int i=1){
if(l==r){
tree[i].push_back(make_pair(l,l));
return ;
}
int mid=(l+r)>>1;
build(l,mid,i<<1);build(mid+1,r,i<<1|1);
pushup(i,l,r);
}
void update(int fr,int to,int l=1,int r=n,int i=1){
if(fr>r||to<l)return ;
if(fr<=l&&to>=r)return ;
int mid=(l+r)>>1;
update(fr,to,l,mid,i<<1);update(fr,to,mid+1,r,i<<1|1);
pushup(i,l,r);
}
void query(int fr,int to,pair<int,int> &res,int l=1,int r=n,int i=1){
if(fr>r||to<l)return ;
if(fr<=l&&to>=r){
for(int j=tree[i].size()-1;~j;j--){
auto it=tree[i][j];it.second=to;
if(cmp(res,it)==1)res=it;
}
return ;
}
int mid=(l+r)>>1;
query(fr,to,res,mid+1,r,i<<1|1);query(fr,to,res,l,mid,i<<1);
}
}
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)scanf("%d",&Hash::a[i]);
Hash::init();
Seg::build();
while(q--){
int op;scanf("%d",&op);
if(op==1){
int l,r,d;scanf("%d%d%d",&l,&r,&d);
Hash::update(l,r,d);
Seg::update(l,r);
}
if(op==2){
int l,r;scanf("%d%d",&l,&r);
pair<int,int> res=make_pair(r,r);
Seg::query(l,r,res);
printf("%d\n",res.first);
}
}
return 0;
}
CS Academy Expected Tree Degrees
题意简述:\(n\) 个点的树,\([2,n]\) 的父亲从编号小于其的点种随便选,求每个点度数平方和期望。
平方和直接拆成选两个边,有公共端点期望,同边贡献为 \(2(n−1)\),剩下的对于 \(j<i\) 的点对 \((i,j)\),\(i\) 的父亲是 \(j\) 或者 \(j\) 的父亲才有贡献。
由于 \(j\) 的父亲是谁带来的贡献相同,都是 \(\dfrac{2}{i−1}\) ,而这里由于选择的是有序数对所以这部分得数要 \(×2\) 。
总的来说:
由于是浮点数形式输出,我们也可以设 \(dp[i][j]\) 表示有 \(i\) 个点的树中度数为 \(j\) 的点的期望个数,有:
看似是 \(O(n^2)\) 的,但当 \(j\ge 50\) 时,\(dp[i][j]\le 10^{-14}\) ,可以忽略,只需维护 \(j\le50\) 的部分即可。
点击查看代码
P6326 Shopping
考虑若连通块必须包含 \(x\),那么就对以 \(x\) 为根的有根树做树形背包。
设 \(f_{i,j}\) 为考虑了 \(\text{dfs}\) 序中 \([i,n]\) 对应的节点,体积为 \(j\) 的最大价值。转移分两种情况:一个是选 \(i\) 对应的节点,然后对该节点的物品跑多重背包。另一个是不选 \(i\) 对应的节点,然后从该节点子树外转移过来,这里可以在 \(\text{dfs}\) 序上表示转移的位置。
连通块不包含 \(x\) 的情况可以用点分治来递归处理。
复杂度为 \(O(nm\log d\log n)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int T,n,m,ans,tot,root,cnt;
int w[1005],c[1005],d[1005],f[1005][4005],siz[1005],mx[1005],out[1005],rev[1005];
bool vis[1005];
struct edge{
int to,nxt;
}e[1005];
int head[1005],edge_cnt;
inline void link(int from,int to){
e[++edge_cnt]={to,head[from]},head[from]=edge_cnt;
}
struct node{
int v,w;
}p[1005];
void dfs_root(int x,int fa){
siz[x]=1,mx[x]=0;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to;
if(vis[y]||y==fa) continue;
dfs_root(y,x),siz[x]+=siz[y];
mx[x]=max(mx[x],siz[y]);
}
mx[x]=max(mx[x],tot-siz[x]);
if(mx[x]<mx[root]) root=x;
}
void dfs_dfn(int x,int fa){
rev[++cnt]=x;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to;
if(vis[y]||y==fa)continue;
dfs_dfn(y,x);
}
out[x]=cnt;
}
void solve(int x){
vis[x]=1,cnt=0,dfs_dfn(x,0);
for(int i=cnt;i;i--){
int s=d[rev[i]]-1,num=0;
for(int j=1;j<=s;s-=j,j<<=1)p[++num]={w[rev[i]]*j,c[rev[i]]*j};
if(s)p[++num]={w[rev[i]]*s,c[rev[i]]*s};
for(int j=m;j>=c[rev[i]];j--)f[i][j]=f[i+1][j-c[rev[i]]]+w[rev[i]];
for(int k=1;k<=num;k++){
for(int j=m;j>=p[k].w;j--){
f[i][j]=max(f[i][j],f[i][j-p[k].w]+p[k].v);
}
}
for(int j=0;j<=m;j++)f[i][j]=max(f[i][j],f[out[rev[i]]+1][j]);
}
ans=max(ans,f[1][m]);
for(int i=1;i<=cnt;i++){
for(int j=0;j<=m;j++)f[i][j]=0;
}
int now=tot;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to;
if(vis[y])continue;
root=0,tot=siz[y];
if(siz[y]>siz[x])tot=now-siz[x];
dfs_root(y,x),solve(root);
}
}
inline void clear(){
edge_cnt=root=ans=0;
memset(vis,0,sizeof(vis));
memset(head,0,sizeof(head));
}
int main(){
scanf("%d",&T);
while(T--){
clear();
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
for(int i=1;i<=n;i++)scanf("%d",&c[i]);
for(int i=1;i<=n;i++)scanf("%d",&d[i]);
for(int i=1;i<n;i++){
int x,y;scanf("%d%d",&x,&y);
link(x,y);link(y,x);
}
tot=mx[0]=n;dfs_root(1,0);solve(root);
printf("%d\n",ans);
}
return 0;
}
[SDOI2017]苹果树
考虑 \(t−h≤k\) 的实际意义:我们可以免费选取一条到叶子的链(不是最长的一定不优),其他用树上依赖背包来付费获取,选取儿子的前提是选取父亲,背包大小为 \(k\) 。
考虑枚举每一个叶子到根节点的路径,并且删掉这条路径
这个树大概会被分为4个部分
- 链上免费取的部分。
- 链上付费取的部分。
- 树左边(这里暂时不理解没关系)的部分。
- 树右边的部分。
其中最为辣手的东西是第 \(2\) 个部分,因为这部分的点甚至不满足树形依赖关系,我们可以考虑拆点,一个点如果物品数大于 \(1\),拆成两个点,一个点是 \(i\),物品数只有一个,但是保留所有树上的连边关系,另一个是 \(i'\) 物品数是 \(a_i-1\) 不和任何其他点连边,只和 \(i\) 连边并且作为 \(i\) 的儿子出现,这样的话我们的 \(i'\) 就代表了这个点剩下的物品。
进一步,我们将选出的物品以免费最长链为分界分为三部分:
最长链左上方的是第一部分(\(\text{dfs}\) 序小于链底的点),最长链是第二部分,最长链右下方是第三部分(\(\text{dfs}\) 序大于链底的点)。
第一部分沿着正 \(\text{dfs}\) 序放物品,第三部分沿着逆 \(\text{dfs}\) 序放物品。
最后 \(O(k)\) 地枚举左右各选多少个,使用三部分的和更新答案即可,时间复杂度 \(O(nk)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int T;
int n,h;
int res,ctt,k;
int w[40005],a[40005],siz[40005];
int dfn1[40005],dfn2[40005],df1,df2;
int dp1[60000005],dp2[60000005];
int q1[1000005],q2[1000005],hed=1,til=0;
inline void dypr(int* dfn,int* dp){
for(int i=1;i<=ctt;i++){
int v=dfn[i];hed=1;til=1;q1[til]=q2[til]=0;
for(int j=1;j<=k;j++){
hed+=(q1[hed]<j-a[v])?1:0;
int val=dp[(i-1)*(k+1)+j]-j*w[v];
dp[i*(k+1)+j]=max(q2[hed]+j*w[v],dp[(i-siz[v])*(k+1)+j]);
while(hed<=til&&q2[til]<=val)til--;
q1[++til]=j;q2[til]=val;
}
}
}
vector<int> v[40005];
bool lf[40005];
int line[40005],nfd1[40005],nfd2[40005];
inline void clear_all(){
for(int i=0;i<=ctt;i++){
v[i].clear();lf[i]=line[i]=siz[i]=0;
}
for(int i=0;i<=(ctt+1)*(k+1);i++)dp1[i]=dp2[i]=0;
df1=df2=res=ctt=0;h=0;
}
void dfs1(int x){
siz[x]=1;
for(int i=0;i<v[x].size();i++){
dfs1(v[x][i]);siz[x]+=siz[v[x][i]];
}
dfn1[++df1]=x;nfd1[x]=df1;
}
void dfs2(int x){
for(int i=v[x].size()-1;i>=0;i--){
line[v[x][i]]=line[x]+w[v[x][i]];dfs2(v[x][i]);
}
dfn2[++df2]=x;nfd2[x]=df2;
}
int fa[40005];
inline void solve(){
scanf("%d%d",&n,&k);ctt=n;
for(int i=1;i<=n;i++){
scanf("%d%d%d",&fa[i],&a[i],&w[i]);
lf[fa[i]]=true;
}
for(int i=1;i<=n;i++){
v[fa[i]].push_back(i);
if(a[i]>1){
a[++ctt]=a[i]-1;
a[i]=1;w[ctt]=w[i];
v[i].push_back(ctt);
}
}
line[1]=w[1];
dfs1(1);dfs2(1);
dypr(dfn1,dp1);dypr(dfn2,dp2);
for(int i=1;i<=n;i++){
if(lf[i])continue;
for(int j=0;j<=k;j++){
res=max(res,dp1[(nfd1[i]-1)*(k+1)+j]+line[i]+dp2[(nfd2[i]-siz[i])*(k+1)+(k-j)]);
}
}
printf("%d\n",res);
}
int main(){
scanf("%d",&T);
while(T--)solve(),clear_all();
return 0;
}
[HDU6566] The Hanged Man
题意为给定 \(n\) 个点的树,每个节点为一个物品,有体积和价值,选物品必须满足不相邻,即选出一个独立集,求对于 \(∀i∈[1,m]\) ,容量为 \(i\) 时的背包最大价值的方案数。\((1⩽n⩽50,1⩽m⩽5000)\)
暴力就是直接树形背包,\(f_{i,j,0/1}\) 为在 \(i\) 的子树内,容量为 \(j\),是否选 \(i\) 的方案数,但复杂度为 \(O(nm^2)\),无法接受。
考虑用 \(\text{dfs}\) 序转移来优化,但是发现从 \(\text{dfs}\) 序中 \(i\) 转移到 \(i+1\) 时,若 \(i+1\) 对应的节点在 \(i\) 对应的节点的上方时,就可能不知道 \(i+1\) 的父亲选择的情况:

因此还需知道像图中 \(i+1\) 的父亲那样的转折点的选择情况,直接状压一个点到根节点路径上的所有转折点不现实,会被链卡成状态数为 \(O(2^n)\)。
考虑优化状态数,先进行重链剖分,剖分重链时优先遍历轻儿子,因为最后才遍历重儿子,所以一个点到根节点的所有转折点都是一条重链的链顶的父亲,那么再进行状压,状态数就为 \(O(2^{\log n})=O(n)\) 了。
设 \(f_{i,S,j}\) 为考虑到 \(\text{dfs}\) 序中第 \(i\) 个点,到根的转折点的状态为 \(S\),容量为 \(j\) 的方案数,转移是 \(O(1)\) 的,复杂度为 \(O(n^2m)\) 。
另外一个做法是进行点分治,将每次的分治中心作为转折点来状压,这样状态数也是 \(O(n)\) 的,如果不想进行状压,也可以在进入轻儿子时暴力枚举状态,分别递归,时间复杂度不变。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int T;
int n,m;
int ver[105],ne[105],head[55],tot;
inline void link(int x,int y){
ver[++tot]=y;
ne[tot]=head[x];
head[x]=tot;
}
int siz[55],son[55],fa[55];
void dfs1(int x,int fi){
siz[x]=1;fa[x]=fi;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fi)continue;
dfs1(u,x);siz[x]+=siz[u];
if(siz[u]>siz[son[x]])son[x]=u;
}
}
int w[55],v[55];
pair<long long,long long> dp[2][55][5005],tmp[2][55][5005];
inline pair<long long,long long> cmp(pair<long long,long long> x,pair<long long,long long> y){
if(x.first==y.first)return make_pair(x.first,x.second+y.second);
return x.first<y.first?y:x;
}
inline pair<long long,long long> operator +(pair<long long,long long> x,long long y){
return make_pair(x.first+y,x.second);
}
void dfs2(int x,int fi,int cnt){
for(int i=0;i<=m;i++)tmp[0][cnt][i]=dp[0][cnt][i];
for(int i=0;i<=m;i++)tmp[1][cnt][i]=dp[1][cnt][i];
int lim=cnt;
for(int i=0;i<=m;i++)dp[0][cnt][i]=make_pair(-1e18,0);
for(int i=0;i<=m;i++)dp[1][cnt][i]=tmp[1][cnt][i];
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fa[x]||u==son[x])continue;
for(int j=0;j<=m;j++)dp[0][lim+1][j]=cmp(dp[0][lim][j],dp[1][lim][j]);
for(int j=0;j<=m;j++)dp[1][lim+1][j]=make_pair(-1e18,0);
dfs2(u,x,lim+1);lim+=siz[u];
}
if(son[x]){
for(int j=0;j<=m;j++)dp[0][lim+1][j]=cmp(dp[0][lim][j],dp[1][lim][j]);
}
for(int i=0;i<=m;i++)dp[0][cnt][i]=tmp[0][cnt][i];
for(int i=0;i<=m;i++)dp[1][cnt][i]=make_pair(-1e18,0);
lim=cnt;
for(int i=head[x];i;i=ne[i]){
int u=ver[i];
if(u==fa[x]||u==son[x])continue;
for(int j=0;j<=m;j++)dp[0][lim+1][j]=cmp(dp[0][lim][j],dp[1][lim][j]);
for(int j=0;j<=w[u];j++)dp[1][lim+1][j]=make_pair(-1e18,0);
for(int j=w[u];j<=m;j++)dp[1][lim+1][j]=dp[0][lim+1][j-w[u]]+v[u];
dfs2(u,x,lim+1);lim+=siz[u];
}
if(son[x]){
for(int j=0;j<=m;j++)dp[0][lim+1][j]=cmp(dp[0][lim+1][j],cmp(dp[0][lim][j],dp[1][lim][j]));
for(int j=0;j<w[son[x]];j++)dp[1][lim+1][j]=make_pair(-1e18,0);
for(int j=w[son[x]];j<=m;j++)dp[1][lim+1][j]=cmp(dp[0][lim][j-w[son[x]]],dp[1][lim][j-w[son[x]]])+v[son[x]];
dfs2(son[x],x,lim+1);
}
for(int i=0;i<=m;i++)dp[0][cnt][i]=tmp[0][cnt][i];
for(int i=0;i<=m;i++)dp[1][cnt][i]=tmp[1][cnt][i];
}
inline void solve(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d%d",&w[i],&v[i]);
for(int i=1;i<n;i++){
int x,y;scanf("%d%d",&x,&y);
link(x,y);link(y,x);
}
dfs1(1,1);
for(int i=0;i<=m;i++)dp[0][1][i]=make_pair(-1e18,0);
for(int i=0;i<=m;i++)dp[1][1][i]=make_pair(-1e18,0);
dp[0][1][0]=make_pair(0,1);dp[1][1][w[1]]=make_pair(v[1],1);
dfs2(1,1,1);
for(int i=1;i<m;i++)printf("%lld ",cmp(dp[0][n][i],dp[1][n][i]).second);
printf("%lld\n",cmp(dp[0][n][m],dp[1][n][m]).second);
// for(int i=1;i<=m;i++)printf("%d %d %d %d\n",dp[0][n][i].first,dp[0][n][i].second,dp[1][n][i].first,dp[1][n][i].second);
for(int i=1;i<=n;i++)head[i]=0;tot=0;
for(int i=1;i<=n;i++)siz[i]=0;
for(int i=1;i<=n;i++)son[i]=0;
}
int main(){
scanf("%d",&T);
for(int i=1;i<=T;i++){
printf("Case %d:\n",i);
solve();
}
return 0;
}
[Gym102341G] Gurdurr
\(N\) 层积木, 每层由三个长方体构成,两个人博弈, 轮流卸下一块积木, 并保持积木的稳定,积木稳定定义:
◦ 每层都有至少一块积木。
◦ 如果一层中只有一块, 那么是中间那块。
◦ 没有相邻的两层都只有一块。
◦ \(30000\) 组询问, 每次给定 \(n <= 20\) 和 \(n\) 层积木的初始状态, 问先手必胜必败。
观察状态, \(\text{I}\) 表示积木, \(\text{.}\) 表示没有积木
那么有 \(\text{III, II., .II, I.I, .I.}\) 五种状态, 其中第二三种相同, 第四五种不可操作. 对于游戏来说, 出现四五种状态即可认为分为两个子游戏 --- \(\text{SG}\) 函数 。
剩下 \(2\) 种不同状态, 所以记录 \(f[s][0/1][0/1]\) 表示局面为 \(s\), 上端和下端是 \(1\) 个还是 \(2\) 个. 枚举操作位置, 算出 \(\text{SG}\) 即。
点击查看代码
[Gym102341B] Bulbasaur
先利用最大流最小割定理将要求的转化为最小割,然后就可以转化为删掉最少的点使得两层不连通。
我们先考虑 \([1,i]\) 层,设 \(f_{s,j}\)表示使得第 \(i\) 层有且仅有 \(S\) 中的点能够到达 \(j\) 层,最少需要删掉的点数。
显然 \(f_{s,j}\) 关于 \(j\) 单调,并且 \(f_{s,j}∈[0,m]\) 。
那么我们升序枚举 \(i\),然后对于同一个 \(s\),维护值不相同的 \(f_{s,j}\) 的 \(j\) 之间的分界线。转移是非常简单的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,to[10];long long ans;
struct node{
int pos[10];
node(){memset(pos,0,40);}
inline int& operator[](int x){
return pos[x];
}
}f[1<<9],t[1<<9];
inline void merge(node&p,node q){
if(p[0]>q[0])swap(p,q);
for(int i=m;~i;i--)if(q[i]==q[0])q[i]=p[0];
for(int i=1;i<=m;i++)p[i]=max(p[i],q[i]);
}
inline node up(node x){
for(int i=m;i;--i)x[i]=x[i-1];
return x;
}
inline int get(){
char c=getchar();
while(!isdigit(c))c=getchar();
return c&15;
}
inline int cal(int s){
int res=0;
for(int i=0;i<m;++i)if(s>>i&1)res|=to[i];
return res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<1<<m;i++)for(int j=0;j<=m;j++)f[i][j]=j<=m-__builtin_popcount(i)?1:n+1;
for(int i=2;i<=n;i++){
memset(to,0,m<<2);
for(int j=0;j<(1<<m);j++)for(int k=0;k<=m;k++)t[j][k]=n+1;
for(int j=0;j<m;j++)for(int k=0;k<m;k++)if(get())to[j]|=1<<k;
for(int j=0;j<(1<<m);j++)merge(t[cal(j)],f[j]);
swap(f,t);
for(int j=(1<<m)-1;j;j--){
node r=up(f[j]);
for(int k=0;k<m;k++)if(j>>k&1)merge(f[j^1<<k],r);
}
for(int j=0;j<(1<<m);j++)for(int k=0;k<=m-__builtin_popcount(j);k++)f[j][k]=min(f[j][k],i);
for(int j=1;j<=m;j++)ans+=i-f[0][j];
}
printf("%lld",ans);
return 0;
}
[AGC036F] Square Constraints
题目的要求相当于:

在两个圆之间的圆环区域中放置 \(2n-1\) 个车,要求车都放在整点上,且互不攻击,求方案数,任意模数。
弱化
如果里面的圆不存在,此时方案数是多少?
为了方便,记 \(L_i=\lceil\sqrt{n^2-i^2}\rceil\),\(R_i=\lfloor\sqrt{4n^2-i^2}\rfloor\) 。

此时可以在圆内画出图中的几条线段。
显然,每一个车放在一条线段上,并且不能在同一横排。
那么就先考虑最短线段(即第 \(2n-1\) 条线段)上面的车,此时有 \(R_{2n-1}+1\) 种方案。
在决策完这个车放在哪里之后,剩下的每一条线段都会少一个可以放的位置。
对第二短的线段重复一遍这个过程,可以发现也会让剩下的每一条线段少一个可以放的位置。
因此,如果设 \(R\) 排序后的数组为 \(R'\) ,那么方案数就是:
容斥
既然对于没有下限的问题有了一个快速解法,那么这个解法是否有可能应用到有下限的问题中呢?
不满足要求的方案数也是前缀,这引诱我们进行容斥。
如果恰有 \(k\) 个元素的上界是 \(L_i-1\),那么这个方案数对答案的贡献就是 \((-1)^k\times f_k\) 。
考虑 \(\text{DP}\) 出 \(f_k\) 。
DP
因为现在上界是 \(L_i-1\),所以 \([0,n)\) 内的元素取关键字为 \(L_i-1\),\([n,2n)\) 内的元素取关键字为 \(R_i\) 进行排序。
现在我们得到了一个排好序的数组,就可以进行 \(\text{DP}\) 了。
设 \(f_{i,j}\) 为 \(\text{DP}\) 到前 \(i\) 个,并且有 \(j\) 个选择 \(L-1\) 作为上界的元素的总方案数。
显然有 \(f_{0,0}=1\) 。
下面考虑每一个元素。
如果这个元素没有下界,即原本处于区间 \([n,2n)\) 之间,那么它的方案数可以这么考虑:
原本有 \(R_i+1\) 个方案;
它前面的选择 \(L-1\) 的,由于排序保证了它小于 \(R_i\) ,所以每一个限制掉一个方案。这类会限制掉 \(j\) 个方案;
它前面的没有下界的,同样是由于排序;这个需要在 \(\text{DP}\) 过程中统计,设其为 \(c_1\) 。
所以可行的决策数为 \(R_i+1-j-c_1\) 。有转移:
然后考虑有下界的情况。这类要分开讨论。
如果取上界为 \(L_i-1\),则:
原本有 \(L_i\) 个方案;
它前面的选择 \(L-1\) 的和没有下界的,限制住 \(c_1+j\) 个方案。
可行决策有 \(L_i-c_1-j\) 个。有转移:
如果取上界为 \(R\),则:
原本有 \(R_i+1\) 个方案;
关键性质:由于在 \([0,n)\) 内,最小的 \(R\) 是 \(\sqrt 2n\) 大于最大的 \(L\),所以任何有下界且选择 \(L-1\) 的元素都一定会影响这里的决策。
由于这个性质的存在,所以这一类的限制为 \(k\)。
此时的 \(R\) 大于所有满足 \(i\in [n,2n)\) 的 \(R_i\) ,每一个都产生限制,限制为 \(n\)。
如果有下界的取上界为 \(R\),那么在这个元素之前的也会影响决策。为了统计这个方案数,可以统计之前有下界的元素数量,设其为 \(c_2\) ,则这里限制为 \(c_2-j\) 。
故可行决策有 \(R_i+1-n-k-c_2+j\) 个。转移:
答案即为 \(f_{2n,k}\) 。
\(\text{DP}\) 的复杂度为 \(O(n^2)\),前面还要枚举一个 \(k\),所以最终时间复杂度 \(O(n^3)\),空间复杂度 \(O(n^2)\),可以通过本题。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,md,dp[505][505];
pair<int, int> p[505];
inline void init(){
for(int i=0;i<n;i++){
p[i+1].first=ceil(sqrt(n*n-i*i))-1;
p[i+1].second=floor(sqrt(4*n*n-i*i));
if(p[i+1].second>2*n-1)p[i+1].second=2*n-1;
}
for(int i=n;i<2*n;i++){
p[i+1].first=floor(sqrt(4*n*n-i*i));
if (p[i+1].first>2*n-1)p[i+1].first=2*n-1;
p[i+1].second=0;
}
sort(p+1,p+2*n+1);
}
inline int calc(int k){
memset(dp,0,sizeof(dp));
dp[0][0]=1;
int lim=0,cnt=0;
for(int i=1;i<=2*n;i++){
if(p[i].second==0){
for(int j=0;j<=lim;j++)dp[i][j]=(dp[i][j]+1ll*dp[i-1][j]*(p[i].first-cnt-j+1)%md)%md;
cnt++;
}
else{
for(int j=0;j<=lim;j++){
dp[i][j]=(dp[i][j]+1ll*dp[i-1][j]*(p[i].second+1-n-k-lim+j)%md)%md;
dp[i][j+1]=(dp[i][j+1]+1ll*dp[i-1][j]*(p[i].first-cnt-j+1)%md)%md;
}
lim++;
}
}
return dp[2*n][k];
}
int main(){
scanf("%d%d",&n,&md);
init();
int res=0;
for(int i=0;i<=n;i++){
if(i&1)res=(res-calc(i)+md)%md;
else res=(res+calc(i))%md;
}
printf("%d\n",res);
return 0;
}
CF1142D Foreigner
可以用刷表法来构造所有合法的数字,写成代码是这样的:
for (int i = 1; i <= 9; i++) q[++t] = i;
while (1) {
int u = q[h++];
for (int i = 0; i < h % 11; i++) q[++t] = q[h] * 10 + j;
}
考虑计算往数列中第 \(i\) 个数后面接一个 \(c\),得到的数字的排名是多少,由于这个数列是根据生成顺序递增的,所以我们只需要计算比它小的数的个数:
我们发现后面可以接的数字只与标号对 \(11\) 取模的值有关,我们尝试把整个柿子都放到 \(\bmod 11\) 的意义下,这样就能把中间的 \(k\%11\) 去掉了。
这般之后,我们发现数字的标号,其实只需要维护 \(\bmod 11\) 意义下的值就可以了。
我们设 \(dp[i][j]\) 表示末尾数位为 \(s[i]\),标号在 \(\bmod 11\) 意义下为 \(j\),且能匹配上以 \(i\) 为结尾的子串的数的个数。
我们记上面那个值为 \(\text{nxt}(i,j)\),就是标号为 \(i\) 的后面怼个 \(j\) 的数的标号,那么转移就有:
如果 \(s[i]>0\) 的话单独一个数字也是可以匹配的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
long long dp[100005][15];
char s[100005];
inline int nxt(int x,int c){
return (x*(x-1)/2+c+10)%11;
}
int main(){
scanf("%s",s+1);n=strlen(s+1);
long long res=0;
for(int i=1;i<=n;i++){
for(int j=s[i]-'0'+1;j<=10;j++)dp[i][nxt(j,s[i]-'0')]+=dp[i-1][j];
if(s[i]!='0')dp[i][s[i]-'0']++;
for(int j=0;j<=10;j++)res+=dp[i][j];
}
printf("%lld\n",res);
return 0;
}
[TJOI2018]游园会
考虑 \(\text{dp}\) 套 \(\text{dp}\) ,如果我们直接定义 \(f_{i,j,l}\) 表示考虑到第 \(i\) 位,与 \(s\) 的 \(\rm lcs\) 为 \(j\),与 \(\mathtt{NOI}\) 的匹配长度为 \(l\) 的字符串个数,那么 \(\text{lcs}\) 在每个状态的值是未知的,无法完成转移。所以我们不妨考虑将整个 \(\rm lcs\) 数组传入状态。
显然传入整个数组是不现实的,我们尝试观察 \(\rm lcs\) 的转移方法:
其中 \(\text{lcs}_{i,j}\) 表示当前考虑到第 \(i\) 位,与 \(s\) 串匹配到第 \(j\) 位的最长公共子序列长度。
为此,我们可以得到几条优化:
转移中只涉及到了第 \(i-1\) 行和第 \(i\) 行的状态,所以我们只需要存储一行状态即可。
注意到 \(\text{lcs}_{i,j}-\text{lcs}_{i,j-1}\in\{0,1\}\),所以我们可以通过状压差分数组来存储一行的信息。
这样我们重新定义状态:\(f_{i,state,l}\) 表示考虑到第 \(i\) 位,\(\text{lcs}\) 数组状态为 \(\text{state}\),与 \(\mathtt{NOI}\) 的匹配长度为 \(l\) 的方案数。之后我们枚举第 \(i\) 位的字符,转移就很好想了。
状态数 \(O(n2^k)\),转移 \(O(k)\)(因为要求出新的 \(\text{state}\)),总时间复杂度 \(O(nk2^k)\) 。使用一些剪枝就可以通过此题。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int md=1e9+7;
int n,k;
int dp[2][1<<15][3],cnt[1<<15],m[305],tmp[2][17],ans[17];
char s[17];
inline void decode(int S){
for(int i=0;i<k;i++)tmp[0][i+1]=(S>>i&1);
for(int i=1;i<=k;i++)tmp[0][i]+=tmp[0][i-1];
return ;
}
inline int encode(){
int S=0;
for(int i=1;i<=k;i++){
int now=tmp[1][i]-tmp[1][i-1];
S^=now*(1<<(i-1));
}
return S;
}
inline void trans(int cur,int S,int c,int p,int x){
if((p==2&&c==2)||x==0)return ;
int nxt=(c==0)?1:0;
if(p==0&&c==0)nxt=1;
else if(p==1&&c==1)nxt=2;
decode(S);tmp[1][0]=0;
for(int i=1;i<=k;i++){
if(m[s[i]]==c)tmp[1][i]=tmp[0][i-1]+1;
else tmp[1][i]=0;
tmp[1][i]=max(tmp[1][i],max(tmp[0][i],tmp[1][i-1]));
}
int ns=encode();
dp[cur][ns][nxt]=(dp[cur][ns][nxt]+x)%md;
return ;
}
int main(){
scanf("%d%d",&n,&k);
scanf("%s",s+1);
m['N']=0;m['O']=1;m['I']=2;
int cur=0;
dp[cur][0][0]=1;
for(int i=1;i<=n;i++){
cur=cur^1;
memset(dp[cur],0,sizeof(dp[cur]));
for(int j=0;j<(1<<k);j++){
for(int p=0;p<3;p++){
trans(cur,j,p,0,dp[cur^1][j][0]);
trans(cur,j,p,1,dp[cur^1][j][1]);
trans(cur,j,p,2,dp[cur^1][j][2]);
}
}
}
cnt[0]=0;
for(int i=1;i<(1<<k);i++)cnt[i]=cnt[i>>1]+(i&1);
for(int i=0;i<(1<<k);i++){
for(int p=0;p<3;p++)ans[cnt[i]]=(ans[cnt[i]]+dp[cur][i][p])%md;
}
for(int i=0;i<=k;i++)printf("%d\n",ans[i]);
return 0;
}
[ZJOI2019]麻将
首先需要解决一个子问题就是怎样判断一个牌集拥有一个能够胡的子集。
第一个条件:四个面子+一个对子
一个结论:相同花色顺子最多 \(2\) 个,因为三个相同的顺子可以等价给三个不同的刻子,而且对答案没有影响
首先不考虑对子的情况,定义状态 \(dp[i][j][k]\) 表示当前处理完 \([1,i]\) 花色,其中 \((i-1,i)\) 有 \(j\) 对,\(i\) 剩下有 \(k\) 个下最大的面子数
注意!我们都是先满足顺子,然后满足刻子
那么考虑加入 \(i+1\),我们枚举下一个状态还剩下 \(t\) 个 \(i+1\),因为先满足顺子,所以这里假定顺子已经填满了,增加了 \(i\) 的贡献,此时还剩下的若干个相同花色的,我们就考虑全部转化成刻子。
所以状态转移方程为:\(dp[i+1][j][k]=\max\{ i+dp[i][j][k]+\lfloor \dfrac{remain}3\rfloor\}\)
但是题目中还需要有一个对子,所以我们把状态定义为 \(dp[0/1][i][j][k]\),其中的 \(i,j,k\) 意义不变,新增一维表示是否已经出现对子。\(dp[0]\) 和 \(dp[1]\) 内部的转移还是和上面一样。考虑 \(dp[0]\) 和 \(dp[1]\) 之间的转移,如果我们当前加入花色的个数 \(\geq 2\),我们就可以先消耗两个花色,然后从 \(dp[0]\) 转移到 \(dp[1]\) 。
第二个条件:七个对子
因为状态相对于第一个条件独立,所以直接考虑新开一维 \(cnt\),表示不同花色的对子个数。
注意!一定是花色不同,即一次修改只能修改 \(1\)
子任务实现
可以开一个结构体,方便处理。(因为我们需要用 \(\mathrm{map}\) 去重)
构造自动机
考虑到这个状态的总数应该不会太多,所以我们考虑先预处理出自动机。
因为有限状态,所以通过搜索来得到自动机的复杂度是正确的。
构造的时候,我们对于当前状态,枚举下一个牌放多少张来转移即可。
这里实测:本质不同的状态数有 \(3956\) 个,本质不同的不胡状态数有 \(2092\) 个。
\(\text{DP}\) 统计方案数
构造了自动机后,我们就要统计方案数了。
定义 \(f[i][j][k]\) 表示当前考虑前 \(i\) 个花色,摸了 \(j\) 张牌,当前的胡牌状态为 \(k\) 的方案数。
考虑第 \(i+1\) 张牌摸的数量 \(t\)。
统计答案
如何统计答案,我们先回顾一下原题:
题意:求出存在能胡子集的期望步数。
设 \(P(i)\) 为走了 \(i\) 就胡了的概率,则答案 \(Ans=\sum_{i=0}^{\infty}\limits P(i)\times i\)
转化 \(P_1(i)=\sum_{j=i}^{\infty}\limits P(i)\)
代入原式得到了 \(Ans=\sum_{i=1}^{\infty}\limits P_1(i)\)
重视一下 \(P_1(i)\) 的含义,我们可以发现 \(P_1(i)\) 就代表 \(i\) 及以后胡的概率,也就是前 \(i-1\) 次不胡的概率(因为后面延伸到无限,所以只要满足前 \(i-1\) 次不胡,根据题目中所说不难发现 \(P\) 的权值就是理论上的最早胡牌巡目数,那么后面一定能胡)
所以题目的答案又被转化成了不能胡的概率和。
我们用式子来表示:
\(g(i)\) 就是手中一共有 \(i\) 张牌,还不能胡的方案数,\(sum(i)\) 表示 \(i\) 张牌的总方案数,时间复杂度是 \(\mathcal O(3956\times n\times m)\) 。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
struct S{
int a[3][3];
S(){memset(a,-1,sizeof(a));}
inline int* operator [](int t){return a[t];}
inline bool operator <(const S &b)const{
for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(a[i][j]!=b.a[i][j])return a[i][j]<b.a[i][j];
return 0;
}
inline S operator +(int num){
S res;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
if(a[i][j]==-1)continue;
for(int t=0;t<3&&i+j+t<=num;t++)res[j][t]=max(res[j][t],min(4,a[i][j]+i+(num-i-j-t)/3));
}
}
return res;
}
inline S operator +(S b){
S res;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++)res[i][j]=max(a[i][j],b[i][j]);
}
return res;
}
};
struct state{
pair<S,S> s;int cnt;
state(){
s=make_pair(S(),S());
s.first[0][0]=cnt=0;
}
inline bool operator <(const state &b)const{
if(cnt!=b.cnt)return cnt<b.cnt;
return s<b.s;
}
inline state operator +(int num){
state res=*this;res.cnt=min(7,cnt+(num>=2));
res.s.second=res.s.second+num;
if(num>=2)res.s.second=res.s.second+(s.first+(num-2));
res.s.first=res.s.first+num;
return res;
}
inline bool check(){
if(cnt>=7)return 1;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++)if(s.second[i][j]>=4)return 1;
}
return 0;
}
}g[4005];
map<state,int> id;
int tot;
bool ed[4005];
void dfs(state x){
if(id.count(x))return;
id[x]=++tot;
ed[tot]=x.check();g[tot]=x;
for(int i=0;i<=4;i++)dfs(x+i);
}
const int md=998244353;
int n;
int a[105],C[5][5],trans[4005][5],dp[105][405][4000];
inline int pwr(int x,int y){
int res=1;
while(y){
if(y&1)res=1ll*res*x%md;
x=1ll*x*x%md;y>>=1;
}
return res;
}
inline void init(){
dfs(state());
for(int i=1;i<=tot;i++){
for(int j=0;j<=4;j++)trans[i][j]=id[g[i]+j];
}
C[0][0]=1;
for(int i=1;i<=4;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)C[i][j]=(C[i-1][j-1]+C[i-1][j])%md;
}
}
int main(){
scanf("%d",&n);init();
for(int i=1;i<=13;i++){
int x,y;scanf("%d%d",&x,&y);
a[x]++;
}
dp[0][0][1]=1;
for(int i=0;i<n;i++){
for(int j=0;j<=4*i;j++){
for(int s=1;s<=tot;s++){
if(!dp[i][j][s])continue;
for(int t=a[i+1];t<=4;t++)dp[i+1][j+t][trans[s][t]]=(dp[i+1][j+t][trans[s][t]]+1ll*dp[i][j][s]*C[4-a[i+1]][t-a[i+1]])%md;
}
}
}
int res=0;
for(int i=13;i<=4*n;i++){
int all=0,sum=0;
for(int j=1;j<=tot;j++){
all=(all+dp[n][i][j])%md;
if(!ed[j])sum=(sum+dp[n][i][j])%md;
}
res=(res+1ll*sum*pwr(all,md-2))%md;
}
printf("%d\n",res);
return 0;
}


