p_b_p_b 杂题选讲
[ARC119F] AtCoder Express 3
[ARC117F] Gateau
考虑二分答案,对前缀和建差分约束 \(\text{check}\) ,但是用 \(\text{spfa}\) 判断负环是 \(O(n^2)\) 的,妥妥地 \(\text{TLE}\) 掉。仔细观察这张图,实际上它是很有规律的:

这是在一条链的基础上给 \(i\) 和 \(i+n\) 连了一条双向边,我们从 \(2\times n\) 向 \(n\) 扫,同时考虑 \((i)\to (i-n)\to (i-n-1)\to (i-1)\) 这样路径的影响,在不存在负环的情况下,扫描一次后可以求出 \(2\times n\to n\) 的最短路,两次即可算出 \(n\to 0\) 的最短路,扫描第三次时如果还能更新,说明存在负环。
代码建的是反图,判断有没有正环:
点击查看代码
【UR #7】水题走四方
容易发现,一定有一种方案使得一个人始终被传送,另一个始终不被传送,称被传送的那个为分身,不被传送的为本体。
而最终的方案一定是本体走一条链,分身走完链上的所有支路。
但是两个点可以同时移动,也就是说令 \(dp[x]\) 表示本体从根走到 \(x\) 处的答案,\(dp[x]\) 不一定是从 \(x\) 处转移过来的,记一个 \(top[x]\) 表示离 \(x\) 最近的祖先使得它含有一条不在 \(x\) 这个子树内的深度大于 \(x\) 的链,转移时从 \(top[x]\) 和 \(fa[x]\) 分别转移即可。
点击查看代码
#177. 新年的腮雷
正着不好做,考虑逆向这个过程,即二分最后树根的点权,然后把树上的叶子拆分。最后我们只需要判定是否 \(a\) 中每个元素都能匹配上比它大的元素即可。
不妨将 \(a,b\) 都排序,考虑更一般的集合 \(S,T\),\(|S|≤|T|\),\(|S|≡|T|(\bmod m−1)\),问 S 能不能拆成 T。
-
若 \(\max S<\max T\),无解。
-
若 \(\max T≤\max S<b_1+\max T\),将 \(S\) 的最大元拆掉就不能对应了,所以与 \(T\) 的最大元对应的元素不能拆,找一个 \(\text{lower_bound}\) 匹配即可。
-
若 \(\max S≥b_1+\max T\),则 \(\max S\) 拆掉不劣。
模拟这个过程即可,时间复杂度 \(O(n\log n\log V)\) 。
[CodeChef] Destructive Nim
不妨枚举 \(B\) 第一次选哪个,然后游戏规则就变成:
- 从当前石子堆拿走若干个,然后选定下一次的石子堆。
- 如果拿完之后没有石子了那么获胜。
考虑拿完当前这一堆。如果拿完之后是必胜的那么就赢了。否则,可以拿到只剩一个,然后强迫对方还是拿这一堆,那么就还是赢了。
所以只要当前这堆不是只剩一个就赢了。
所以判一下 \(1\) 的个数的奇偶性,以及是否存在非 \(1\) 的堆即可。
点击查看代码
[AGC040F] Two Pieces
不妨令 \(1\) 为坐标较大的棋子,\(2\) 为另一个,令 \(A\geqslant B\) 。
把 \(2\) 的坐标和 \(1\) 的坐标作为数对,看作二维平面上的一个点。我们画出直线 \(y=x\),那么让 \(1\) 走一步就是向右(记为操作 \(1\)),让 \(2\) 走一步就是向上(记为操作 \(2\)),让 \(2\) 跳到 \(2\) 就是跳到直线上(记为操作 \(3\)),且操作 \(2\) 不能碰触直线,最后要到达 \((A,B)\) 。
操作 \(3\) 次数为 \(0\) 的时候很容易处理,可以类似卡特兰数使用折线法。(注意是不能碰触直线,所以要将坐标系整体左移一格)
我们发现跳到直线上很难处理,我们将操作 \(3\) 转化成将直线移到当前位置上。记最后一次操作的坐标为 \((x_0,y_0)\),那么我们的终点就应该是 \((A-1,B-(x_0-y_0))\) 。(\(A-1\) 的原因上面说了)
但是还是很难考虑,我们考虑在确定了 \((x_0-y_0)\) 以及行走出来的格路之后,将操作 \(3\) 插入操作序列。观察可以得到,对于让直线变为 \(y=x-k\) 的操作 \(3\),它的插入位置一定只能是这个直线与格路的最后一个交点(容易发现满足条件的操作 \(3\) 即 \(0,1,\cdots,k\)),于是枚举 \(x_0-y_0\),然后插板法计算即可,复杂度 \(O(n)\) 。
点击查看代码
[AGC026F] Manju Game
博弈题可以先想一个简单一点的策略,然后再修正他。
最简单的策略就是先手选择边界上的权值,当先手做出决定的时候,游戏就已经结束了。但是这种策略其实也有可取之处,就是后手无法做出选择,主动权全在先手手上。
这启发我们进行关于主动权的讨论,而讨论主动权势必涉及到 \(n\) 的奇偶性,所以按照 \(n\) 的奇偶性分类讨论。
如果 \(n\) 是偶数,那么如果先手选择非边界,会把剩下的点分成奇数段和偶数段。那么如果后手选择在偶数段操作,在和获得简单策略不优权值的情况下,先手会失去主动权,所以先手不会再非边界操作,这说明我们可以直接应用简单策略。
如果 \(n\) 是奇数,那么如果先手选择奇数点,会把剩下的点分成两个偶数段,类比上面的讨论先手不会这样做。所以先手要么应用简单策略,要么选取一个偶数点操作。
考虑先手选取偶数点的情况,后手会消去一个区间,然后问题会向另一个递归,此时主动权仍然在先手手上。注意这个过程构成了一个树形结构。那么问题可以转化成,先手先钦定一个二叉树,上面的节点都是偶数节点,后手可以自由选择走到哪个叶子。
所以我们要最大化 “走到所有叶子对应的最小赚取量”,其中赚取量定义为:从根走到这个叶子剩下的区间中,奇数位置减去偶数位置的权值(因为叶子就是问题的出口了,所以这个区间应该直接应用简单策略,赚取量就是和直接取偶数位置的差值)
考虑二分最大赚取量 \(x\),我们再把问题放在序列上来。问题变成了求是否存在一个偶数点的划分方案,使得相邻两个偶数点之间的 “奇数位置减去偶数位置的权值” 都大于 \(x\)(特别地,序列的左右边界视为有两个偶数点)
考虑贪心,从左往右扫描,维护一个最优划分点 \(j\);如果当前点 \(i\) 和 \(j\) 划分后它们之间满足条件,那么看看 \(s[i]\) 是否比 \(s[j]\) 小(\(s\) 是奇数位置减去偶数位置权值的前缀和),如果是的话,把 \(i\) 作为最优划分点。
时间复杂度 \(O(n\log n)\) 。
点击查看代码
[ARC122F] Domination
CF1033G Chip Game
考虑给定 \(a,b\) 怎么做。
非常不显然的是,对于所有 \(v'_i\equiv v_i\mod (a+b)\) 构成的局面 \(S'\) ,它与所有 \(v_i\) 构成的局面 \(S\) 本质上是相同的。
因为无论被模掉之后的序列先手必胜还是后手必胜,赢家都可以在输家操作多余部分时跟着操作,使得整个序列向取模后的状态靠拢。
值得注意的是,\(A\) 赢的情况和 \(B\) 赢的情况是对称的,而且指的是无论他是否先手.这样用总方案数 \((m^2)\) 减去先/后手必胜的情况再除以 \(2\) 即可。
枚举 \(X=a+b\) ,将 \(v\) 排序,然后对 \(a\) 的值分类讨论。
显然,选的值越小越优。
如果存在 \(v_i\) 满足 \(a\leq v_i<b\),那么无论如何 \(a\) 必胜。
如果存在 \(v_i\) 满足 \(2a\leq v_i\),那么 \(a\) 同样必胜。
那么需要满足的条件就是不存在以上两种情况,\(\geq a\) 的 \(v_i\) 数量的奇偶性决定胜负。
点击查看代码
[IOI2015] sorting
设 E 的一次操作为 \(E\) , A 的一次操作为 \(A\) , 那么最终的操作序列应该为 \(E_1A_1E_2A_2E_3A_3E_4A_4\cdots\) 。
发现一组 \(AE\) 操作必定可以转化为一组 \(EA'\) , 意思是存在一个 \(E\) 先操作一步, \(A\) 再操作一步的效果与 \(A\) 先操作一步, \(E\) 再操作一步的效果相同, 并且对于确定的 \(E\) , \(A\) 和 \(A'\) 是一一对应的.
于是我们不妨把所有 \(A\) 移动到 \(E\) 的后面, 构造一个这样的操作序列 \(E_1E_2E_3E_4\cdots A'_1A'_2A'_3A'_4\) , 并通过这个序列还原出原序列。
考虑从 \(A'\) 如何还原为 \(A\) , 对于已知的 \(A,E\), 考虑使 \(AE=EA'\) 的 \(A'\) , 有如下几种情况:
-
\(A=(a,b),E=(c,d)\) , 则 \(A'=(a,b)\) 。
-
\(A=(a,b),E=(a,c)\) , 则 \(A'=(b,c)\) 。
-
\(A=(a,b),E=(a,b)\) , 则 \(A'=(a,b)\) 。
不难发现: \(A'\) 还原到 \(A\) , 如果 \(A'\) 与 \(E\) 中有相同的位置, 那么就把这个位置变成 \(E\) 中的另一个位置。
暴力还原原操作序列是 \(\mathcal O(n^2)\) 的(一个 \(A'\) 需要与 \(\mathcal O(n)\) 个 \(E\) 交换), 不能承受, 考虑优化。
发现 \(A'\) 与 \(E=(a,b)\) 交换等价于把 \(a\) 映射到 \(b\) , \(b\) 映射到 \(a\) , 并且这个映射是可以合并的。于是的到这样一个算法: 从后向前扫 \(E\) 序列, 边维护当前 \(E\) 后缀对应的映射, 边计算出插在当前 \(E\) 前面的 \(A\) (详见代码). 这个部分的复杂度是 \(\mathcal O(n)\) 。
时间复杂度 \(\mathcal O(n\log n)\) 。
点击查看代码
[IOI2015] Towns
考虑求半径显然先求直径,使用 \(2n−2\) 次询问直接找出答案。
然后考虑我们对于每一个点,其实它与直径上的距离是可以计算出来的。
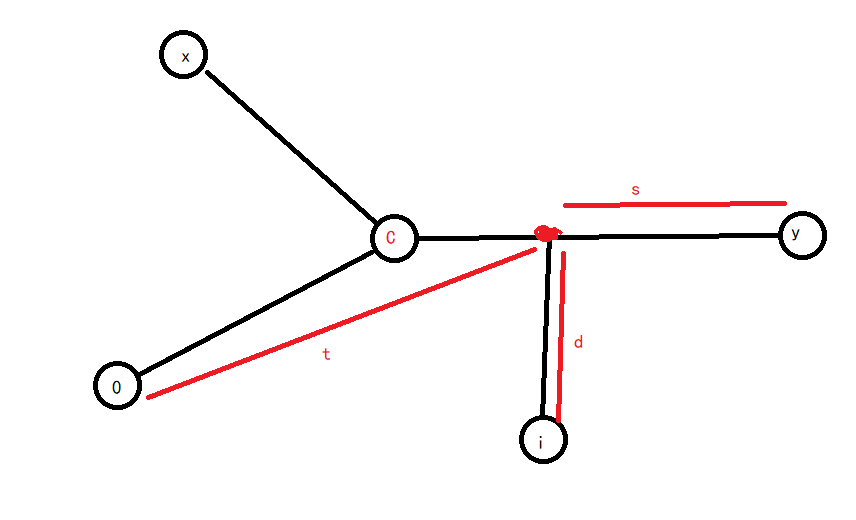
假设直径两端点为 \(x,y\) ,点 \(i\) 到 \(0\) 到 \(x\) 的路径的距离为 \(d\) ,然后设往这个点到直径上的点对应点 \(y\) 的距离为 \(s\) , 到 \(0\) 的距离为 \(t\)。
那么显然可以得到下列几个式子:
然后自己消元可以求解出 \(d\) 和 \(s\) 。
也就是
求直径时存下每个点距离端点的距离后这个可以直接解决。
然后我们知道这个直径点 \(C\) 在 \(x\to y\) 上,也在 \(0\to y\) 上,因为 \(0\) 往 \(y\) 走距离更大。
于是求出每个点的 \(s\), 与 \(dis(x,y)−s\) 之后取 \(\max\), 最后取 \(\min\) 就能得到半径 \(R\) 。
求出直径后,通过求出 \(x\) 到中点的距离,可以将 \(d\) 改为每个点到中点的距离,如果 \(dis(a,b)<d_a+d_b\) 那么这两个就是同一个子树,否则就不是。
那么我们知道这个方法后,我们可以通过判断两两是否在同一子树的方式来确定是否有一个子树的叶子多于 \(\dfrac{n}{2}\) ,问题就变成了查找这些数字重是否存在绝对众数。
摩尔投票可以求出第二问。
点击查看代码
XXI Open Cup GP of Korea – B
先考虑如何判断能否从 \((1,1)\) 到达 \((n,m)\)。下面给出了几种无法到达的情况:
存在一行被阻断,即 \(\min\{a_i\}+\max\{b_j\}<0\) 。
存在一列被阻断,即 \(\max\{a_i\}+\min\{b_j\}<0\) 。
起点被阻断,即存在 \(1\le x\le n,1\le y\le m\) 使得 \(a_x+b_j<0\pod{1\le j\le y}\) 且 \(a_i+b_y<0\pod{1\le i\le x}\) 。
终点被阻断,即存在 \(1\le x\le n,1\le y\le m\) 使得 \(a_x+b_j<0\pod{y\le j\le m}\) 且 \(a_i+b_y<0\pod{x\le i\le n}\) 。
事实上,这同时也是 \((1,1)\) 无法到达 \((n,m)\) 的必要条件 (即四个条件都不满足时一定能到达)。
证明 称 \(a_i+b_j\ge 0\) 的点 \((i,j)\) 为好点,其余点为坏点。条件 \(1\) 不满足意味着存在一列都是好点,不妨设为列 \(c\) 。条件 \(2\) 不满足意味着存在一列都是坏点,不妨设为行 \(r\)。只需证明 \((1,1)\) 能到达 \((r,c)\) 且 \((r,c)\) 能到达 \((n,m)\) 即可。由于过程类似,以 \((1,1)\) 到 \((r,c)\) 为例。 如果 \(r=1\) 或 \(c=1\) 则得证。否则,一定存在一行 \(r'<r\) 使得 \((r',j)\pod{1\le j\le c}\) 都是好点或存在一列 \(c'<c\) 使得 \((i,c')\pod{1\le i\le r}\) 都是好点 (否则可以发现条件 \(3\) 成立)。于是就转化到了 \(r+c\) 更小的情况,重复此过程直到 \(r=1\) 或 \(c=1\) 即可。
接下来考虑如何计算答案。条件 \(3,4\) 会直接去掉一些起点和终点。剩下的点中,条件 \(1,2\) 为每个起点限定了一个区间,且区间的两端点都是单调的,可以直接用指针维护。于是只需要解决条件 \(3,4\) 即可。
以条件 \(3\) 为例。枚举 \(x\),找到最小的 \(j\) 使得 \(a_x+b_j\ge 0\) (排序后用一个指针扫),那么只需要考虑所有小于 \(j\) 的 \(y\) 中 \(b_j\) 最小的一个。接着找到最大的 \(i<x\) 使得 \(a_i+b_y\le 0\) (单调栈 + 二分),那么从 \(i+1\) 到 \(x\) 的所有起点都不可能到达任何终点 (用差分记录即可)。
时间复杂度 \(O(n\log n+m)\) 。
点击查看代码