多校联训组合计数、概率期望专题
[AGC005D] ~K Perm Counting
正着不好求，那我直接容斥，用 \(f(i)\) 来表示钦定至少 \(i\) 个地方冲突的方案数。答案就是 \(\sum_{i=1}^n\limits (-1)^i \times f(i)\) 。
这种排列计数可以对应到这样的图上：
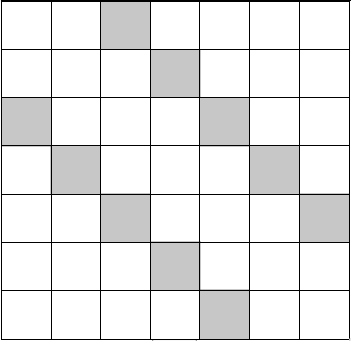
所求的排列个数，就等于在这样的棋盘格子内放 \(n\) 个互不攻击的車，且阴影格子不能放的方案数。上图是 \(n=7,k=2\) 的情况。
考虑现在的还有什么限制，发现同一行同一列的阴影格子还是不能同选。把不能同选的格子连上边：
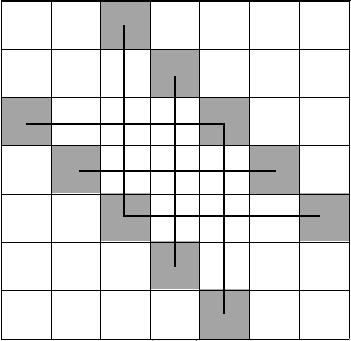
那 \(f_i\) 其实就是这个图大小为 \(i\) 的独立集个数。
很明显这个图就是若干条链，考虑把这些链连起来。转为求从这一排结点中选 \(i\) 个，拼接的位置可以相邻，其他位置不能相邻的方案数。于是它变为了一个简单的 \(\text{DP}\) 问题，\(O(n^2)\) 解决。
点击查看代码
[AGC026D] Histogram Coloring
考虑一个正方形的情况下怎么做，对于第 \(i\) 层向 \(i+1\) 层转移时，可以将第 \(i\) 层取反后放在第 \(i+1\) 层，同时，如果第 \(i\) 层是黑白相间的，也可以将第 \(i\) 层原封不动复制到第 \(i+1\) 层，容易发现，这是唯一的两种方式。
对于不是矩形的情况，可以利用一种类似于笛卡尔树上 \(\text{DP}\) 的方式，找到区间内的最小值，先递归处理最小值以上的部分，再合并即可，由于数据范围比较小，实际建树时可以暴力去做。
点击查看代码
【UNR #2】黎明前的巧克力
首先发现异或值相同那异或起来就是 \(0\) 。
那我们可以考虑这么一个东西，就是我们先求它们集合的并集，然后再把集合里面的元素分给它们，那对于大小为 \(x\) 的方案数就是 \(2^x\) 。
然后这个东西显然可以用 \(\text{FWT}\) 优化，就是每次乘上一个数组 \(f\)：在 \(0\) 的位置是 \(1\)，在 \(a_i\) 的位置是 \(2\) 。
我们发现每次乘上的东西很简单，考虑能不能从这里下手，然后我们会发现对于 \(\text{FWT}\) 之后的每一位，它要么是 \(−1\) 要么是 \(3\) ，重载运算符，统计出数量后统一处理即可。
点击查看代码
CF708E Student's Camp
对于每一行，先考虑算变成区间 \([l,r]\) 的概率。
设 \(k\) 天内，消失 \(i\) 个格子的概率为 $ g_i = {k\choose i} p^i \times (1-p)^{k-i}$ 。
所以剩下区间 \([l,r]\) 的概率为 \(g_{l-1} \times g_{m-r}\) 。
当然还需要检查这段区间长度是否合法，因为最多消失 \(2k\) 个格子。
转移式子不难写出。
复杂度 \(O(nm^4)\) ，显然不行，而且状态数都为 \(O(nm^2)\) 。
那考虑优化状态，去掉左端点的限制。
设 \(dp_{i,r}\) 表示第 \(i\) 行的剩余区间的右端点为 \(r\)，第 \(0\) 行到第 \(i\) 行都联通的概率，转移的时候枚举 \(l\) 进行转移。
它满足 \(r_1 \geq l, l_1 \leq r\) ，那么容斥把这一部分算出来即可。
对于 \(r_1 < l\) 的部分，枚举 \(l\) 时计算 \(\sum_{j=1}^{l-1} dp_{i-1,j}\) 。
对于 \(l_1 > r\) 的部分，因为网格是对称的，所以 \(f_{i,r}\) 也可以表示左端点为 \(m-r+1\) 且联通的概率，因此这一部分可以计算为 \(\sum_{j=1}^{m-r} f_{i-1,j}\) 。
于是转移如下。
考虑前缀和优化。
令 \(s_{j}\) 表示 \(\sum_{k=1}^j f_{i-1,k}\) 。
在令 \(p_i\) 和 \(q_i\) 依次为 \(g_i\) 与 \(g_i \times s_i\) 的前缀和，之后即可做到 \(O(1)\) 转移，总时间复杂度 \(O(nm)\) 。
点击查看代码
[ARC096C] Everything on It
考虑容斥，设 \(S(i)\) 表示有 \(i\) 个不合法的酱，其他的 \(n-i\) 个酱随意的方案数。那么首先令 \(f(i)\) 表示 \(i\) 种不合法的酱的方案数，有：
考虑将 \(i\) 个元素划分成 \(j\) 个集合，可能有元素不出现的方案数为 \(s[i][j]\) ，可以用一种类似斯特林数的方法预处理出来，那么有：
其中，计算 \(2^{2^{n-i}}\) 时可以使用欧拉定理，其余部分直接计算即可，时间复杂度 \(O(n^2)\) 。
点击查看代码
[AGC008E] Next or Nextnext
我们考虑最终的那个排列 \(p\)，建一个图，将点 \(i\) 向点 \(p_i\) 连边。因为这是个排列，所以每个点出度入度都为 \(1\) ，所以一定由若干环构成。
考虑其中的一个环，我们擦掉它的所有边，然后将 \(i\) 向 \(a_i\) 连边，可以知道 \(a_i\) 是它前面一个节点或者前面的前面一个节点。
有四种情况。
- 所有 \(i\) 的 \(a_i\) 都是它的前面一个节点，则环保持不变。
- 所有 \(i\) 的 \(a_i\) 都是它前面的前面的节点，且环为奇环，则环变成同构的另一个环
- 所有 \(i\) 的 \(a_i\) 都是它前面的前面的点，且原环为偶环，则这个环会被拆成两个相同大小的环。
- 有的是前面一个节点，有的又是前面的前面，则变成了一棵由一个环和若干指向环的链构成的基环内向树。
行吧，现在我们手头上只有由 \(a\) 构成的那张图，没有由 \(p\) 构成的那张图，所以我们就要反过来考虑了。
首先我们找到所有的环，先记录每个大小的环有多少个，那么每种大小可以单独考虑，\(\text{DP}\) 一下，决策就是这种大小的第 \(k\) 个环是和前面的环合并呢，还是单独组成 \(p\) 图中的环。最后用乘法原理乘起来这些东西。
对于一棵基环内向树，我们考虑相邻两个“脚”（即挂在环上的链），将“脚”往环里面塞，并且要求还是一条边与它指着的节点中间最多只能插一个节点。大致如下图：
这个脚可以塞到树里的位置，就是到下一个脚之间的边，假设这些边有 \(l_2\) 条，这个脚的长度为 \(l_1\) ，那么：
若 \(l_2<l_1\)，有 \(0\) 种方案。
若 \(l_2=l_1\)，有 \(1\) 种方案。
若 \(l_2>l_1\)，有 \(2\) 种方案。
可以用乘法原理搞，就做完了。
点击查看代码
【UNR #5】提问系统
令 \(p_r=x,p_b=n-x\) 答案变成 \(x(n-x)^2\)，也就是 \(x^3-2nx^2+n^2x\) 。
将入栈出栈操作转化成一棵树，那么 \(c_r,c_b\) 就转化为从根节点到每个点的路径上的颜色数限制，设 \(dp[x][i]\) 表示从根节点到 \(x\) 的路径上有 \(i\) 个 \(\text{R}\) 操作，子树内所有方案中 \(x\) 的 \(0-3\) 次方的和，最后将 \(dp[rt][0]\) 的 \(x^1,x^2,x^3\) 代入 \(x^3-2nx^2+n^2x\) 即可。
点击查看代码
[AGC009E] Eternal Average
考虑取平均数的过程会形成一个树形结构，叶子结点为初始的 \(0,1\)，每个非叶子结点都是 \(k\) 叉的，表示将其所有孩子合并为一个数。则深度为 \(i\) 的 \(1\) 对答案的贡献即为 \(\dfrac 1{k^i}\) ，且我们注意到最后的结果只和每层叶子中 \(1\) 的个数有关，而与 \(1\) 具体的摆放顺序无关。
记 \(d=\dfrac{n+m-1}{k-1}\) ，即该树的深度，不难注意到所有数都可化为 \(\dfrac{A}{k^d}\) 的形式（其中 \(A\) 为一个整数）。
直接枚举每一层的 \(1\) 的个数来统计会导致算重，因为某一层的 \(k\) 个 \(1\) 等价于上一层的 \(1\) 个 \(1\)，于是我们考虑枚举进行了 \(x\) 次把 \(k\) 个 \(1\) 变成了一个 \(1\) 的操作，那么我们会令新的 \(d'\gets d - x\)，\(M'\gets M - x(k - 1)\) 。
并且如果某一层有大于等于 \(k\) 个 \(1\)，那么我们可以把它们调整顺序（因为顺序不改变结果）后“合并”为一个 \(1\)，使得其在枚举 \(x+1\) 次把 \(k\) 个 \(1\) 变成了一个 \(1\) 的操作时再统计。
于是若要统计不重复，每一层都必须只有不超过 \(k - 1\) 个 \(1\)，不难发现此时最终的平均数 \(\dfrac A{k^d}\) 中的 \(A\) 满足：\(\dfrac Ak\)（因为第 \(0\) 层不可能有叶子结点，所以要除个 \(k\)）是一个 \(d'\) 位的 \(k\) 进制数，且每位数值之和恰为 \(M'\)（因为此时 \(1\) 的总数为 \(M'\)），不难验证该条件是充要的。
不难用一个朴素的背包 \(dp\) 做到 \(\mathcal O(n^2)\)（假设 \(n,m,k\) 同阶）的时间复杂度。
点击查看代码
[AGC013E] Placing Squares
矩阵乘法暴力维护即可。
点击查看代码
[AGC016E] Poor Turkeys
实际上可以无脑 2-SAT。
考虑枚举鸡 \((i,j)\) 是否能存活。
就是说我们要尽可能的保护 \(i\) 和 \(j\) 。
假设遇到了一个指令 \((p,i)\)，我们要杀的一定是 \(p\)。
当然 \(p\) 必须存在，换句话说就是要在这条指令前尽可能的保护 \(p\)。
倒着扫，同时维护一个数组 \(al\)，\(al_i\in\{0,1\}\)。
\(al_i\) 表示当前鸡 \(i\) 是否受到保护。
初值 \(al_x=al_y=1\) 。
扫到一个指令 \((p,q)\) 的时候，若 \(p\) 受到保护，则这一步要杀的就是 \(q\)，进而 \(q\) 在这一步前受到保护。\(q\) 同理。
然而若 \(p,q\) 均受到保护，则这一步必须要杀其一，进而鸡 \((i,j)\) 无法同时存活。
然而这样做是 \(O(n^2m)\) 的。
令人震惊的是，这个暴力已经可以通过本题，但我们可以通过改变循环顺序外加 \(\text{bitset}\) 优化做到 \(O(\dfrac {n^2m} w)\)
点击查看代码
[AGC018E] Sightseeing Plan
1. 一个点到一个点
从 \((x_1,y_1)\) 到 \((x_2,y_2)\) 的最短路径，就是只能往上或者往右走。
最短路径条数就是：\({x2-x1+y2-y1\choose x2-x1}\)
2. 一个点到一个矩形
\(F(x,y)\) 表示，从 \((0,0)\) 到 \((x,y)\) 的路径条数，这个可以直接算，发现 \(F(x,y)=\sum_{j=0}^yF(x-1,j)\) 。
可以理解为，从原点到所有的 \((x-1,j)\) 然后向上走一步，然后直接向右到达 \((x,y)\) ，肯定不重不漏。
那么，可以得到：
从 \((0,0)\) 到一个矩阵路径，就是 \(F(x2+1,y2+1)-F(x2+1,y1)-F(x1,y2+1)+F(x1,y1)\) ，只要计算四个点即可
3. 一个矩形到一个矩形
\(G\) 表示路径条数，\(M_1\) 代表第一个矩形，\(M_2\) 代表第二个矩形，要求的就是：
可以提出两个 \(\sum\)，变成枚举一个点，求到另外一个矩形的方案数。
其实就是：
\(xx,yy\) 代表那四个关键点。（省略了四个关键点正负号）
反过来，每个关键点都会被 \(M_1\) 所有的点统计一次。
所以，一个关键点的贡献，就是这个关键点到 \(M_1\) 的路径条数。
就是这个关键点到 \(M_1\) 的四个关键点路径条数。（当然，要有正负号）
所以，一个矩形到一个矩形的路径条数，就是两个矩形四个关键点分别进行条数计算。处理好符号即可。
4. 一个矩形经过一个矩形再到另一个矩形
可以把三的结论推广，第一个矩形四个关键点，到第三个矩形四个关键点，然后路径上经过第二个矩形的方案数。
所以，\(4\times 4\) 枚举第一第三个矩形的关键点的话，
问题就变成了从一个点出发，经过一个矩形再到另外一个点的方案数，直接枚举还是 \(O(n^2)\) 的。
发现，经过第二个矩形， 必然要么从 \((x,y_3)\)（下边界）要么从 \((x_3,y)\)（左边界） 进入。
我们枚举进入点，再乘上从进入点到终点的方案数就是这个进入点的贡献。
必然不重不漏地枚举完了所有的合法路径。
5. 一个矩形经过一个矩形中的一个点再到另一个矩形
我们经常转化研究对象，尝试分开统计贡献。
分开统计的前提是，贡献必须可以处理成互不相关的形式。
一条路径的选点方案数怎么计算？
进入点 \((x_1,y_1)\) ，离开点 \((x_2,y_2)\)，有 \(len=x_2-x_1+y_2-y_1\)，而 \(x_1,x_2,y_1,y_2\) 可以分离。
那么，我们可以枚举进入点。
贡献是：\((-1)\times\) 刚才的两个组合数 \(\times(x+y)\) 。
离开点：
贡献是：\((+1)\times\) 刚才的两个组合数 \(\times(x+y)\) 。
相加后，对于每个合法的路径，恰好被计算了两遍。（进入离开点各一次）
第一遍把 \(-x_1-y_1\) 算上，第二遍把 \(x_2+y_2\) 算上。
所以，每个合法路径贡献就是 \(len\) 次，符合题意。
点击查看代码
[AGC023E] Inversions
考虑总方案数是：
我们令 \(a_i\) 的排名为 \(b_i\)，\(c_i\) 为排好序后的 \(a_i\)，即：
考虑每两个位置的对于逆序对的贡献，不妨先设这两个位置为 \(i\) ，\(j\) 。
若 \(j<i\) 且 \(a_j<a_i\)，我们求其的逆序对贡献。
由于是逆序对，所以 \(a_i\) 比 \(a_j\) 大的部分可以省去，然后发现就是这样？
这个式子的组合意义实际上就是求出在 \(a_i\) 与 \(a_j\) 相同的时候的总方案数，然后除以 \(2\) ，就是 \(p_j>p_i\) 的方案数了。
若 \(i<j\) 且 \(a_i>a_j\) ，我们可以求其的顺序对贡献，用总的减去它。
发现对于前后的，只有一小部分不一样，我们考虑先来处理共同部分：
前面的这个东西对于每一个 \(i\) 都是一样的，后面的一半可以用线段树来维护，我们考虑从小到大往线段树中添加东西，对于当前位置 \(i\) ，令其排名为 \(k\) ，排名比其小的部分已经在线段树中了，我们考虑直接提取出区间和，然后对于全局进行一个区间乘 \(\frac{c_k-k}{c_k-k+1}\) ，同时将位置 \(i\) 的部分改为 \(a_i-b_i\) 就可以了。
点击查看代码
[AGC012F] Prefix Median
首先我们可以发现一个很显然的性质，\(b_n\) 是确定的，等于 \(a\) 的中位数。
为了方便讨论，我们先将排个序。
由此，我们继续讨论 \(b_{n-1}\) 的情况，相较于 \(b_n\) ，我们发现我们需要在所有的 \(n\) 中删去两个数，可能是在 \(b_n\) 的左右或是它自己，无论如何我们都可以发现，他们在 \(a\) 中的位置不会超过 \(1\)。
推广得到，\(b_i\) 不会与 \(b_{i+1}\) 在 \(a\) 中的位置超过 \(1\)。
所以我们可以得到两个性质：
性质1：对于任意 \(i < j\) 不会 存在 \(b_j < b_i < b_{j+1}\) 或者 \(b_{j+1} < b_i < b_{j + 1}\)
性质2：\(a_i \leq b_i \leq a_{2 \times n - i}\)
所以对于一个 \(b_i\) 的取值范围很显然就是 \([a_i , \min(b_j)]\) 和 \([\max(b_j) , a_{2 \times n - i}]\) 。
所以我们定义 \(dp[i][L][R]\) 表示确定 \(b_i\) 后，在上述 \(1\) 号区间有 \(L\) 个取法，\(2\) 号区间 \(R\) 种取法的方案数。
\(dp\) 就很好转移了，我们只需要暴力枚举一组 \(dp_{i+1,l,r}\) ，然后暴力枚举我们钦定的 \(b_i\) ，同时确定钦定的 \(b_i\) 的\(L\) 和 \(R\) 就可以了。
Gym 103415D Unnamed Easy Problem
[AGC020F] Arcs on a Circle
首先断环为链, 以最长的弧的起点作为链的起点(同时也是链的终点), 由于将环的的问题转化为了线段的问题, 下面将弧描述为线段.
然后由于坐标的连续性为求解带来的困难, 我们需要将坐标离散化, 套路化的方法是将坐标 \(x\) 分为整数部分 \(a\) 和小数部分 \(b\) , 对小数部分进行离散化。
离散化之后, 坐标变为 \(nc\) 个, 这个问题就可以比较容易的解决了。 \(\mathcal O(n!)\) 地枚举各个线段小数部分的相对大小, 然后状压 \(\text{DP}\) 一下就好了。
点击查看代码
