关于路径计数问题
记号与定义
以下定义都是基于每次只能往右上或左下走这一条件的。
也就是说:当你处于 \((x,y)\) 时,你只能走到 \((x+1,y+1)\) 或 \((x+1,y-1)\)。
我们认为一条路径与一条直线的相交次数就是有多少个整点既在路径上又在直线上。
一条路径与一条直线的不相交就是相交次数为 \(0\),反过来相交就是相交次数不为 \(0\)。
组合数 \(\dbinom{n}{m}=C_n^m\),也就是在 \(n\) 个物品中挑选 \(m\) 个的方案数。
记号 \([a,b,c,d]\) 就是从 \((a,b)\) 走到 \((c,d)\) 的路径数。
记号 \(<a,b,c,d,k>\) 就是从 \((a,b)\) 走到 \((c,d)\) 且与直线 \(y=k\) 相交的路径数。
记号 \(\{a,b,c,d,k\}\) 就是从 \((a,b)\) 走到 \((c,d)\) 且与直线 \(y=k\) 不相交的路径数。
记号 \([a,b,k]\) 就是从 \((0,0)\) 走到 \((a,b)\) 的所有路径与直线 \(y=k\) 相交次数之和。
记号 \(\left| a,b,k_1,k_2 \right|\) 就是从 \((0,0)\) 走到 \((a,b)\) 且与直线 \(y=k_1\) 和 \(y=k_2\) 都不相交的路径数。
记号 \(\left\langle\ a,b,k_1,k_2 \right\rangle\) 就是从 \((0,0)\) 走到 \((a,b)\) 且与直线 \(y=k_1\) 相交而与直线 \(y=k_2\) 不相交的路径数。
无限制下的路径条数
定义一条合法路径,只要它满足以下两条即可:
从 \((a,b)\) 出发到 \((c,d)\) 停下。
当你处于 \((x,y)\) 时,你只能走到 \((x+1,y+1)\) 或 \((x+1,y-1)\)。
那么合法路径条数为 \(\dbinom{c-a}{\frac{c-a+d-b}{2}}\) 。
记为 \([a,b,c,d]\) ,也就是说 \([a,b,c,d]=\dbinom{c-a}{\frac{c-a+d-b}{2}}\) 。
证明
考虑有 \(x\) 步是往右上走,有 \(y\) 步是往右下走。
那么 \( \begin{cases}x+y=c-a\\b+x-y=d\end{cases} \) ,解得 \(\begin{cases}x=\dfrac{c-a+d-b}{2}\\y=\dfrac{c-a+b-d}{2}\end{cases}\) 。
考虑到总共 \(c−a\) 步,其中放入 \(x\) 个往右上走的,方案数就是 \(\dbinom{c-a}{\frac{c-a+d-b}{2}}\) 。
有一条不可碰横线的计数
定义一条合法路径,它要满足以下几条:
从 \((a,b)\) 出发到 \((c,d)\) 停下。
当你处于 \((x,y)\) 时,你只能走到 \((x+1,y+1)\) 或 \((x+1,y−1)\) 。
路径与直线 \(y=k(k<b\) 且 \(k<d)\) 不能有任何交点。
那么合法路径条数为 \([a,b,c,d]-[a,b,c,2k-d]\) 。
记为 \(\{a,b,c,d,k\}\) ,也就是 \(\{a,b,c,d,k\}=[a,b,c,d]-[a,b,c,2k-d]\) 。
当然为了方便,我们再记从 \((a,b)\) 到 \((c,d)\) 且必须经过直线 \(y=k\) 的路径数为 \(<a,b,c,d,k>\) 。
那么会有 \(<a,b,c,d,k>=[a,b,c,2k−d]\) 。
证明
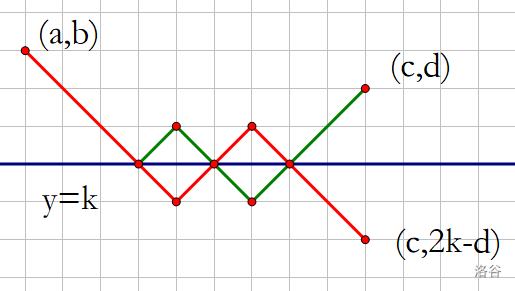
如图,把 \((c,d)\) 关于 \(y=k\) 对称到 \((c,2k-d)\) 。
那么考虑所有从 \((a,b)\) 到 \((c,2k-d)\) 的路线,可以发现一定与 \(y=k\) 有交点,取第一个交点出来,把之后的路线关于 \(y=k\) 对称一下就是到 \((c,d)\) 的一个与 \(y=k\) 相交的路线(就是红线变绿线)。
容易发现这就是 \(<a,b,c,d,k>\) 。
当然更严谨的证明还要说所有与 \(y=k\) 相交的路径也能对应一条从 \((a,b)\) 到 \((c,2k-d)\) 的路径,从双射的角度证明他们是等价的。
所以 \(<a,b,c,d,k>=[a,b,c,2k-d]\) 。
然后就很好得知 \(\{a,b,c,d,k\}=[a,b,c,d]-[a,b,c,2k-d]\) 了。
与一条直线的相交次数之和
定义一条合法路径,它要满足以下几条:
从 \((0,0)\) 出发到 \((a,b)\) 停下,其中 \(a,b\) 为正整数。
当你处于 \((x,y)\) 时,你只能走到 \((x+1,y+1)\) 或 \((x+1,y-1)\) 。
(为了方便,起始点就定为了 \((0,0)\) ,其他情况都可以等同过来。)
定义一条合法路径的权值为其与直线 \(y=k\) 相交的次数。
求所有合法路径的权值之和。
求解
那么这里开始可能就要顺着我的思路来讲了(毕竟之前都是些熟知的东西)。
首先把答案也用一个符号记录 \([a,b,k]\) 。(这个要跟1.中的 \([a,b,c,d]\) 区分一下)
然后上图。
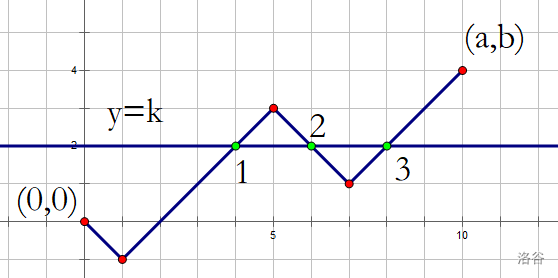
如图要计算绿点的数量。
那么这看起来不是一个简单的组合数能表示的。
所以我们考虑缩小问题规模。
怎么做呢?
先计算最后一个绿点的出现次数。
其实就是路径条数,就是 \(res1=[0,0,a,b]\) 。
然后计算不是最后一个的绿点的出现次数。
也就是在这个点 \((i,k)\) 之后再与直线 \(y=k\) 有交点。
式子:\(\begin{aligned}res2=\sum\limits_{i=0}^{a-1}[0,0,i,k]\times (<i+1,k+1,a,b,k>+<i+1,k-1,a,b,k>)\end{aligned}\)
为什么后面是一个奇怪的和呢?
还记不记得 \(<a,b,c,d,k>\) 计算的是与 \(y=k\) 有交点的路径数?
那么就是说直接 \(<i,k,a,b,k>\) 并不是“在这个点之后再与直线 \(y=k\) 有交点”的方案数。
所以要先从 \((i,k)\) 走一步再求。
于是就列出了上面那个式子,然后继续化。
第一步是因为把 \(2.\) 中的结论代入,可以发现这个加和的其实是一个东西,直接乘 \(2\) 就好了;
第二步就是十分简单的把先从 \((i,k)\) 往前走一步换个方向考虑,改为先从 \((a,b)\) 往回走一步,这样就是上面这个东西了。
接着我们可以发现 \(res2=2\times[a-1,b+1,k]\)
为什么呢?
让我们看到求 \([a,b,k]\) 第二种想法。

还是上面那图。
我们想,不去缩小规模,可以直接枚举每个绿点会出现在多少条路径中。
式子:\([a,b,k]=\sum\limits_{i=0}^a[0,0,i,k]\times[i,k,a,b]\)
意思十分的简单,从 \((0,0)\) 到 \((i,k)\) 再到 \((a,b)\),就是经过 \((i,k)\) 的所有路径了。
然后我们看到 \(\begin{aligned}res2=\sum\limits_{i=0}^a[0,0,i,k]\times [i,k,a-1,b+1]\times 2\end{aligned}\) 这是不是十分的像?
所以观察一下,我们就可以得到 \(res2=2\times[a-1,b+1,k]\)
结合 \(res1=[0,0,a,b]res1=[0,0,a,b]\),可得 \([a,b,k]=res1+res2=[0,0,a,b]+2\times[a-1,b+1,k]\)
这样就可以缩小问题规模了!
为什么呢?
\([a,b,k]=[0,0,a,b]+2\times[a-1,b+1,k]\)
看到 \([a-1,b+1,k]\) ,它可以用上面的式子递归的去分解!
边界?
可以发现当 \(a<b\) 时,甚至无法走到 \((a,b)\),所以 \([a,b,k]\) 为零,以这个为边界即可。
然后只要不停分解就好了,可以得到一个十分完美的式子:
我们发现居然跟 \(k\) 无关!
其实这是因为我们保证了 \(y=k\) 处于两个点的纵坐标之间,而当 \(y=k\) 不在这两个点的纵坐标之间呢?
我们可以发现一个十分重要的事情,就是 \(res1\) 和 \(res2\) 不一样了!
具体个怎么不一样呢?
最后一个绿点的出现次数 \(res1\) 原本是直接走到 \((a,b)\) 就好了,因为一定会碰到直线 \(y=k\) ,但是现在就不一样了。
事实上现在应有 \(res1=<0,0,a,b,k>=[0,0,a,2k-b]\) 。
同理的 \(res2\) 也会有点不一样,读者自己推一下可以发现 \(res2=2\times [a-1,b-1,k]\) 。
这样 \(k\) 就会在式子中,最终会有:
其实直接考虑把 \((a,b)\) 关于 \(y=k\) 对称到 \((a,2k-b)\) 也能得到一样的式子。


