万能欧几里得算法
基本模型
很多类欧几里得问题都可以归结为以下这个模型：
考虑笛卡尔坐标系中一条直线 \(y=\dfrac{px+r}{q}\) ，并画出所有形如 \(x=k\ (k\in Z)\) 的竖线以及 \(y=h\ (h\in Z)\) 的横线。
假想从左往右扫描这条直线，每遇到这条直线与一个横线的交点，则执行 \(U\) 操作
每遇到这条直线与一个竖线的交点，则执行 \(R\) 操作，规定同时遇到一条横线和竖线（即到达一个整点）时先执行 \(U\) 后执行 \(R\)。
这样一来，我们可以将一条直线转译成一个由 \(U,RU,R\) 组成的操作序列。
例如，考虑 \(y=\dfrac{3x+2}{5}\) ，其图像如下：
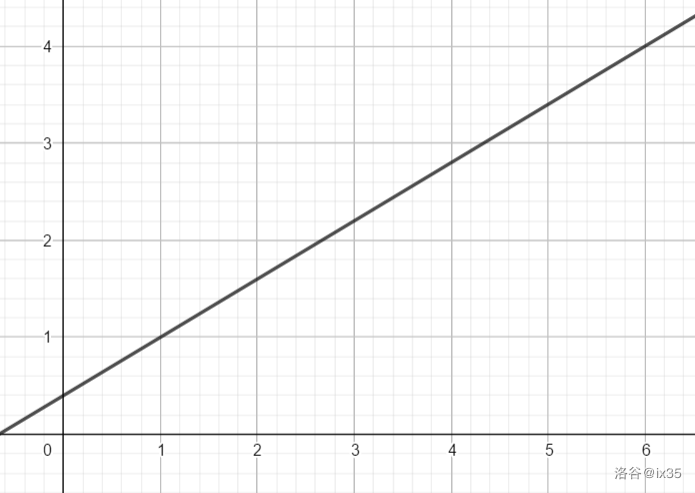
在 \(x\in (0,6]\) 的范围内，其对应的操作序列就是：\(URRURRURUR\)。
同时，操作要满足可合并性。例如上面的操作序列，我们设 \(P=UR\)，可以进一步转化为 \(PRPRPP\)。
操作的内容可能是对于一些变量做修改，具体的情况我们最后再说。而万能欧几里得的套路可以帮我们快速计算进行这样的操作序列后的某些信息。
我们将两个操作序列 \(S\) 和 \(T\) 的合并序列称为 \(S+T\) 或 \(ST\)，这个合并过程不一定满足交换律。
套路
解决问题的过程是递归的，我们设 \(solve(p,q,r,l,a,b)\) 表示处理 \(y=\dfrac{px+r}{q}\ (x\in (0,l])\) 这个线段，\(a,b\) 分别为遇到横线和竖线后执行的操作序列。
既然这个东西叫万能欧几里得，自然就和欧几里得算法的迭代有关，这分为两个部分。
第一部分：\(p\ge q\) 时，我们尝试将这个问题分解成规模为 \(p\bmod q\) 的子问题。
我们发现，如果 \(p\ge q\)，那么只要令 \(b'=a^{\lfloor \frac{p}{q}\rfloor}b\)，然后直接递归 \(solve(p\bmod q,q,r,l,a,b')\) 即可，这是因为每一个 \(b\) 的前面必然有至少 \(\lfloor \frac{p}{q}\rfloor\) 个连续的 \(a\)，它们可以和这个 \(b\) 合到一起。
第二部分：\(p<q\) 时，交换 \(p,q\) 地位，再进入第一部分的迭代。
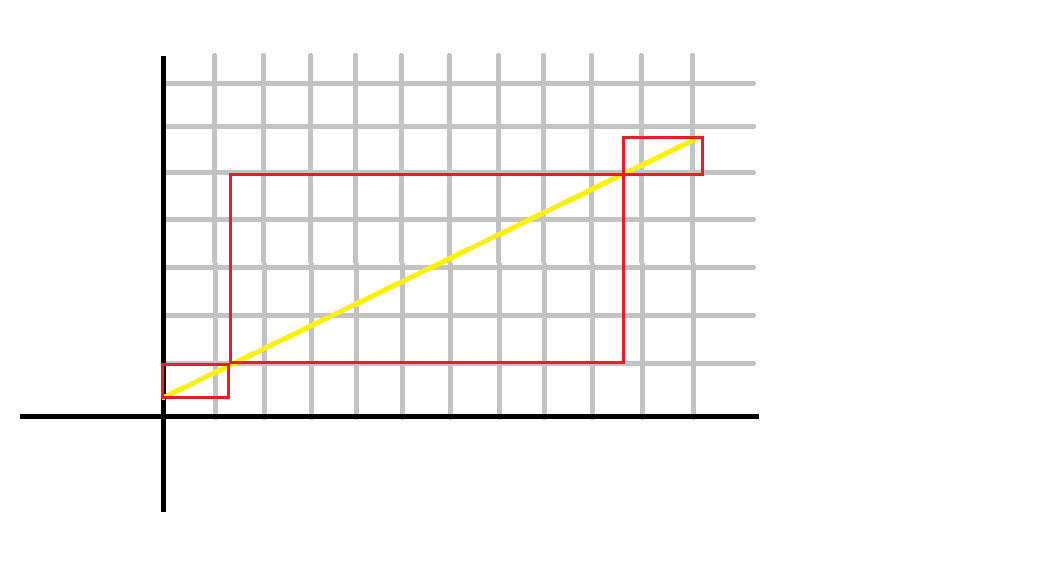
考虑将图像分成三部分，对于第一部分，可以求出与第二部分的分界点 \((x,1)\) ：
可知从 \(y\) 轴到第一个分界点一共有 \(\lfloor \dfrac{q-r}{p}\rfloor\) 个 \(b\) 操作，但是当分界点取到整点时，一二部分之间的 \(a\) 操作应该在第 \(\lfloor \dfrac{q-r}{p}\rfloor\) 个 \(b\) 操作后面，为了解决这个问题，我们将直线向左平移 \(\dfrac 1 p\) 个单位长度即可。
因此第一部分的贡献为：\(b^{\lfloor \frac{q-r-1\ \ \ \ }{p} \rfloor}\)，第一二部分的分界点贡献为一个 \(a\)。
接下来求出第二部分与第三部分的分界点 \((x,y)\)。
对于第二部分可以直接递归，为： \(solve(q,p,(q-r-1)\text{%}\ p,y-1,b,a)\) 。
同时，可以发现，第三部分贡献为 \(b^{l-x}\) ，记 \(m=\lfloor\dfrac{pl+r}{q}\rfloor,cnt=l-\lfloor \dfrac{qm-r-1}{p}\rfloor\)，有递归式：
例题
[BJOI2012]算不出的等式
观察性质题，但是可以用万欧板子直接过。
我们只需要讨论这题中 \(U\) 和 \(R\) 分别是什么，即可套用上面的做法。
首先考虑每个状态维护的值，我们设 \(s=\dfrac{x+r}{q}\) ，求 \(s\) 的和。
一般这样的题目中，还需要额外维护的是这一段操作序列中 \(U\) 和 \(R\) 的个数。
考虑合并状态 \(S,T\)，变为 \(W=S+T\) ：
显然 \(\text{W.cntu=S.cntu+T.cntu，W.cntr=S.cntr+T.cntr}\) 。
因为 \(T\) 中每次加的 \(y\) 都比原来增大了 \(\text{S.cntu}\)，因此，有：\(\text{W.sums = S.sums + T.sums + S.cntu × T.cntr}\) ，剩余部分套板子即可。
点击查看代码
【模板】类欧几里得算法
我们要求的是 \(s\) 的和，\(s\) 的平方和以及 \(s\times x\) 的和。
此外，为了计算 \(s\times x\) 的和，我们还需要记录 \(x\) 的和。
因此我们记录六个量：\(U\) 的个数 \(\text{cntu}\)，\(R\) 的个数 \(\text{cntr}\)，\(x\) 的和 \(\text{sumi}\)，\(s\) 的和 \(\text{sums}\)，\(s\) 的平方和 \(\text{sqrs}\)，\(s\times x\) 的和 \(\text{prod}\) 。
遇到 \(U\) 时，我们需要执行：\(\text{cntu ← cntu+1}\)
遇到 \(R\) 时，我们需要执行：\(
\text{cntr ← cntr+1}\\
\text{sumi ← sumi + cntr}\\
\text{sums ← sums + cntu}\\
\text{sqrs ← sqrs + cntr × cntr}\\
\text{prod ← prod + cntr × cntu}\\
\)
不难推出初始状态：\(U\) 的状态只有 \(cntu=1\)，\(R\) 的状态有 \(cntr,sums,sqrs\) 都为 \(1\)。
考虑合并状态 \(S,T\)，变为 \(W=S+T\) ：
因为 \(T\) 中每次加的 \(x\) 都比原来增大了 \(\text{S.cntr}\)，因此，有：\(\text{W.sumi = S.sumi + T.sumi + S.cntr × T.cntr}\) 。
将 \(\text{(s + S.cntu)}^2\) 展开，可得：\(\text{W.sqrs = S.sqrs + T.sqrs + T.cntr × S.cntu^2 + 2 × S.cntu × T.sums}\) 。
将 \(\text{(s + S.cntu)(x + S.cntr)}\) 展开，可得：\(\text{W.prod = S.prod + T.prod + S.cntu × S.cntr × T.cntr + S.cntu × T.sumi + S.cntr × T.sums}\) 。
最后，由于之前的讨论是基于 \(x\in (0,L]\)，本题 \(x\in [0,L]\)，所以最后 \(sums\) 上要加一个 \(\frac{R}{Q}\) ，而 \(sqrs\) 上要加一个 \(\frac{R^2}{Q^2}\) 。
点击查看代码
