组合游戏和博弈论
Nim游戏和SG值
给定一个有向无环图和一个起始顶点上的一枚棋子,Alice和Bob交替的将这枚棋子沿有向边进行移动,无法移动者判负。问是否有必胜策略。
首先定义 \(\text{mex}\) 运算,这是施加于一个集合的运算,表示最小的不属于这个集合的非负整数。例如 \(\text{mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0}\)。
对于一个给定的有向无环图,定义关于图的每个顶点的 \(\text{SG}\) 函数 \(\text{sg}\) 如下:\(\text{sg(x)=mex{ sg(y) | y是x的后继 }}\)。也就是说,一个点的 \(\text{SG}\) 函数为在它所有后继中都未出现的最小的值。
通过 \(\text{sg}\) 函数,我们可以把所有 \(\text{ICG}\) 游戏转换成 \(\text{Nim}\) 游戏,后手必胜当且仅当 \(\text{sg}\) 的异或和为 \(\text{0}\) 。
过程
1. 把原游戏分解成多个独立的子游戏,则原游戏的SG函数值是它的所有子游戏的SG函数值的异或。
即:
2. 分别考虑没一个子游戏,计算其 \(\text{SG}\) 值。
\(\text{SG}\) 值的计算方法:(重点)
-
可选步数为 \(1\) ~ \(\text{m}\) 的连续整数,直接取模即可,\(\text{SG(x)=x%(m+1)}\);
-
可选步数为任意步,\(\text{SG(x) = x}\);
-
可选步数为一系列不连续的数,用模板计算。
Moore’s Nimk
类似 \(\text{Nim}\),但是每次操作可以从任意选 \(1\) ~ \(\text{k}\) 堆石子并对于每一堆取任意量的石子,而不是只能取 \(1\) 堆。
做法:
从 \(\text{Nim}\) 中类推一下,\(\text{Nim}\) 是二进制异或和,这个就先把石子个数转为二进制,再对每一位做 \(\text{k+1}\) 进制异或和,也就是对每一位求 \(\text{sum % (k+1)}\) ,如果求出来每一位都为 \(0\),则先手必败,否则先手必胜。
证明:
对于一个 \(k-Nim\) 和等于 \(0\) 的状态,其进行一步操作后受到改变的最高位一定不会变回 \(0\),而对于 \(k-Nim\) 和大于 \(0\) 的状态你一定可以通过一次操作把它变成 \(0\)。
Nim积
引入:
在一个 \(n\) 行 \(m\) 列的表格里,每个格子里有一个硬币,有的正面朝上,有的反面朝上。
两人轮流操作,每次可以反转同一行或同一列的两个硬币,要求横坐标或纵坐标大的那个硬币必须是正面朝上的,令对手不能操作即为胜利。
可以发现,对于一个点 \((x,y)\) ,它的 \(\text{SG}\) 函数为 \(SG(x,y)=x⊕y\),因为每个棋子可以看作 \(Nim\) 游戏中的两堆大小分别为 \(x、y\) 的石子。
考虑第二个问题,假设每次可以反转的是一个矩形的四个顶点,要求横纵坐标都最大的那个硬币必须是正面朝上。
可以列出它的 \(\text{SG}\) 函数:
定义 \(Nim\) 积:
可以得到一些运算性质:
\(\text{(1)}\) 交换律:\(x \times y = y \times x\)
\(\text{(2)}\) 结合律:\(( x \times y ) \times z = x \times ( y \times z )\)
\(\text{(3)}\) 对异或的分配律:\(( x ⊕ y ) \times z = ( x \times z ) ⊕ ( y \times z )\)
\(\text{(4)}\) 单位元:\(x \times 1 = 1 \times x\)
费马数的一些运算性质
经过数学家的艰苦卓绝的努力,我们有两个十分强大的运算法则。
定义 \(\text{Fermat 2-power}\) 为 \(2^{2^n}\) ,其中 \(n∈N\) ,设其为 \(a\) 。
一个 \(\text{Fermat 2-power}\) 与任意小于它的数的 \(Nim\) 积为一般意义下乘法的积,即 \(a \times x=a\cdot x\ (x<a)\) 。
一个 \(\text{Fermat 2-power}\) 与自己的 \(Nim\) 积为自己的 \(\frac 3 2\) 倍,即 \(a \times a=\frac 3 2a=a⊕\frac a 2\) 。
有了这两条规律,结合上述的基本性质,我们可以得到一个单次 \(O(log^2n)\) 复杂度的分治算法:
计算 \(x \times y\) ,设 \(x=xa⋅P+xb,y=ya⋅P+yb\) ,其中 \(P\) 是一个尽量将 \(x,y\) 分为相同两半的费马数.
那么有
观察发现,对于其中 \((xa⊗yb)⊕(xb⊗ya)\) ,有:
更清楚地,我们令 \(a=xb × yb\)、\(b=(xa × yb)⊕(xb × ya)\)、\(c=xa × ya\) 。
而 \(P × P=\frac 3 2 \cdot P=P⊕\frac P 2\) ,进而有:
递归计算即可,时间复杂度 \(O(4^{\log \log n})\),即 \(O(\log^2 n)\):
ull Nim[257][257];
ull f(ull x,ull y,int len=32){
if(x<=1||y<=1)return x*y;
if(len<8&&Nim[x][y])return Nim[x][y];
ull ax=(x>>len),bx=(x^(ax<<len)),ay=(y>>len),by=(y^(ay<<len));
ull a=f(bx,by,len>>1),b=f(ax^bx,ay^by,len>>1),c=f(ax,ay,len>>1),d=f(c,1<<(len-1),len>>1);
ull res=((a^b)<<len)^a^d;
if(len<8)Nim[x][y]=res;
return res;
}
例题:
【GDOI2020模拟01.16】划愤
考虑 \(n=2\) 的情况,其实和 \(Nim\) 积的式子是一样的。
对于 \(n\) 比较大的情况,也就是把所有的单点 \(\text{sg}\) 值乘在一起。
发现原问题要求的就是矩阵和积式。
和积式没有多项式时间算法,但异或意义下加法与减法没有区别。
所以只要求行列式就好了。
然后为了能够进行高斯消元,需要处理逆元。
做法大概是,找到任意一个大于 \(y\) 的 \(2^{2^x}\),那么 \(y−1=y^{2^{2^x}−2}\)。
大概的理解就是,这个玩意在\(\mod 2^{2^x}\) 意义下是封闭的,所以满足费马小定理的样子。
点击查看代码
威佐夫博弈
有 \(2\) 个石子堆,两人轮流从一个石子堆中取任意数量的石子或同时从两个石子堆中取等量的石子。不能操作者输。
后手必胜当且仅当第一个数是两数差值乘黄金比下取整。
阶梯Nim
偶数台阶上的石子 \(\text{SG}\) 函数均为 \(0\),奇数台阶的 \(\text{SG}\) 函数为该台阶上的石子数量。
无向图删边游戏
树上删边游戏
在某一棵树上删除一条边,同时删去所有在删除后不再与根相连的部分。
双方轮流操作,无法再进行删除者判定为失败。
一个游戏中有多棵树,我们把它们的根都放在地板上,方便之后的处理。
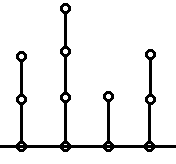
为了方便 我们先引入竹子(也就是链)
这部分就是 \(Nim\) 游戏的变形,有 \(\text{SG[x]=x}\)
克朗原理
对于树上每一个点,它的分支可以转化为以这个点为根的一个竹子。
竹子长度就是它各个分支的边的数量的异或和。
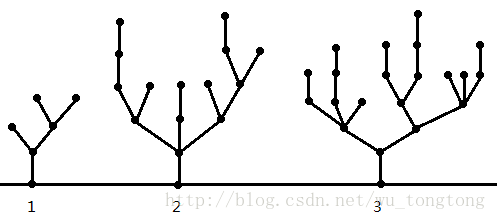
\(1\) 号树 最后是一条边的竹子 \(\text{SG}_1=1\)
\(2\) 号树 \(\text{SG}_2=8\)
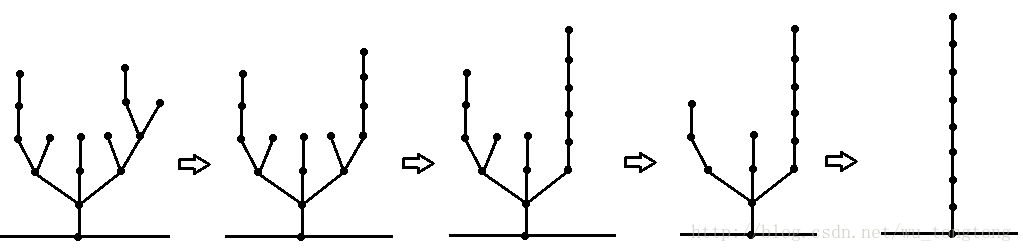
\(3\) 号树 \(\text{SG}_3=4\)

克朗定理的相关证明 【我是证明】
无向图上删边游戏
这里有一个无向图
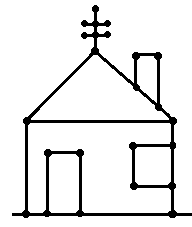
这里根等同于地板
费森定理
环上的点是可以融合的 并且不改变图的 \(\text{SG}\) 值。
以上图为例,门独立于大框,从门开始。
地板上的两个点可以视为一个 因为地板本身就是一个大点。
这样的话这扇门就成为了一个三角形 (也就是一个有三个点的环)。
费森原理指出,我们可以把换上一个点等价成一个自环,而这个环又可以成为一条边。

一般来讲
一个带奇数边的环就是一个只有一个端点的边
一个带偶数边的环就是一个点
那么这样的话就可以缩点了
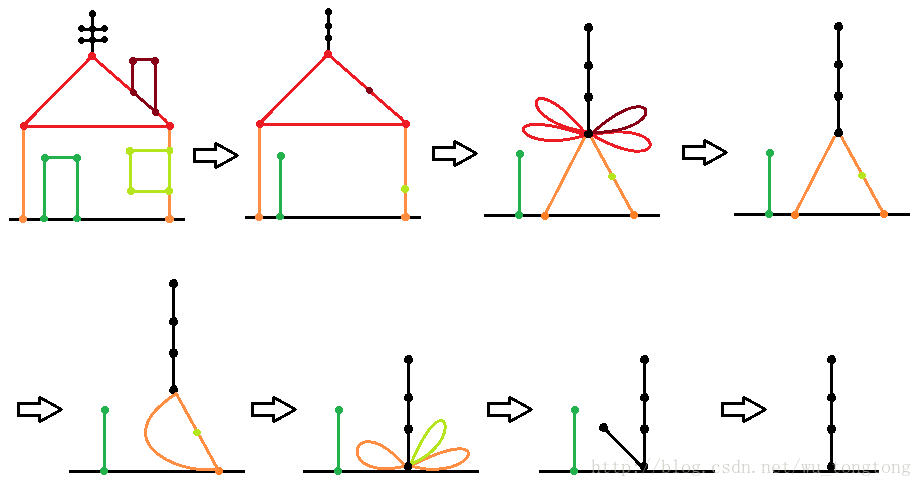
结论
对于无向图,我们先利用费森原理,将其转化为一棵树。
然后,对于一棵树,树上节点的 \(\text{SG}\) 值就是它的所有子节点的 \(\text{SG}\) 值 \(+1\) 之后的异或和。
例题
CF1149E Election Promises
发现图是一张 \(\text{DAG}\),定义一个节点的高度为它可以到达的节点的高度的 \(\text{mex}\),对每个高度计算 \(\text {SG}\) 函数异或和。
发现对于一个高度为 \(i\) 的集合,通过一次操作让高度小于 \(i\) 的集合异或和全变为 \(0\) ,而 \(i\) 集合本身的异或和要么从 \(0\) 变为非 \(0\),要么从非 \(0\) 变为 \(0\) 。
因此在所有集合的异或和均为 \(0\) 的情况下,无论先手如何操作,后手都可以通过一次操作保持所有集合的异或和均为 \(0\) ,先手必败。
对于存在至少一个集合的异或和不为 \(0\) 的情况,先手可以通过操作异或和不为 \(0\) 且编号最大的集合,使得所有集合的异或和均变为为 \(0\) ,此时先手必胜。
点击查看代码
[AGC016F] Games on DAG
补集转化,转为求 \(2^m\) 减去先手必败的方案数。
先手必败即为 \(1\)、\(2\) 号点 \(\text{SG}\) 函数相等,考虑状压 \(dp\),枚举每个集合中 \(\text{SG}\) 函数为 \(0\) 的点,强制其它点向这些点连边,统计方案即可。
点击查看代码


