杨氏矩阵与钩子定理
定义:
在数学中,杨表 \(\text{(Young table})\) 又称杨氏矩阵,最初用于对称群的表示理论。
杨图由有限个相邻的方格排列而成,其中,各横行的左边对齐,长度从上到下递增。分为英式画法和法式画法,这里只讨论标准杨表。
标准杨表:在杨图的 \(n\) 个方格中任意填入 \(1\) 到 \(n\) 中的相异正整数,各行和各列中的数字皆严格递增。

勾长、臂长、腿长
“臂长”是正右方的方格数,“腿长”是正下方的方格数,“勾长”是“臂长+腿长+1”
勾长公式
给定一个杨表 \(π_λ\) ,一共有 $n4 个方格。那么把 \(1\) 到 \(n\) 这 \(n\) 个数字填到这个杨表中,使得每行从左到右都是递增的,每列从下到上也是递增的(法式画法)。用 \(dim_{π_λ}\) 表示这样的方法个数。
勾长公式就是方法个数等于 \(n!\) 除以所有方格的勾长的乘积。
例如,对于拆分10=5+4+1的杨表,
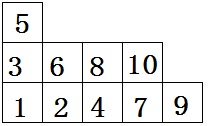
n个方格的标准杨表个数:
递推形式为:
等于 \(n\) 个点完全图的匹配方案数。
例如,\(n=3\) 时
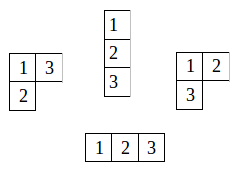
例子
问题: 1-16十六个数字分别填入十六格方框内,要求从左至右的数字是从小到大排列,从上至下的数字也是从小到大排列,问:有多少种排列方式。
分析:
这实际上一个是杨氏矩阵问题。
直接使用勾子公式,
按照 \(4*4\) 矩阵的形状,反对角线上的格子的钩子长度是一样的,

所以最终答案是:
三格骨牌 (trominoes)
考虑轮廓线 \(dp\) ,令 \(0\) 表示横向边界,\(1\) 表示纵向边界。
对于第一种骨牌,合法转移方案有两种:
对于第二种骨牌,合法转移方案有两种:
发现这四种操作可以归为一种,即将一个形如 \(0xx1\) 的段变为 \(1xx0\) 。
我们要求将 \(0...01...1\) 变为 \(1...10...0\) 的方案数,我们可以将坐标对 \(3\) 取模,分开处理。
问题转化为对三个 \(\frac{n}{3}\times \frac{m}{3}\) 的矩阵用小方格填满的方案数,转化为杨氏矩阵问题。
我们可以考虑将三个杨表放在一起,算钩长时只在一个表里算,有:
严谨证明可以考虑将三个操作序列合并:
令 \(\frac{n*m}{9}=k\),有:
可以得到相同的结论。
点击查看代码
标准杨表的插入算法
排列的性质可以由杨表直观地表现出来。RSK 插入算法 就提供了一个将杨表和排列联系起来的途径。它由 \(\text{Robinson}\), \(\text{Schensted}\) 和 \(\text{Knuth}\) 提出。
令 \(S\) 是一个杨表,定义 \(x->S\) 表示将 从第一行插入杨表中,具体如下:
-
在当前行中找到最小的比 \(x\) 大的数 \(y\)。
-
如果找到了,用 \(x\) 去替换 \(y\),移到下一行,令 \(y->x\) 重复操作 \(1\)。
-
如果找不到,就把 \(x\) 放在该行末尾并退出。记 \(x\) 在第 \(s\) 行第 \(t\) 列,\((s,t)\) 必定是一个边角。一个格子 \((s,t)\) 是边角当且仅当 \((s+1,t)\) 和 \((s,t+1)\) 都不存在格子。
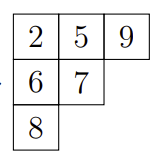
例如,将 \(3\) 插入杨表 \( \left [\begin{matrix} {2}&{5}&{9}\\ {6}&{7}&{ }\\ {8}&{ }&{ }\\ \end{matrix} \right] \) 的步骤为:
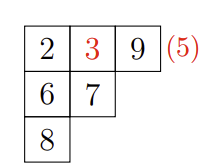
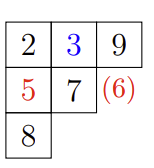
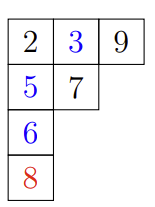
\(\text{Robinson-Schensted correspondence}\) 定理:
同时,我们设置另一个表,记录杨表中每一个位置是在第几轮被填上数的,我们可以通过这两个表还原出整个序列。
容易发现,我们所开的第二个表也是一个杨表,且和第一个杨表形态相同。
对于任意一组形态相同的杨表,我们都可以通过倒推的方式还原出一个唯一的序列,一个序列也可以产生一对唯一的杨表。
也就是说数组和一对杨表形成双射,有:
其中 \(\lambda \vdash n\) 是一个 \(n\) 的整数拆分,\(f_\lambda\) 是 \(\lambda\) 这个整数划分的填法数量。
例题
子序列问题
对于杨表 , 定义对于一个从 \(1\) 到 \(n\) 的排列 \(X=x_1,...,x_n\)。
\(P_X\) 中第一行的长度即为排列 \(X\) 的 最长上升子序列(LIS) 长度。注意,\(P\) 的第一行并不一定是 LIS 本身,所以不能直接利用杨表性质解决“LIS 划分”之类的问题。
对于一个排列 \(X\) 和它产生的杨表 \(P_X\),若 \(X^R\) 是 \(X\) 的翻转,那么 \(X^R\) 产生的杨表 \(P_{X^R}\) 即为 \(P_X\) 交换行列得到。
例如,对于排列 \(X=1,5,7,2,8,6,3,4\) 和 \(X^R=4,3,6,8,2,7,5,1\), 我们可得到如下杨表 :
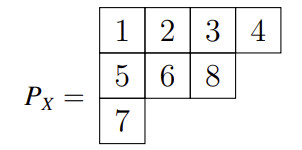
杨表 \(P_X\) 中的第一列长度即为排列 \(X\) 的 最长下降子序列(LDS) 长度。
定义长度不超过 \(k\) 的 \(LIS/LDS\) 长度为 \(k-LIS\) 和 \(k-LDS\), 此类问题我们同样可以用杨表来解决。对于 \(1-LIS\),显而易见最长的 \(1-LIS\) 子序列就是该序列的 \(LDS\),这也正是杨表的第一列;
由 \(\text{Dilworth}\) 引理可知,序列的最长上升子序列长度等于将其划分为若干个不上升子序列所需数量的最小值。
因此最长 \(k-LIS\) 子序列长度即为序列的前 \(k\) 长不相交下降子序列长度之和。
可以表示成 \(F(k)=\sum_{i=1}^{m}min(k,\lambda_i)\),即前 \(k\) 列的长度和。
CF1268B Domino for Young
首先考察第一个结论:如果一个杨表黑白染色后两种颜色的数量相等,那么其可以被多米诺骨牌密铺。
该结论的正确证明如下:从一个黑白染色后两种颜色的数量相等的杨表出发:
- 如果该杨表有两行长度相同、或两列高度相同,则我们可以填上一个骨牌使剩下的部分仍是杨表,且黑白格子数仍然相同(如下方左图);
- 如果没有,那么杨表形状如下方右图,其黑白颜色格子数一定不同,矛盾;
- 那么一个杨表一定能被填满。
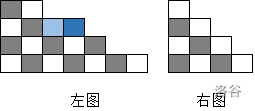
接着考虑当黑白格子个数不等时怎么做。我们考虑模仿上述过程,当没有两行长度相同或两列高度相同时,我们去掉最上方那个格子(其颜色一定是出现次数较多的一种)之后继续做,显然全程只会把出现较多的格子留空。
于是答案为两种颜色格子数之最小值的结论得证。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
long long X=0,w=1;
char c = getchar();
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9')X=X*10+c-'0',c=getchar();
return X*w;
}
int main(){
long long n=read(),black=0,white=0;
for(long long i=1;i<=n;i++){
long long a=read();
black+=(a/2),white+=(a/2);
if(i%2==1&&a%2==1)black+=1;
else if(i%2==0&&a%2==1)white+=1;
}
cout<<min(black,white);
return 0;
}
[CTSC2017]最长上升子序列
杨表裸题,按照如上方法暴力维护杨表即可拿到 \(95\) 分。
考虑为什么拿不到满分,因为暴力建杨表的复杂度是 \(O(\text{LDS}\times log\times n)\) 的可以被卡成 \(O(n^2 log\ n)\)。
我们发现如果一个点插入的位置是 \((x,y)\),有 \(x\times y\le n\),进而如果 \(x>\sqrt n\) 必然有 \(y\le \sqrt n\)。
因此我们可以维护两个杨表,同时将第二个杨表的比较符取反。
可以发现第二个杨表与第一个杨表的转置具有相同的形态,将第一个杨表中 \(\sqrt n\) 行以后的点放到第二个杨表中统计即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,q;
int a[50005],tree[50005],ans[200005];
inline void add(int x){
while(x<=n){
tree[x]++;x+=(x&-x);
}
}
inline int query(int x){
int res=0;
while(x){
res+=tree[x];x&=(x-1);
}return res;
}
struct Yang{
vector<vector<int> > yang;
bool is;
Yang(int _x){yang=vector<vector<int> >();is=_x;}
inline void insert(int x){
if(!is)x=-x;
for(int i=0;i<yang.size();i++){
auto &vec=yang[i];
auto it=(is?lower_bound(vec.begin(),vec.end(),x):upper_bound(vec.begin(),vec.end(),x));
if(it!=vec.end())swap(*it,x);
else {
vec.push_back(x);
if(is)add(vec.size());
else if(vec.size()>500)add(i+1);return ;
}
}
if(yang.size()==500)return ;
yang.push_back(vector<int>());
yang.back().push_back(x);
if(is==1)add(1);
}
inline void print(){
for(auto vec:yang){
for(auto it:vec)printf("%d ",it);
puts("");
}puts("---");
}
};
vector<pair<int,int> > qry[500005];
vector<int> vec;
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
Yang y1(0),y2(1);
for(int i=1;i<=q;i++){
int m,k;
scanf("%d%d",&m,&k);
qry[m].push_back(make_pair(i,k));
}
for(int i=1;i<=n;i++){
y1.insert(a[i]);y2.insert(a[i]);
for(auto it:qry[i])ans[it.first]=query(it.second);
}//y1.print();y2.print();
for(int i=1;i<=q;i++)printf("%d\n",ans[i]);
return 0;
}
[BJWC2018]最长上升子序列
一个基于杨表的暴力:
由杨表的构造过程可知,一个序列构建的杨表其第一行长度就是 LIS 长度。因此我们想知道:对于每个 \(1\le k \le n\),对于一个长为 \(n\) 的排列,有多少种排列使得杨表的第一行长度为 \(k\)。
\(\text{Robinson-Schensted correspondence}\) 定理指出,对于任何两个相同形状的杨表(填数的顺序可能不同),可以与排列建立一一对应。
因此我们要求的就是
通过 \(\text{Hook}\) 公式可以在 \(\Theta(n)\) 时间内计算。
因此如果枚举所有的整数划分,则可以在 \(\Theta(np(n))\) 的时间内解决本题。
注意 \(p(n) \sim \frac1{4n\sqrt 3}\exp \left(\pi \sqrt\frac{2n}3\right)\)p(n),这是一个效率相当优秀的亚指数算法。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
const int md=998244353;
int fac[105],inv[105];
inline void init(){
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++)fac[i]=1ll*fac[i-1]*i%md;
for(int i=2;i<=n;i++)inv[i]=1ll*(md-md/i)*inv[md%i]%md;
}
bool vis[105][105];
long long ans;
void dfs(int x,int lim,int pos){
if(!x){
// for(int i=1;i<=n;i++){
// for(int j=1;j<=n;j++)printf("%d ",vis[i][j]);puts("");
// }
int tmp=0,res=fac[n];
for(int i=1;vis[1][i];i++)tmp++;
for(int i=1;vis[i][1];i++){
for(int j=1;vis[i][j];j++){
int tot=1;
for(int t=i+1;vis[t][j];t++)tot++;
for(int t=j+1;vis[i][t];t++)tot++;res=1ll*res*inv[tot]%md;
}
}//cout<<" "<<1ll*res*res%md<<" "<<tmp<<endl;
ans=(ans+1ll*res*res%md*tmp)%md;return ;
}
for(int i=1;i<=lim&&i<=x;i++){
vis[pos][i]=1;dfs(x-i,i,pos+1);
}
for(int i=1;i<=lim&&i<=x;i++)vis[pos][i]=0;
}
int main(){
scanf("%d",&n);
init();
dfs(n,n,1);for(int i=1;i<=n;i++)ans=ans*inv[i]%md;
printf("%lld",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号