Lydon 分解与最小表示法
我们定义一个串是 \(\text{Lyndon}\) 串,当且仅当这个串的最小后缀就是这个串本身。
该命题等价于这个串是它的所有循环表示中字典序最小的。
引理 1:如果 \(u\) 和 \(v\) 都是 \(\text{Lyndon}\) 串并且 \(u<v\),则 \(uv\) 也是 \(\text{Lyndon}\) 串。
证明:
1、若 \(\operatorname{len}(u)\ge\operatorname{len}(v)\)
这时,\(u\) 和 \(v\) 这两个串在 \(\operatorname{len}(v)\) 之前就出现了不同的字符,所以有 \(v>uv\),又因为 \(v\) 是 \(\text{Lyndon}\) 串,所以 \(v\) 的所有后缀都大于 \(v\),所以 \(uv\) 的所有后缀都大于 \(uv\),故 \(uv\) 是 \(\text{Lyndon}\) 串。
2、若 \(\operatorname{len}(u)<\operatorname{len}(v)\)
若 \(u\) 不是 \(v\) 的前缀,那么有 \(v>uv\),得证。
若 \(u\) 是 \(v\) 的前缀,那么如果 \(v<uv\),则必有 \(v[\operatorname{len}(u)+1:]<v\)(也就是各自去掉了前 \(|u|\) 个字符),矛盾。
我们定义一个串 \(S\) 的 \(\text{Lyndon}\) 分解为一个字符串序列 \(A_1,A_2,\dots,A_m\),满足:
-
\(\forall i \in [1,m]∀i∈[1,m]\),满足 A_i是 \(\text{Lyndon}\) 串。
-
\(\forall i \in [1,m-1]∀i∈[1,m−1]\),满足 \(A_i\ge A_{i+1}\)
可以证明这种划分存在且唯一。
存在性证明:
初始令 \(m=|S|\) 并且 \(A_i=S[i]\),然后每次不断找到 \(A_i<A_{i+1}\) 并且合并为一个串。最后一定能使得所有的 \(A_i\ge A_{i+1}\)
实际上,通过这个证明,我们可以对其建出 \(SAM\) ,再通过 \(O(1)\) 求 \(parent\) 树上的 \(lca\) 比较两个后缀的大小即可在时间空间复杂度均视为 \(O(n)\) 的情况下求出一个字符串的 \(Lydon\) 分解。
引理2:若字符串 \(v\) 和字符 \(c\) 满足 \(vc\) 是某个 \(\text{Lyndon}\) 串的前缀,则对于字符 \(d>c\) 有 \(vd\) 是 \(\text{Lyndon}\) 串。
证明:
设该 \(\text{Lyndon}\) 串为 \(v+c+t\)。
则 \(\forall i \in [2,|v|],v[i:]+c+t>v+c+t\),也就是说 \(v[i:]+c\ge v\)。
所以 \(v[i:]+d>v[i:]+c\ge v\)。
同时因为 \(c>v[1]\),我们有 \(d>c>v[1]\)。
故 \(v+d\) 是一个 \(\text{Lyndon}\) 串。
Duval 算法
这个算法可以在 \(O(n)\) 时间复杂度,\(O(1)\) 空间复杂度内求出一个串的 \(\text{Lyndon}\) 分解。
该算法中我们仅需维护三个变量 \(i,j,k\)。
维持一个循环不变式:
-
\(s[:i-1]=s_1s_2\cdots s_g\) 是固定下来的分解,也就是 \(\forall l\in[1,g],s_l\) 是 \(\text{Lyndon}\) 串且 \(s_l>s_{l+1}\)
-
\(s[i,k−1]=t^h+v\times [h>1]\) 是没有固定的分解,满足 \(t\) 是 \(\text{Lyndon}\) 串,且 \(v\) 是 \(t\) 的可为空的不等于 \(t\) 的前缀,且有 \(s_g>s[i,k-1]\)
如下图:
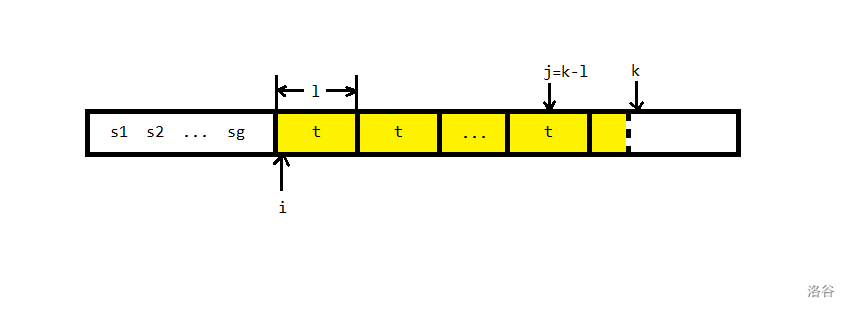
当前读入的字符是 \(s[k]\),令 \(j=k-|t|\)。
分三种情况讨论:
当 \(s[k]=s[j]\) 时,直接 \(k\leftarrow k+1,j\leftarrow j+1\),周期 \(k-j\) 继续保持。
当 \(s[k]>s[j]\) 时,由引理 2 可知 \(v+s[k]\) 是 \(\text{Lyndon}\) 串,由于 \(\text{Lyndon}\) 分解需要满足 \(s_i\ge s_{i+1}\),所以不断向前合并,最终整个 \(t^h+v+s[k]\) 形成了一个新的 \(\text{Lyndon}\) 串。
当 \(s[k]<s[j]\) 时,\(t^h\) 的分解被固定下来,算法从 \(v\) 的开头处重新开始。
复杂度分析:\(i\) 只会单调往右移动,同时 \(k\) 每次移动的距离不会超过 \(i\) 移动的距离,所以时间复杂度是 \(O(n)\) 的。
【模板】Lyndon 分解
点击查看代码
#include<bits/stdc++.h>
using namespace std;
char s[5000005];
int n,ans;
int main(){
scanf("%s",s+1);
n=strlen(s+1);
int i=1;
while(i<=n){
int j=i,k=i+1;
while(k<=n&&s[k]>=s[j]){
if(s[k]>s[j])j=i;
else j++;k++;
}
while(i<=j){
ans^=(i+k-j-1);
i+=k-j;
}
}printf("%d",ans);
return 0;
}
最小表示法
一个字符串的最小表示定义为其所有循环同构中字典序最小的串。
最小表示法可以使用 \(\text{Lyndon}\) 分解求出。
对于长度为 \(n\) 的字符串 \(s\),设 \(t=s+s\),对 \(t\) 进行 \(\text{Lyndon}\) 分解,找到首字符位置 \(\le n\) 且最大的 \(\text{Lyndon}\) 串,这个串的首字符即最小表示法的首字符。
【模板】最小表示法
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int s[5000005];
int n,ans;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&s[i]);
for(int i=1;i<=n;i++)s[i+n]=s[i];
int i=1;
while(i<=n){
int j=i,k=i+1;
while(k<=2*n&&s[k]>=s[j]){
if(s[k]>s[j])j=i;
else j++;k++;
}
while(i<=j){
i+=k-j;
if(i<=n)ans=i;
}
}
for(int i=0;i<n;i++)printf("%d ",s[i+ans]);
return 0;
}
[JSOI2019]节日庆典
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
char s[3000005];
int z[3000005];
void exkmp(){
int l=0,r=0;z[1]=n;
for(int i=2;i<=n;i++){
if(r>i)z[i]=min(z[i-l+1],r-i+1);
while(i+z[i]<=n&&s[i+z[i]]==s[z[i]+1])z[i]++;
if(i+z[i]-1>r)l=i,r=i+z[i]-1;
}
return ;
}
vector<int>now,nxt;
int main(){
scanf("%s",s+1);
n=strlen(s+1);exkmp();
for(int i=1;i<=n;i++){
now.push_back(i);
nxt.clear();
for(int j=0;j<now.size();j++){
int p=now[j];
bool flag=1;
while(!nxt.empty()){
int q=nxt.back();
if(s[i]>s[q+i-p])flag=0;
if(s[i]>=s[q+i-p])break;
nxt.pop_back();
}
if(flag&&(nxt.empty()||(i-p+1<p-nxt.back())))nxt.push_back(p);
}
now=nxt;
int pos=now[0];
for(int j=1;j<now.size();j++){
int x=now[j],k=pos+i-x;
if(z[k+1]>=i-k){
register int l=i-k;
if(z[l+1]<x-l-1&&s[l+z[l+1]+1]<s[z[l+1]+1])pos=x;
}
else if(s[z[k+1]+1]<s[k+z[k+1]+1])pos=x;
}
printf("%d ",pos);
}
return 0;
}


