PAT 1146 Topological Order

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

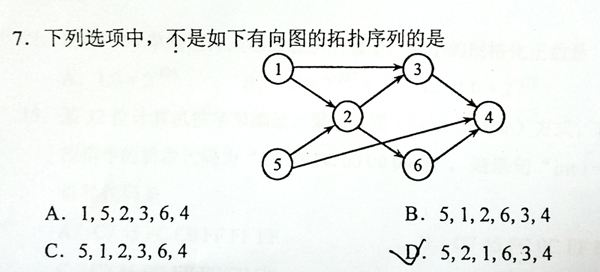
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:
Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

#include<iostream> //水题， 考虑入度即可
#include<vector>
using namespace std;
int main(){
	int n, m;
	cin>>n>>m;
	vector<vector<int>> v(n+1);
	vector<int> indegree(n+1, 0);
	vector<int> ans;
	for(int i=0; i<m; i++){
		int s, e;
		cin>>s>>e;
		v[s].push_back(e);
		indegree[e]++;
	}
	int k, a;
	cin>>k;
	for(int i=0; i<k; i++){
		vector<int> t=indegree;
		int flag=0;
		for(int j=0; j<n; j++){
			cin>>a;
			if(t[a]!=0)	flag=1;
			for(int p=0; p<v[a].size(); p++)
				t[v[a][p]]--;
		}
		if(flag==1) ans.push_back(i);
	}
	for(int i=0; i<ans.size(); i++)
		i==0?cout<<ans[i]:cout<<" "<<ans[i];
	return 0;
}