关于树状数组

一. 什么是树状数组？

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。

个人拙见：其实呢，是一种长的像树的可以高效查询子数组的和以及可以修改元素的数组。

 

二. 究竟该如何去实现它的功能呢？（以下是来自一个小白的认知，如有错误，不吝指正）

首先呢，A[]是一个数组，如果叫你求A的任意子数组的和，有个聪明的办法就是在读入A的数据时，创建数组B，B[i]是从A[0]到A[i]的和，然后呢，求子数组的和时就可以利用B数组的两个元素相减求得子数组的和， 就目前为止，该办法没什么毛病，可是呢，问题很快来了，如果A的元素会被修改呢，那数组B就要随之改变啊，如果A[i]改变，则B[i]以后的所有元素都要改变。那么树状数组可以避免去改变数组B吗，答案是NO，那为什么还用树状数组呢，因为他依然要改变B，但它改变的项会远远小于前面的做法。

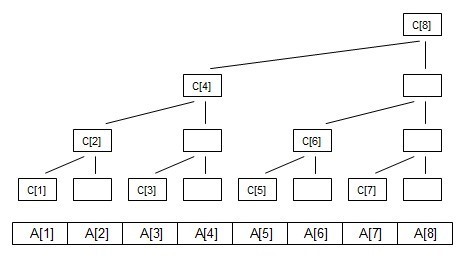
说到现在，才开始进入正题，如果我们依旧沿着前面的思路，创造一个数组C，但在这里C[i]不在是A[0]到A[i]的和了

看一下上面的图，

如果

C1 = A1

C2 = A1 + A2

C3 = A3

C4 = A1 + A2 + A3 + A4

C5 = A5

C6 = A5 + A6

C7 = A7

C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

...

好好，看到这里有同学估计和我一样脾气上来了，什么狗屁玩意啊，Ci到底等于什么啊，每一个Ci等于几个A元素的和，可是这几个A[i]的数目和Ci到底有什么关系呢。

稳定一下军心，首先Ci中的i写成二进制形式，比如C4吧，4写成二进制100，末尾有两个0，所以呢，等号右边有2^2个数，即C4管辖这A中的A1,A2,A3,A4这四个数，C4是他们的和。再比如C7,写成二进制111，末尾有零个0，所以等号右边有2^0=1个数，即C7管辖着A中的A7着一个数，C7是他们的和。那有人问了，我程序中还要这么麻烦啊，先求二进制，然后数末尾的0，你有毒吧。其实呢，有个现成的东西，

int lowbit(int x){

return x&-x;

}

lowbit 返回的就是x在二进制下末尾的0的个数。

那如何每次更新C[i]呢，比如说吧，输入或者更新了A1吧，收先C1肯定要变吧，即A1+k或者A1-k的话，C中所有含有A1的项都要+k或者-k吧，那么从上面的式子来看，C2，C4,C8都也要变，可是用程序怎么写呢，好，更新A1加k，令i=1,Ci+k,然后呢，i=i+lowbit(i)，看看i是不是等于2，Ci+k,然后继续下去i=i+lowbit(i),看看是不是i=4.

用代码实现

void update(int x, int v) {

    for(int i = x; i < maxn; i += lowbit(i))

        c[i] += v;

}

其中x是表示Ax发生变化，v表示Ax发生的变化。

那么如何求sum[i]呢（sum[i]表示A[0]到A[i]的和）

比如sum[7]=(A[7])+(A[6]+A[5])+(A1 + A2 + A3 + A4)=C7+C6+C4

 规律跟上面差不多，反过来的，sum[i]=Ci+sum[i-lowbit(i)];

用代码实现

int getsum(int x) {

    int sum = 0;

    for(int i = x; i >= 1; i -= lowbit(i))

        sum += c[i];

    return sum;

}

 

以上就是本菜鸟的所以拙见了，希望大家多多包含。