noip2013 华容道

 

题目描述

 

【问题描述】

 

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面， 华容道是否根本就无法完成，如果能完成， 最少需要多少时间。

 

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

 

1. 在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；

2. 有些棋子是固定的，有些棋子则是可以移动的；

3. 任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

 

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

 

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的， 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次

 

玩的时候， 空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi列，目标位置为第 TXi 行第 TYi 列。

 

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

 

输入输出格式

输入格式：

 

 

输入文件为 puzzle.in。

 

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

 

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

 

 

输出格式：

 

 

输出文件名为 puzzle.out。

 

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

 

 

 

输入输出样例

 

输入样例#1：

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

输出样例#1：

2
-1

 

说明

 

【输入输出样例说明】

 

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

 

1. 第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

 

移动过程如下：

 

 

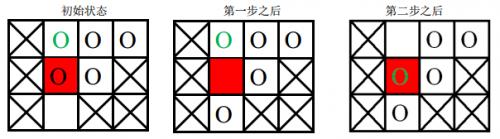
2. 第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

 

 

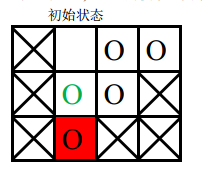
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置， 游戏无

 

法完成。

 

【数据范围】

 

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；

 

对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；

 

对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

 

solution

---

暴力(70)：

定义f[x1][y1][x2][y2]为空格在(x1,y1)，目标棋子在(x2,y2)，时的最小步数

之后bfs就行

正解：

也是bfs

预处理出来数组 g[x][y][k][kk]  1<=k,kk<=4

意义是 当前棋子在(x,y)白棋子在k方向(上下左右)，想要走到kk方向的最小步数

 

之后对于每次询问

首先把白格子挪到目标旗子周围，之后把目标棋子挪到目标位置，bfs利用g[][][][]数组

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int DUI=20000006;
const int INF=0x7fffffff;

inline int minn(int a,int b){return a<b?a:b;}

struct Queue
{
    int x,y;
};

queue<Queue> q;
int n,m,Q,qqq;
int bx[6]={0,-1,1,0,0,0};
int by[6]={0,0,0,-1,1,0};// 1 上 2 下 3 左 4 右 
int f[36][36][6],ha[6],flag[36][36],vis[36][36][6];
int a[36][36],g[36][36][6][6],d[36][36];
int whx,why,sx,sy,tx,ty;

void out11();

void chu()
{
    mem(g,60);
    qqq=g[0][0][0][0];
    Queue now;
    int x,y;
    for(int i=1;i<=n;++i)
      for(int j=1;j<=m;++j)
      {
          if(a[i][j]==0)
            continue;
        for(int bai=1;bai<=4;++bai)
        {//printf("saafsffas\n");
                if( (i+bx[bai]<1) || (i+bx[bai]>n) || (j+by[bai]<1) || (j+by[bai]>m) || (a[i+bx[bai]][j+by[bai]]==0) )
                  continue;
          for(int tt=1;tt<=4;++tt)
          {
                    if( (i+bx[tt]<1) || (i+bx[tt]>n) || (j+by[tt]<1) || (j+by[tt]>m) || (a[i+bx[tt]][j+by[tt]]==0) )
                      continue;
                    //printf("i=%d j=%d\n",i,j);
                    if(bai==tt)
                    {
                        g[i][j][bai][tt]=0;
                      continue;
                    }
                    
                    
                    
                    while(!q.empty())q.pop();
                    mem(d,60);mem(flag,0);
                    sx=i+bx[bai];sy=j+by[bai];
                    tx=i+bx[tt];ty=j+by[tt];
                    d[sx][sy]=0;flag[sx][sy]=1;
                    q.push((Queue){sx,sy});
                    while(!q.empty())
                    {
            
                        now=q.front();q.pop();
                        x=now.x;y=now.y;flag[x][y]=0;
                        //if(x==tx&&y==ty)
                        //  break;
                        
                        for(int k=1;k<=4;++k)
                        {
                            if(x+bx[k]<1||x+bx[k]>n||y+by[k]<1||y+by[k]>m||a[x+bx[k]][y+by[k]]==0|| (x+bx[k]==i&&y+by[k]==j) )
                              continue;
                            //printf("sdasdasd\n");
                            if(d[x+bx[k]][y+by[k]]>d[x][y]+1)
                            {
                                d[x+bx[k]][y+by[k]]=d[x][y]+1;
                                if(!flag[x+bx[k]][y+by[k]])
                                {
                                    q.push((Queue){x+bx[k],y+by[k]});
                                    flag[x+bx[k]][y+by[k]]=1;
                                }
                            }
                        }
                    }
                    
                    //g[i][j][bai][tt]=d[tx][ty]+1;
                    g[i][j][bai][tt]=d[tx][ty];
                    
                    //out11();
                    
                    //printf("i=%d j=%d k=%d l=%d g[][][][]=%d\n",i,j,bai,tt,g[i][j][bai][tt]);
                }
            }
        }
}// yes

int bfs1()
{
    Queue now;
    int x,y;
    mem(d,60);
    while(!q.empty())q.pop();
    mem(flag,0);
    d[whx][why]=0;flag[whx][why]=1;
    q.push((Queue){whx,why});
    while(!q.empty())
    {
        now=q.front();q.pop();
        x=now.x;y=now.y;flag[x][y]=0;
        for(int k=1;k<=4;++k)
        {
            if(x+bx[k]<1||x+bx[k]>n||y+by[k]<1||y+by[k]>m||a[x+bx[k]][y+by[k]]==0|| (x+bx[k]==sx&&y+by[k]==sy) )
              continue;
            if(d[x+bx[k]][y+by[k]]>d[x][y]+1)
            {
                d[x+bx[k]][y+by[k]]=d[x][y]+1;
                if(!flag[x+bx[k]][y+by[k]])
                {
                    q.push((Queue){x+bx[k],y+by[k]});
                    flag[x+bx[k]][y+by[k]]=1;
                }
            }
        }
    }
    
    for(int i=1;i<=4;++i)
      if(d[sx+bx[i]][sy+by[i]]<qqq)
        return 1;
    return 0;
}

struct son
{
    int x,y,k;
};
queue<son> dui;

int bfs2()
{
    son now;
    int x,y,nowk;
    mem(f,60);mem(vis,0);
    for(int i=1;i<=4;++i)
    {
      if(sx+bx[i]<1||sx+bx[i]>n||sy+by[i]<1||sy+by[i]>m||a[sx+bx[i]][sy+by[i]]==0||d[sx+bx[i]][sy+by[i]]==qqq)
        continue;
      f[sx][sy][i]=d[sx+bx[i]][sy+by[i]];
      vis[sx][sy][i]=1;
      //printf("ssdad=%d\n",d[sx+bx[i]][sy+by[i]]);
      dui.push((son){sx,sy,i});
    }
    
    //out11();
    
    while(!dui.empty())
    {
        now=dui.front();dui.pop();
        x=now.x;y=now.y;nowk=now.k;
        vis[x][y][nowk]=0;
        
        for(int i=1;i<=4;++i)
        {
            if(x+bx[i]<1|| (x+bx[i]>n) || (y+by[i]<1) || (y+by[i]>m) || (a[x+bx[i]][y+by[i]]==0) )
              continue;
            //printf("hhahahahahha\n");
            int temp1=f[x+bx[i]][y+by[i]][ha[i]];
            int temp2=f[x][y][nowk]+1+g[x][y][nowk][i];
            //printf("%d %d\n",temp1,temp2);
            if(temp1>temp2)
            {
                
                f[x+bx[i]][y+by[i]][ha[i]]=f[x][y][nowk]+1+g[x][y][nowk][i];
                if(!vis[x+bx[i]][y+by[i]][ha[i]])//////????????
                {
                    dui.push((son){x+bx[i],y+by[i],ha[i]});
                    vis[x+bx[i]][y+by[i]][ha[i]]=1;
                }
            }
        }
    }
    
    //out11();
    
    int ans=INF;
    for(int i=1;i<=4;++i)
      ans=minn(ans,f[tx][ty][i]);
    return ans;
}

void out11()
{
    printf("\n");
    for(int k=1;k<=4;++k)
    {
    for(int i=1;i<=n;++i)
    {
      for(int j=1;j<=m;++j)
        printf("%d ",f[i][j][k]);
      printf("\n");
    }
    printf("\n");
  }
  
    /*for(int i=1;i<=n;++i)
    {
    for(int j=1;j<=m;++j)
      printf("%d ",d[i][j]);
    printf("\n");
  }*/
    /*for(int i=1;i<=n;++i)
      for(int j=1;j<=m;++j)
        for(int k=1;k<=4;++k)
          for(int l=1;l<=4;++l)
            if(g[i][j][k][l]!=qqq)
              printf("i=%d j=%d k=%d l=%d g[][][][]=%d\n",i,j,k,l,g[i][j][k][l]);*/
    printf("\n");
}

int main(){
    
    //freopen("1.txt","r",stdin);
    
    scanf("%d%d%d",&n,&m,&Q);
    for(int i=1;i<=n;++i)
      for(int j=1;j<=m;++j)
        scanf("%d",&a[i][j]);
    chu();
    ha[1]=2;ha[2]=1;ha[3]=4;ha[4]=3;
    
    //out11();
    
    while(Q--)
    {
        scanf("%d%d%d%d%d%d",&whx,&why,&sx,&sy,&tx,&ty);
        if(sx==tx&&sy==ty)
        {
            printf("0\n");
            continue;
        }
        if(bfs1()==0)
        {
            printf("-1\n");
            continue;
        }
        int temp=bfs2();
        if(temp>=qqq)
        {
            printf("-1\n");
            continue;
        }
        printf("%d\n",temp);
    }
    
    //while(1);
    return 0;
}