bzoj 3144: [Hnoi2013]切糕
Description
.jpg)
Input
第一行是三个正整数P,Q,R,表示切糕的长P、 宽Q、高R。第二行有一个非负整数D,表示光滑性要求。接下来是R个P行Q列的矩阵,第z个 矩阵的第x行第y列是v(x,y,z) (1≤x≤P, 1≤y≤Q, 1≤z≤R)。
100%的数据满足P,Q,R≤40,0≤D≤R,且给出的所有的不和谐值不超过1000。
Output
仅包含一个整数,表示在合法基础上最小的总不和谐值。
Sample Input
2 2 2
1
6 1
6 1
2 6
2 6
1
6 1
6 1
2 6
2 6
Sample Output
6
HINT
最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1
solution
用a[n][m][h]记录不和谐值
建模:
1.将 S 与最底层的点连 一条a[i][j][1] 的边
2.将每一个轴上的每一个点与其上面的点连一条 容量为上一个点不和谐值的边
3.将最上层的点 与 T点连一条 INF 的边
4.最重要的:为了限制 |f(x,y)-f(x1,y1)|<=D 这个条件,我们将每一个点向 与它相邻的 并且比它低D的 点连一条INF的边(当然 没有就不用连了)
证明其正确性:
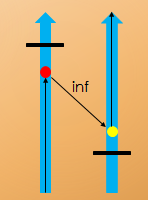
当两个截点d>D时,还会有增光路
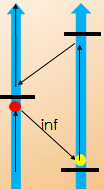
而如果在右边轴上面>D的地方截的话,还会有增广路

而如果在<=D的地方截的话,>D截的点又没有了必要

1 #include<cstdio> 2 #include<cstring> 3 #include<queue> 4 #include<iostream> 5 #define mem(a,b) memset(a,b,sizeof(a)) 6 #define ll long long 7 #define dd double 8 using namespace std; 9 const int INF=(1<<31)-1; 10 const int N=2006; 11 inline int minn(int a,int b){return a<b?a:b;} 12 struct son 13 { 14 int u,v,next; 15 int w; 16 }; 17 son a1[3000006]; 18 int first[3000006],e; 19 void addbian(int u,int v,int w) 20 { 21 a1[e].v=v; 22 a1[e].w=w; 23 a1[e].u=u; 24 a1[e].next=first[u]; 25 first[u]=e++; 26 } 27 void Link(int u,int v,int w) 28 { 29 addbian(u,v,w); 30 addbian(v,u,0); 31 } 32 void Match(int u,int v,int w) 33 { 34 addbian(u,v,w); 35 addbian(v,u,w); 36 } 37 38 int n,m,h,D; 39 int S,T,ha[46][46][46]; 40 int a[46][46][46]; 41 42 int dui[1000001],he,en; 43 inline void clear(){he=1;en=0;} 44 inline void push(int x){dui[++en]=x;} 45 inline int top(){return dui[he];} 46 inline void pop(){++he;} 47 inline bool empty(){return en>=he?0:1;} 48 49 int dep[64666]; 50 int bfs() 51 { 52 mem(dep,0);clear(); 53 dep[S]=1;push(S); 54 while(!empty()) 55 { 56 int now=top();pop(); 57 for(int i=first[now];i!=-1;i=a1[i].next) 58 { 59 int temp=a1[i].v; 60 if(!a1[i].w||dep[temp])continue; 61 dep[temp]=dep[now]+1; 62 push(temp); 63 if(temp==T)return 1; 64 } 65 } 66 return 0; 67 } 68 69 int dfs(int x,int val) 70 { 71 if(x==T)return val; 72 int val2=val,k; 73 for(int i=first[x];i!=-1;i=a1[i].next) 74 { 75 int temp=a1[i].v; 76 if(!a1[i].w||dep[temp]!=dep[x]+1||!val2)continue; 77 k=dfs(temp,minn(val2,a1[i].w)); 78 if(!k){dep[temp]=0;continue;} 79 a1[i].w-=k;a1[i^1].w+=k;val2-=k; 80 } 81 return val-val2; 82 } 83 84 int Dinic() 85 { 86 int ans=0; 87 while(bfs()) 88 ans+=dfs(S,INF); 89 return ans; 90 } 91 92 int main(){ 93 mem(first,-1); 94 scanf("%d%d%d",&n,&m,&h); 95 scanf("%d",&D); 96 for(int k=1;k<=h;++k) 97 for(int i=1;i<=n;++i) 98 for(int j=1;j<=m;++j) 99 {scanf("%d",&a[i][j][k]);ha[i][j][k]=(k-1)*n*m+(i-1)*m+j;} 100 101 S=0;T=n*m*h+1; 102 103 for(int i=1;i<=n;++i) 104 for(int j=1;j<=m;++j) 105 Link(S,ha[i][j][1],a[i][j][1]); 106 107 for(int k=1;k<h;++k) 108 for(int i=1;i<=n;++i) 109 for(int j=1;j<=m;++j) 110 Link(ha[i][j][k],ha[i][j][k+1],a[i][j][k+1]); 111 112 for(int i=1;i<=n;++i) 113 for(int j=1;j<=m;++j) 114 Link(ha[i][j][h],T,INF); 115 116 for(int k=D;k<=h;++k) 117 for(int i=1;i<=n;++i) 118 for(int j=1;j<=m;++j) 119 { 120 if(i>1)Link(ha[i][j][k],ha[i-1][j][k-D],INF); 121 if(i<n)Link(ha[i][j][k],ha[i+1][j][k-D],INF); 122 if(j>1)Link(ha[i][j][k],ha[i][j-1][k-D],INF); 123 if(j<m)Link(ha[i][j][k],ha[i][j+1][k-D],INF); 124 } 125 126 printf("%d",Dinic()); 127 //while(1); 128 return 0; 129 }



