2009国家集训队 employ人员雇佣

Description

作为一个富有经营头脑的富翁，小L决定从本国最优秀的经理中雇佣一些来经营自己的公司。这些经理相互之间合作有一个贡献指数,（我们用Ei,j表示i经理对j经理的了解程度），即当经理i和经理j同时被雇佣时，经理i会对经理j做出贡献，使得所赚得的利润增加Ei,j。当然，雇佣每一个经理都需要花费一定的金钱Ai，对于一些经理可能他做出的贡献不值得他的花费，那么作为一个聪明的人，小L当然不会雇佣他。 然而，那些没有被雇佣的人会被竞争对手所雇佣，这个时候那些人会对你雇佣的经理的工作造成影响，使得所赚得的利润减少Ei,j（注意：这里的Ei,j与上面的Ei,j 是同一个）。 作为一个效率优先的人，小L想雇佣一些人使得净利润最大。你可以帮助小L解决这个问题吗？

Input

第一行有一个整数N<=1000表示经理的个数 第二行有N个整数Ai表示雇佣每个经理需要花费的金钱 接下来的N行中一行包含N个数，表示Ei,j，即经理i对经理j的了解程度。（输入满足Ei,j=Ej,i）

Output

第一行包含一个整数，即所求出的最大值。

Sample Input

3
3 5 100
0 6 1
6 0 2
1 2 0

Sample Output

1
【数据规模和约定】
20%的数据中N<=10
50%的数据中N<=100
100%的数据中 N<=1000， Ei,j<=maxlongint, Ai<=maxlongint
 
solution
像 happiness 那道题一样建图：
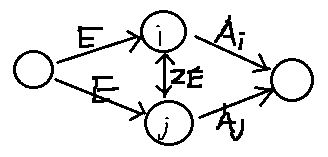
最后要用Dinic跑，EK会超时.........
  1 #include<cstdio>
  2 #include<cstring>
  3 #include<queue>
  4 #include<iostream>
  5 #define mem(a,b) memset(a,b,sizeof(a))
  6 #define ll long long
  7 #define dd double
  8 using namespace std;
  9 const int INF=(1<<31)-1;
 10 const int N=2006;
 11 inline int minn(int a,int b){return a<b?a:b;}
 12 struct son
 13 {
 14     int u,v,next;
 15     int w;
 16 };
 17 son a1[3000006];
 18 int first[3000006],e;
 19 void addbian(int u,int v,int w)
 20 {
 21     a1[e].v=v;
 22     a1[e].w=w;
 23     a1[e].u=u;
 24     a1[e].next=first[u];
 25     first[u]=e++;
 26 }
 27 void Link(int u,int v,int w)
 28 {
 29     addbian(u,v,w);
 30     addbian(v,u,0);
 31 }
 32 void Match(int u,int v,int w)
 33 {
 34     addbian(u,v,w);
 35     addbian(v,u,w);
 36 }
 37 
 38 int n,S,T;
 39 int sumE;
 40 int A[N];
 41 int E[N][N];
 42 int sum[N];
 43 
 44 int dui[10000001],he,en;
 45 inline void push(int x){dui[++en]=x;}
 46 inline bool empty(){return en>=he?0:1;}
 47 inline int top(){return dui[he];}
 48 inline void pop(){++he;}
 49 inline void clear(){he=1;en=0;}
 50 
 51 int dep[N];
 52 int bfs()
 53 {
 54     mem(dep,0);clear();
 55     dep[S]=1;push(S);
 56     while(!empty())
 57     {
 58         int now=top();pop();
 59         for(int i=first[now];i!=-1;i=a1[i].next)
 60         {
 61             int temp=a1[i].v;
 62             if(!a1[i].w||dep[temp])continue;
 63             dep[temp]=dep[now]+1;
 64             push(temp);
 65             if(temp==T)return 1;
 66         }
 67     }
 68     return 0;
 69 }
 70 
 71 int dfs(int x,int val)
 72 {
 73     if(x==T)return val;
 74     int val2=val,k;
 75     for(int i=first[x];i!=-1;i=a1[i].next)
 76     {
 77         int temp=a1[i].v;
 78         if(!a1[i].w||dep[temp]!=dep[x]+1||!val2)continue;
 79         k=dfs(temp,minn(val2,a1[i].w));
 80         if(!k){dep[temp]=0;continue;}
 81         a1[i].w-=k;a1[i^1].w+=k;val2-=k;
 82     }
 83     return val-val2;
 84 }
 85 
 86 int Dinic()
 87 {
 88     int ans=0;
 89     while(bfs())
 90       ans+=dfs(S,INF);
 91     return ans;
 92 }
 93 
 94 int main(){
 95     mem(first,-1);
 96     scanf("%d",&n);
 97     for(int i=1;i<=n;++i)scanf("%d",&A[i]);
 98     for(int i=1;i<=n;++i)
 99       for(int j=1;j<=n;++j)
100       {
101             scanf("%d",&E[i][j]);
102             sum[i]+=E[i][j];
103         }
104     
105     for(int i=1;i<=n;++i)
106       for(int j=i+1;j<=n;++j)
107         sumE+=E[i][j];
108     sumE*=2;
109     
110     S=0;T=n+1;
111     
112     for(int i=1;i<=n;++i)
113       Link(S,i,sum[i]);
114     for(int i=1;i<=n;++i)
115       Link(i,T,A[i]);
116     for(int i=1;i<=n;++i)
117       for(int j=i+1;j<=n;++j)
118         Match(i,j,2*E[i][j]);
119     
120     printf("%d",sumE-Dinic());
121     //while(1);
122     return 0;
123 }
code

 

posted @ 2017-07-31 07:47  A_LEAF  阅读(152)  评论(0)  编辑  收藏  举报