PointCNN: Convolution On X-Transformed Points
CNN之所以获得如此大的成功,关键在于他的Conv操作,该操作可以利用图像中密集表示的数据中的局部相关性,得到局部集合结构。此处的想法就是可不可以将其在PointCloud中应用该种想法。
\(\mathcal{X}-Conv\)来鹅城只为两件事:
- 对每个代表点周围的点特征做集成。
- 在隐空间对输入做重排去除输入顺序的影响。
上面两件事的作用可以类比为CNN里面的Conv操作。
作者提出了一种在卷积角度处理点云问题的框架,其中最关键的部分被称为\(\mathcal{X}-Conv\),他的主要作用就是解决了上面两件事。

在上图(i)中,每个网格单元关联一个特征。在ii-iv,这些点是从局部邻域采样的,类似于i中的局部面片,每个点都与特征、顺序索引和坐标关联这三个要素相连。
我们在上图中展示了点云应用在卷积上的问题和挑战。假设再上图的ii-iv上的C维无序集合的输入特征都是相同的\(\mathbb{F}=\{f_a,f_b,f_c,f_d\}\),而且我们有一个形状为\(4\times C\)的kernel \(K=[k_\alpha,k_\beta,k_\gamma,k_\delta]^T\)
上图ii-iv是点云的形式:
ii和iii虽然feature的输入顺序相同,但是feature的形状不同,此时就需要网络可以区分出来他们两个的不同之处。iii和iv虽然feature的输入顺序不同,但是feature的形状相同,此时就需要网络可以去除出来输入顺序对他们两个的影响。
由上图1a可得,由于卷积操作的性质,在所有情况下\(f_{ii},f_{iii}\)的计算结果是相等的,\(f_{iii},f_{iv}\)的操作结果是不相等的。很显然可以得出结论,直接卷积会导致原始信息丢失空间信息并且使得卷积的结果对于顺序很敏感。
解决方案 - Beg - 在隐空间对输入做重排去除输入顺序的影响
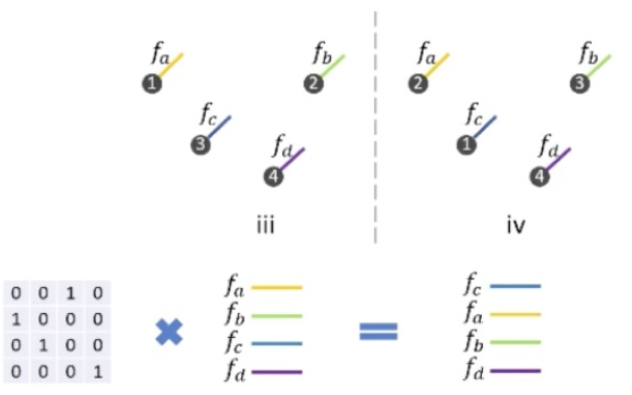
本文作者思路是让网络去学习一个转置矩阵\(\mathcal{X}\),该矩阵可以对某个特定顺序的输入进行处理,得到一个与顺序无关的feature。输入数据经过\(\mathcal{X}\)相乘之后,在执行Convolution的操作,比如图1中的iii,他的feature的顺序是abcd,经过和转置矩阵\(\mathcal{x}\)相乘之后,得到了某一种顺序能和图iv的这种排列顺序相等。此时我们就做到了上述的第二点,消除掉输入顺序对识别结果的不良影响。\(\color{red}{这样消除会不会同样消除掉空间信息呢?}\)感觉应该是不会的,他不是那种max-pooling操作,它是通过\(\mathcal{X}\)抵消顺序的。
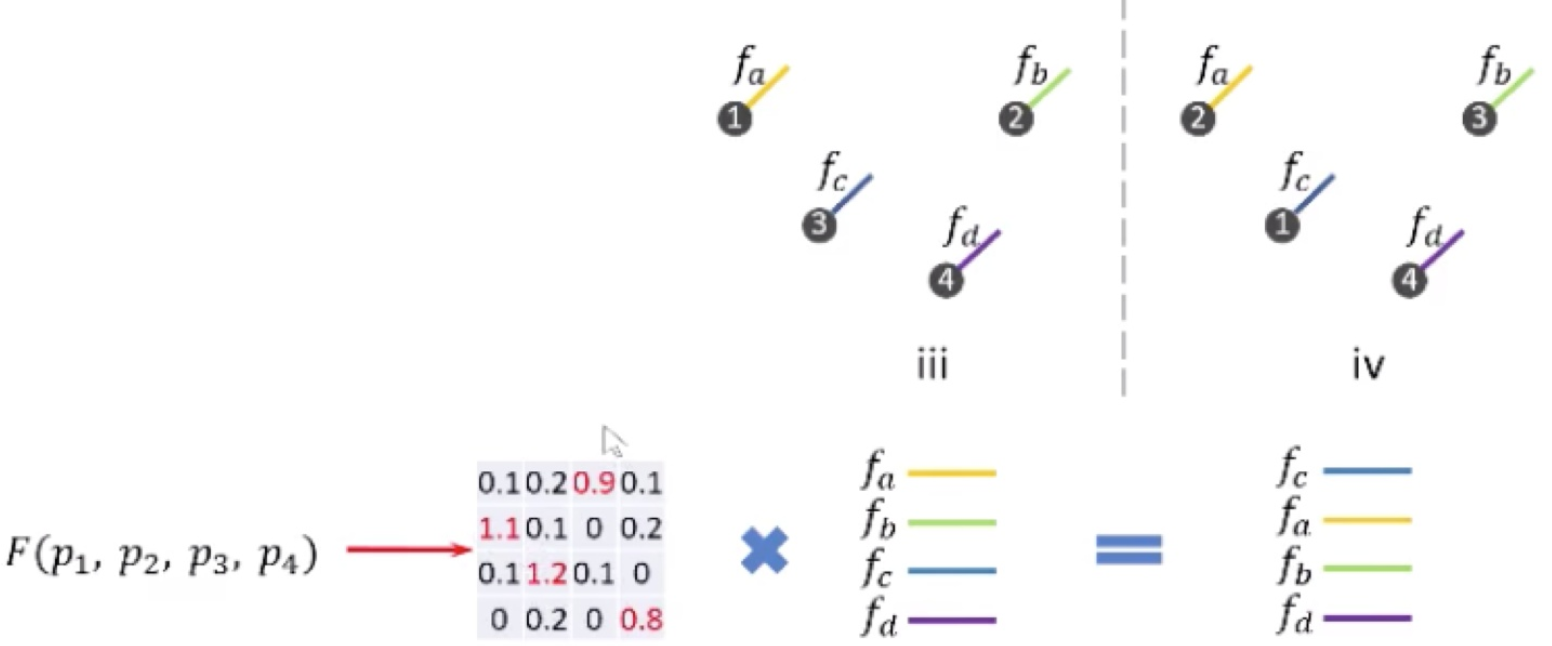
- 在结构信息相同的时候,尽管顺序信息不同,网络可以学到一种特征,形成针对性的矩阵,同结构化的点云,可以拥有相同顺序的
feature。 - 在顺序信息相同的时候,但结构信息不同,
经过矩阵计算得到的feature是不同的
对网络进行训练之后发现,矩阵并没有二值化,这也是一个待解决的问题,虽然没有成功二值化,但是这样的特征也可以理解为这个矩阵学到了如何在点云中提取feature的权重。
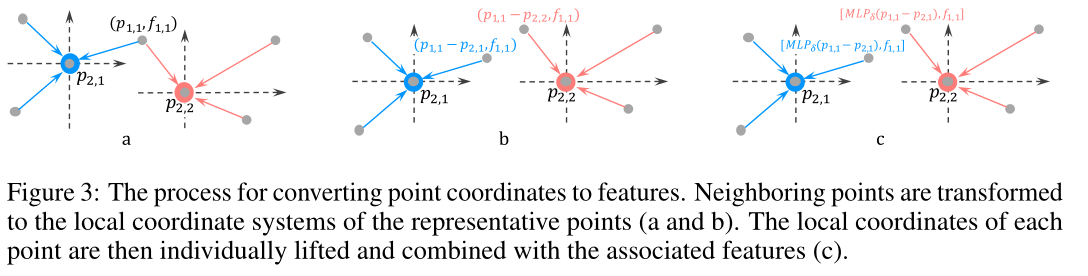
PointCNN对点云数据做平移不变性的操作,就是在中心点查到k近邻之后,用其周围点的坐标信息减去中心点的坐标信息,得到局部坐标系,将每个点的局部坐标系单独提升,并结合相关特征。这样就消除了整体的变化导致局部的变化,让网络学到的东西产生变化。
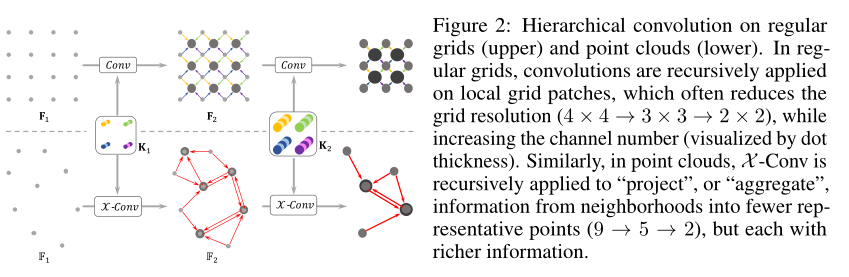
基于栅格的CNN的输入是一个\(F_1\)的特征图形状为\(R_1\times R_1\times C_1\)(如上图的\(F_1\)),其中的\(R_1\)是空间分辨率,\(C_1\)是特征的通道数。卷积核\(K\)的形状为\(K\times K\times C_1\times C_2\)将其与\(F_1\)形状为\(K\times K\times C_1\)local patch做卷积,产生一个形状为\(R_2\times R_2\times C_2\)的feature map。注意到图2的上部\(R_1=4,K=2,R_2=3\)。和\(F_1\)相比,\(F_2\)的分辨率一般都是比较低的\((R_2<R_1)\),但channels一般是比较高的\((C_2>C_1)\),编码到高级别的语义信息,这个过程是递归的,图越来越小,但深度越来越高。
PointCNN的输入是\(\mathbb{F}_1=\{(p_{1,i},f_{1,i}):i=1,2,\dots,N_1\}\),即点集\(\{p_{1,i}:p_{1,i}\in\mathbb{R}^{Dim}\}\),每个点与特征\(\{f_{1,i}:f_{1,i}\in\mathbb{R}^{C_1}\}\)相关联。了解过基于网格的CNN分层构造之后,我们希望在\(\mathbb{F}_1\)上应用X-Conv以获得更加高级别的表示\(\mathbb{F}_2=\{(p_{2,i},f_{2,i}:f_{2,i})\in\mathbb{R}^{C_2},i=1,2,\dots,N_2\}\),其中\(\{p_{2,i}\}\)是\(\{p_{1,i}\}\)的一组代表点,\(\mathbb{F}_2\)和\(\mathbb{F}_1\)相比有更小的分辨率和更深的通道数(\(N_2<N_1,C_2>C_1\))。当递归应用将\(\mathbb{F}_1\)转换为\(\mathbb{F}_2\)的\(\mathcal{X}-Conv\)过程中,具有特征的输入点被投影或聚合为更少的点\((9\rightarrow 5\rightarrow 2,如上图2所示)\),但每个点都有更加丰富的特征信息(点的颜色越来越深,大小越来越大)。
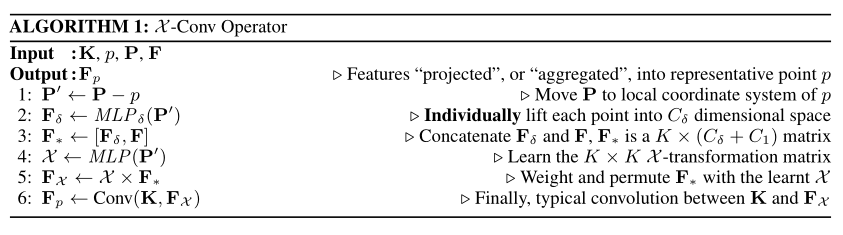
根据上图介绍\(\mathcal{X}-Conv\)如何利用空间局部相关性。
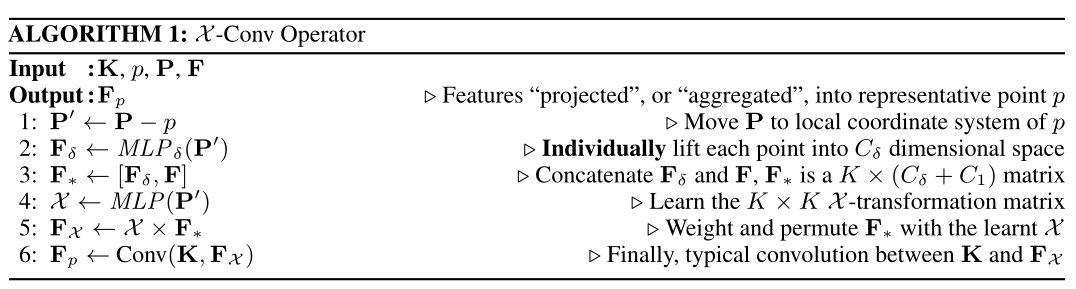
为了利用欧氏空间CNN卷积的那种空间局部相关性,\(\mathcal{X}-Conv\)在局部进行操作,由于输出特征应该和代表点\(\{p_{2,i}\}\)相关联,因此\(\mathcal{X}-Conv\)将\(\{p_{1,i}\}\)的邻域点和相关的特征作为输入。为了简单起见,我们将\(\{p_{2,i}\}\)中的一个代表点表示为\(p\),\(p\)的feature表示为\(f\),并将\(\{p_{1,i}\}\)的\(K\)个近邻点表示为\(\mathbb{N}\),因此对于\(p\)的\(\mathcal{X}-Conv\)的输入就是\(\mathbb{S}=\{(p_i,f_i):p_i\in\mathbb{N}\}\)。注意到\(\mathbb{S}\)是一个无序集合,在不丧失一般性的情况下,\(\mathbb{S}\)可以被转换成\(k\times Dim\)的矩阵\(P=(p_1,p_2,\dots,p_K)^T\),和\(K\times C_1\)的矩阵\(F=(f_1,f_2,\dots,f_K)^T\),\(K\)代表一个可训练的卷积核。经过上述,我们希望可以计算出特征\(F_p\),即输入特征到代表点\(p\)的投影或聚合。我们在上面的Algorithm中详细的介绍了\(\mathcal{X}-Conv\)运算符,并简要的总结如下:
\(MLP_\delta\)是类似PointNet的对每个点进行处理的多层感知机。并且构成\(\mathcal{X}-Conv\)的所有操作(Conv,MLP,matrix multiplication,\(MLP_\delta\))都是可微的,所以其本身也是可微的,可以插入到神经网络开始训练。
注意:
\(\mathcal{X}-Conv\)设计用于局部点区域,输出不应该取决于点\(p\)及其相邻点的绝对位置,而应该取决于他们的相对位置。所以我们在算法的第一步就实现了局部坐标系的操作,定义输出特征的就是相邻点的局部坐标和他们相关联的特征,然而局部特征的维度和表示方法和相关特征的表示方法是不同的。为了解决这个问题,我们首先将坐标系提高的更高的维度和更抽象的表示(第二行),然后将其与相关特征(第三行)结合起来进行进一步的处理。
\(MLP_\delta\)这个提高坐标点维度的方法和PointNet里面的方法是一致的,不同之处是提升特征的维度的方法没有经过对称函数的处理,取而代之的是,他们通过\(\mathcal{X}-transformation\)与相关特征一起进行加权和排列,\(\mathcal{X}-transformation\)是在所有邻域中共同学习的。\(\mathcal{X}\)取决于输入点的顺序(第四步),因为\(\mathcal{X}\)应该根据输入点对\(F_*\)进行排列,因此\(\mathcal{X}\)必须知道输入的特定顺序。对于没有任何附加信息的输入点云,第一层的\(\mathcal{X}-Conv\)进用于获取\(F_\delta\)
输入:
- \(P=(p_1,p_2,\dots,p_K)^T\),代表邻居点
- \(F=(f_1,f_2,\dots,f_K)^T\),代表邻居点的
feature - \(K=[k_\alpha,k_\beta,k_\gamma,k_\delta]^T\),卷积的kernel。
- \(p\),代表目标点
为了计算出\(p\)的feature,首先确定其邻居点集\(P\)(使用FPS,或KNN),按照以上算法操作:
根据上述不同用途的采样点方案对数据进行点采样得到\(p\)
- 将\(p\)的邻居节点的坐标转化为相对于\(p\)的坐标:\(P'\leftarrow P-p\)
- 使用\(MLP_\delta\),将上一步得到的邻居节点转化为
feature信息:\(F_\delta\leftarrow MLP_\delta(P')\) - 讲转化得到的
feature和邻居自己的关于点信息feature,得到新的feature:\(F_*\leftarrow [F_\delta,F]\) - 用\(MLP\)计算特定输入顺序的对应矩阵,以进行输入顺序无关化处理:\(\mathcal{X}\leftarrow MLP(P')\)
- 使用上一步计算出来的矩阵对特征进行顺序无关化处理:\(F_\mathcal{X}\leftarrow \mathcal{X}\times F_*\)
- 执行卷积操作:\(F_p\leftarrow Conv(K,F_\mathcal{X})\)
解决方案 - End - 对每个代表点周围的点特征做集成
通过上述方案,可以模拟CNN的特性,并且做到了开头\(\mathcal{X}-Conv\)的两件事。
问题
上面的\(\{p_{2,i}\}\)应该是有利于投影或聚集的点。在我们的实现中,在分类任务里面对\(\{p_{1,i}\}\)通过随即下采样得到\(\{p_{2,i}\}\),在分割任务里因为点的均匀性很重要所以这里使用最远点采样算法,文中给出假设应该是有更好的采样方案可以对分割任务进行优化,但是并没有做出探索。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号