霍夫线变换
这一节课将学到使用OpenCV的以下函数 HoughLines 和 HoughLinesP 来检测图像中的直线.和霍夫线变换的相关知识。
什么是霍夫线变换?
1.霍夫线变换是一种检测直线的算法。
2.在进行霍夫线变换之前必须对图像进行边缘检测处理,所以霍夫线变换的直接输入必须是边缘二值图像。
如何实现?
- 众所周知,一条直线在图像二维空间可由两个变量表示。例如:
a.在笛卡尔坐标系:可由参数斜率和截距表示。
b.在即坐标系:可由极径和极角表示。
2.对于霍夫变换,我们将用极坐标系来表示直线,因此,直线的表达式可以是:
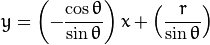
化简得: 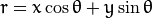
一般来说对于点(x0,y0),我们可以将通过这个点得一族直线统一定义为: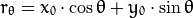
这就意味着对于每一对(rθ,θ)代表一条通过(x0,y0)的直线。
3.如果对于一个给定点(x0,y0)我们在极坐标对极径角平面绘出所有通过它的直线,将得到一条正弦曲线。例如,对于给定点x0=θ and y0=6 我们可以绘出下图(在平面)。
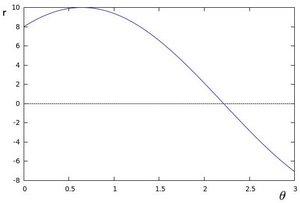 只绘制出满足下列条件的点r>0 and 0<θ<2∏
只绘制出满足下列条件的点r>0 and 0<θ<2∏
4.我们可以对图像中所有的点进行上述操作,如果两个不同点进行上述操作后得到的曲线在平面 θ-r 相交,则表示他们通过同一条直线。

三条曲线相交于(0.925,9.6),坐标表示的是参数对(θ,r),或者说是(x0,y0)和点(x1,y1)和点(x2,y2)。组成的平面内的直线。
5.说了这么都到底是想表达些什么呢?首先二值图像上面的点我们可以根据其取值不同来进行不同的分类,然后将这些点转化为极坐标点,极坐标点在极径极角平面可以画出所有通过他的直线, 我们将得到一条正弦曲线,我们可以根据这一特性来确定
在二值图像上那些亮度相近的点是一条直线上的。
6.这就是霍夫变换所做的。他追踪图像中每个点对应曲线间的交点,如果交与一点的曲线数量超过了某个阈值,那么就可以认为这个交点是图像中的一条直线。
OpenCV实现了两种霍夫变换:
a.标准霍夫变换
原理在上面的部分已经讲的差不多了,他能给我们提供一组参数对(θ,rθ)的集合来表示检测到的对象。早OpenCv中该变化使用HoughLines来实现
b.统计概率霍夫线变换
这是执行起来效率更高的霍夫线变换,他输出检测到的直线的端点(x0,y0,x1,y1)。在OpenCV中他通过函数HoughLinesP来实现。
代码
#include "opencv2/highgui/highgui.hpp" #include "opencv2/imgproc/imgproc.hpp" #include <iostream> using namespace cv; using namespace std; int main(int argc, char** argv) { const char* filename = "pic1.jpg"; Mat src = imread("res.jpg"); if(src.empty()) { cout << "can not open " << filename << endl; return -1; } Mat dst, cdst; Canny(src, dst, 50, 200, 3); cvtColor(dst, cdst, CV_GRAY2BGR); #if 0 vector<Vec2f> lines; HoughLines(dst, lines, 1, CV_PI/180, 100, 0, 0 ); for( size_t i = 0; i < lines.size(); i++ ) { float rho = lines[i][0], theta = lines[i][1]; Point pt1, pt2; double a = cos(theta), b = sin(theta); double x0 = a*rho, y0 = b*rho; pt1.x = cvRound(x0 + 1000*(-b)); pt1.y = cvRound(y0 + 1000*(a)); pt2.x = cvRound(x0 - 1000*(-b)); pt2.y = cvRound(y0 - 1000*(a)); line( cdst, pt1, pt2, Scalar(0,0,255), 3, CV_AA); } #else vector<Vec4i> lines; HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 ); for( size_t i = 0; i < lines.size(); i++ ) { Vec4i l = lines[i]; line( cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA); } #endif imshow("source", src); imshow("detected lines", cdst); waitKey(); return 0; }





