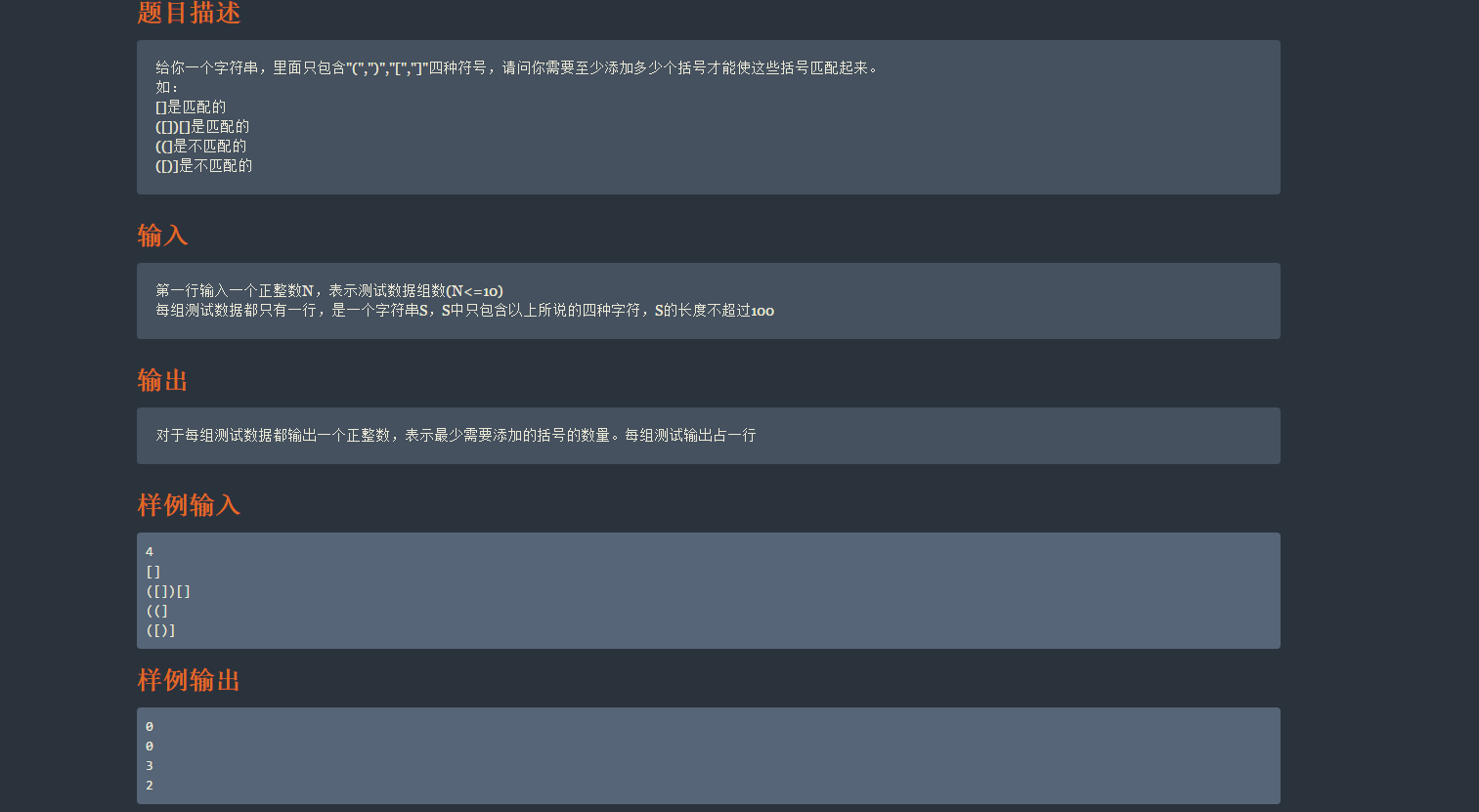
这里的括号匹配 , 如果两个相同的话 就执行下面的 语句
if(cmp(str[i],str[j]))
dp[i][j] = min(dp[i][j],dp[i+1][j-1]);
每次确定 从 i 到 j 的需要填补的 括号的时候 就默认 这个 值是 105
1 #include<stdio.h>
2 #include<string.h>
3 #include<math.h>
4 #include<iostream>
5 #include<limits.h>
6 #include<algorithm>
7 #include<queue>
8 #include<vector>
9 #include<set>
10 #include<stack>
11 #include<string>
12 #include<sstream>
13 #include<map>
14 #include<cctype>
15 using namespace std;
16 int dp[105][105];
17 bool cmp(int n,int m)
18 {
19 if((n == '('&&m == ')')||(n == '['&&m == ']'))
20 return true;
21 return false;
22 }
23 int main(void)
24 {
25 int n,m,i,j,k;
26 char str[101];
27 scanf("%d",&n);
28 while(n--)
29 {
30 scanf("%s",str);
31 int length = strlen(str);
32 memset(dp,0,sizeof(dp));
33 for(i = 0; i < length; i++)
34 dp[i][i] = 1;
35 for(m = 1; m < length; m++) // 先 让中间只相差一个数字 去计算一次
36 {
37 for(i = 0; i < length - m; i++)
38 {
39 j = i + m; // j 和 i 相差 m
40 dp[i][j] = 105; // 默认 i 和 j 之间需要105个 括号去 填充
41 if(cmp(str[i],str[j])) // 看看 i 和 j 是否配套
42 dp[i][j] = min(dp[i][j],dp[i+1][j-1]); // 配套的话 就从上次 和
43 for(k = i; k < j; k++)
44 {
45 dp[i][j] = min(dp[i][j],dp[i][k]+dp[k+1][j]);
46 }
47 }
48 }
49 printf("%d\n",dp[0][length-1]);
50 }
51 return 0;
52 }






