希尔排序 堆排序 归并排序

希尔排序(by Donald Shell):

//利用了插入排序的简单 ,同时克服 插入排序以此交换消去一个 逆序对的困难.

既然我们 决定 要 做上述之事   那么我们  最迫切的事情就是  确定我们以此交换 间隔几个位置?

假定给了一个需要排序的数组并且 按照5-间隔的方式进行排序　　附图如下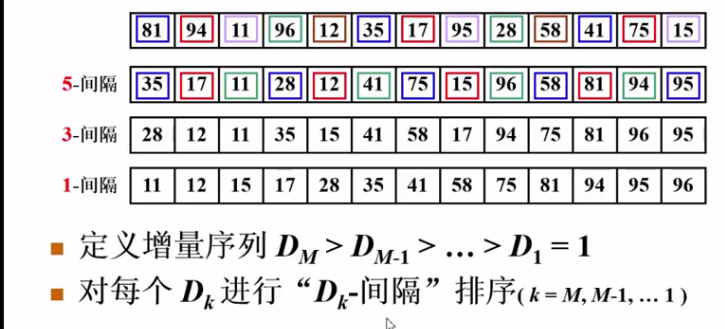

我们  慢慢的按照 越来越小的间隔开始去排序      (最后只能是间隔为1).

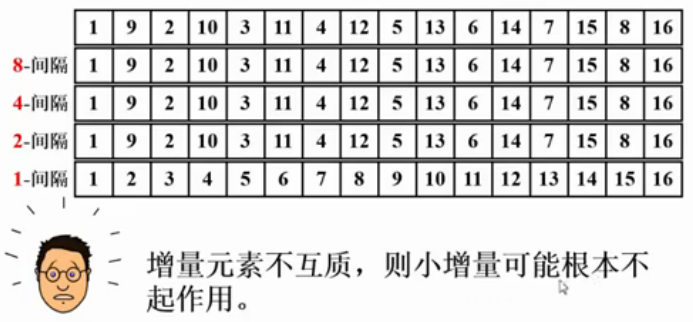
阿呆说  增量元素不互质  ,则最小增量可能根本不起作用    .会导致 很糟糕的时间复杂度,所以  会造成  N^2的时间复杂度 .(和插入排序一样.)   (讲插入排序的作用  目前就是 给希尔排序做铺垫.)

所以为了解决上述问题我们就引入一个Hibbard增量序列  Dk=2^k-1   相邻元素互质   最坏情况T=(N ^3/2)

 堆排序:

先回顾一下插入排序

 

void Selection_Sort ( ElementType A[], int N )
{ 
    for ( i = 0; i < N; i ++ )
    {
        MinPosition = ScanForMin( A, i, N–1 );     //对应的也是一个for循环 没有最好最坏情况.  
　　　　　//  所以一个  排序算法  的好坏就决定于上面的 寻找最小 数的 好坏
　　　　//所以我们如何找到最小元呢?  还是出去说吧.里面占地方.

        /*  从A[i] 到A[N–1] 中找最小元，并将其位置赋给MinPosition */
        Swap( A[i], A[MinPosition] );             //这里是n-1的时间复杂度  所以关键就在于上面的  寻找最小值
        /* 置 将未排序部分的最小元换到有序部分的最后位置 */
    }
}

 

 

 

雷迪森 按的 箭头们  有没有想到 堆排序?

如果这样做的话  我们就开启了一个堆排序....

 

void Heap_sort(Element A[],int n)
{
    BuildHeap(A);    // 有一个线性复杂度的方法可以直接将一个数组调整成一个最小堆
    for(i=0;i<N;i++)
    {
        TmpA[i]=deleteMin(A); 
    }
    for(i=0;i<N;i++)
    {   //还有一个比较坑的地方是  需要多开一个数组.而且
        A[i]=TmpA[i]; //赋值也需要浪费一点时间.  
    } 
}  //整体时间复杂度有 NlogN

 

 

 

下面 开始避免上面出现的问题.

我们可以将上述的最小堆调整成最大堆.     (附上一个堆排序的题目,和堆排序做出来的答案)

　//由于建初始堆所需的比较次数较多，所以堆排序不适宜于记录数较少的文件。
 1 void Heap_Sort(ElementType A[],int N)
{
    for(i=N/2;i>=0;i--) //  BuildHeap //建立一个最大堆.
        PercDown(A,i,N);
    for(i=N-1;i>0;i--)
    {
        Swap(&A[0],&A[i]);  //DeleteMax  
        PercDown(A,0,i);
    }
}
//  定理:堆排序处理N个不同元素的随机排列的平均次数是 2N log N - N log log N
//  虽然堆排序给出最佳平均时间复杂度 
,但实际效果不如用Sedgewick增量序列的希尔排序.

 

   开始归并排序吧.    对了再说一下    大家问一问 学长  java里面有指针没(指针只是一种思想. 只是 在上一个节点里面储存了,下一个节点的信息罢了.)

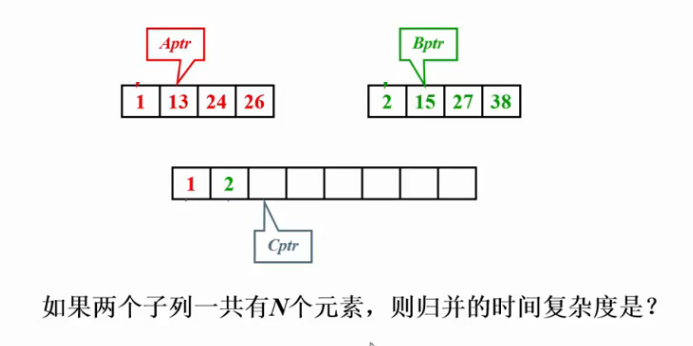
下面附上一个 

第一步 　　　　　　　　　　　　　这是将已经有序的 两个序列归并在一起.　

/* L =  左边起始位置, R =  右边起始位置, RightEnd = 置 右边终点位置 */
void Merge( ElementType A[], ElementType TmpA[],int L, int R, int RightEnd )
{ 
    LeftEnd = R - 1; /* 着 左边终点位置。假设左右两列挨着 */
    Tmp = L; /* 置 存放结果的数组的初始位置 */
    NumElements = RightEnd - L + 1;
    while( L <= LeftEnd && R <= RightEnd )     //      注意 代码中说的  L,R什么的是数组下标不是  地址 别想错
    {
        if ( A[L] <= A[R] ) 
            TmpA[Tmp++] = A[L++];
        else 
            TmpA[Tmp++] = A[R++];
    }
    while( L <= LeftEnd ) /* 的 直接复制左边剩下的 */
        TmpA[Tmp++] = A[L++];
    while( R <= RightEnd ) /*的 直接复制右边剩下的 */
        TmpA[Tmp++] = A[R++];
    for( i = 0; i < NumElements; i++, RightEnd -- )
        A[RightEnd] = TmpA[RightEnd];
}

第二步 下面是分而治之    

             这是  分而治之 讲一个很长的待排序列  划分为很小  递归的去解决  

void Msort(ElementType A[],ElementType TmpA[],int L,int RightEnd)
{
    int center;
    if(L<RightEnd)  //  带上纸和笔   理清递归.
    {
        center=(L+RightEnd)/2;
        Msort(A,TmpA,L,center);
        Msort(A,TmpA,center+1,RightEnd);
        Merge(A,TmpA,L,center+1,RightEnd);
    }
}

 

第三步   统一函数接口  

void Merge_sort(ElementType  A[],int N)
{
    ElementType *TmpA;
    TmpA=malloc(N*sizeof(ElementType));
    if(TmpA!=NULL)
    {
        MSort(A,TmpAm,0,N-1);
        free(TmpA);
    }
    else
        error ("空间不足\n");
}

 

----------话说递归都不是太好用---下面附上非递归算法----这才是重要的.--   下面附上  非递归算法的思想.

 

临时数组需要用多少容量(假设  待排序数组的容量为 N )----------答案有一种很大   就不说了

 

另一种就是开一个和 原先数组一样大的 , 数组去  解决问题.

void Merge_sort(ElementType  A[],int N)
{
    int length=1; //初始化自序列长度.
    ElementType *TmpA;  //声明一个林好似数组.
    TmpA=malloc(N*sizeof(ElementType));
    if(TmpA!=NULL)
    {
        while()
        {
            Merge_pass(A,TmpA,N,length);
            length=2*length;
            Mergth_pass(TmpA,A,N,length);
            length=2*length;
        }
        free(TmpA);
    }
    else
        error ("空间不足.\n");
}

 

归并排序 在  外排序时用的比较多   内排序时  没什么人用 .