----------拓扑排序--------------

拓扑排序

拓扑序:如果图中从V到W有一条有向路径,则V一定排在W之前.满足此条件的顶点序列称为一个拓扑序.

获得一个拓扑序的过程就是拓扑排序

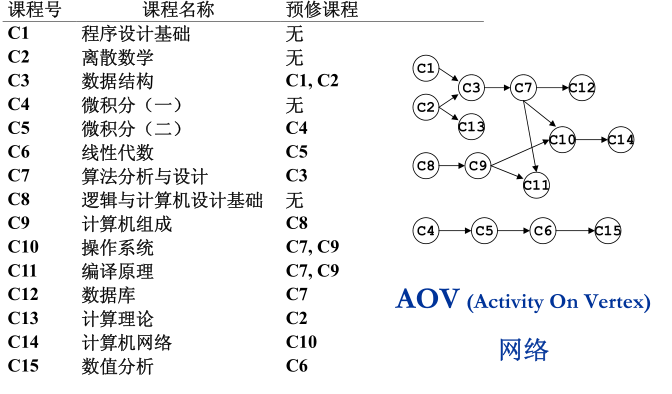
在进行拓扑排序之后会得到这样一个序列

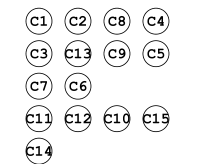
每一次我们要输出没有前驱顶点的结点,也就是没有入度的点.在输出之后就把这个顶点的出度设置为0

AOV(Activity On Vertex网络)如果有合理的拓扑序则必定是有向无环图(Directed Acyclic Graph , DAG)

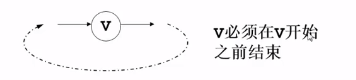
V必须在V开始之前结束,,,,明显错误,,,所以一个合理的拓扑序不可能存在环.

void TopSort()
{
    for(cnt=0;cnt<V;cnt++)
    {
        V=未输出的入度为0的顶点;    //下面 讨论这一步.
        if(这样的V不存在)
        {
            Error("图中有回路");
            break;
        }
        输出V,或者记录V的输出序号
        for(V的每个临接点W)
            Indegree[W]--;// 减少了V那么 V的每个临接点的入度都会减一.
    }
}

第一种解决方法是遍历一遍时间复杂度为 N^2 .

第二种解决方法是,随时将入度变为0的放到一个另外的容器里面.时间复杂度为常数级

第二种方法用队列的时候代码如下

void TopSort()
{
    for(途中的每个顶点V)
        if(Indegree[V]==0)
        Enqueue[V,Q];
    while(!IsEmpty(Q))
    {
        V=Dequeue(Q);
        输出V,或者记录V的输出序列号.
        for(V的每个临接点W)
        {
            if(--Indegree[W]==0)
                Enqueue[W,Q];
        }
    }
    if(输出的顶点不够顶点的个数)
        Error("图中有回路");
}