图的遍历---------开始开始-------o(∩_∩)o 哈哈
图的遍历
深度优先搜索(Depth First Search , DFS)
--深度优先搜索--我的理解就是分身术的另一种实现方法---用分身术将所有能看到的路都走一遍----这就是深度搜索---
下面给一个图 让大家理解一下
void DFS(Vertex V) //深度优先搜索的伪码描述 { visited[V]=ture; //先点亮这个节点的灯 for(V的每个临节点 W) //站在V的位置 所有能看到的灯 W if(!Visited[W])//如果没有亮 DFS(W);//走到这个灯的位置递归的点亮(递归确实很难理解,但是在前面我已经给了两个训练递归思想的代码,你还记得么?) } //不得不说 虽然递归十分耗费内存但是递归确实 很好用.
越看感觉越想 树的先序遍历,有木有? 递归的思想是一样的(你在树那里的遍历方法有几种这里可以用不?)
----------前面咱们说了两种----图的储存方式----
下面来说一下不同的储存方式 , 用于搜索带来的不同效果.
若有N个节点,E条边 , 时间复杂度是
· 用邻接矩阵储存图,有O(N+E) // 如果用邻接矩阵的话 在这个算法当中相当于 每个节点 每条边都走了一次.
· 用邻接矩阵储存图 , 有O(N^2) //这个怎么说呢 自己想想
void DFS(Vertex V) //深度优先搜索的伪码描述 { visited[V]=ture; //先点亮这个节点的灯 for(V的每个临节点 W) //站在V的位置 所有能看到的灯 W if(!Visited[W])//如果没有亮 DFS(W);//走到这个灯的位置递归的点亮(递归确实很难理解,但是在前面我已经给了两个训练递归思想的代码,你还记得么?) } //不得不说 虽然递归十分耗费内存但是递归确实 很好用.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------------今天听鹏哥说了一上午 也算复习 也算预习 也有收获 ------------
深度优先搜索,就是找一条线 向下面 一直搜 ,,,而广度优先搜索是 从一个点开始 向外面慢慢的扩散------
下面附上广搜的相关.
广度优先搜索(Breadth First Search ,,BFS)
从根节点出发,从上到下 ,从左到右-------具体的实现是借助一个队列---这个前面咱们将堆的时候好像说过.
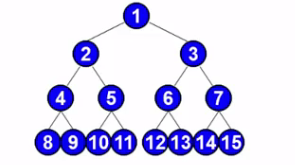走过的顺序就是这个
void BFS(Vertex V) //树的根节点 { visited[V]=ture; //访问 上面传下来的根节点 并且标记为已访问 Enqueue(V,Q); //将 V 压进队列里面 while(IsEmpty[Q]) //判断队列是否为空 { V=Dequeue(Q); //出队列 并且赋值给V for(V的每个临节点W) //V访问 V的每个临节点 { if(!visited[W]) //如果已经访问 就算了 否则进去, { visited[w]=ture; Enqueue(W,Q); //将刚才被删除的元素的 儿子压进去. } } } }
邻接矩阵 时间复杂度为 N^2 然而邻接表的时间复杂度是 N+E 思考一下 why?
-----------------------下面开始说 --两种不同的遍历 分别适用的方向.----下面附上一个 大侠走迷宫.-----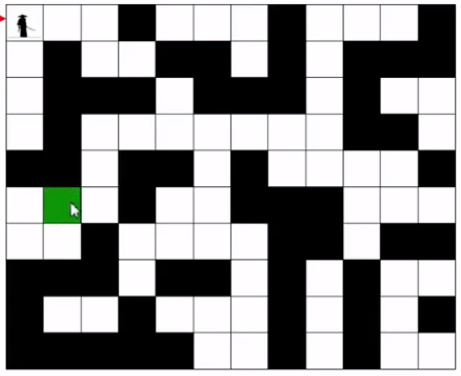
给大侠一点规定------大侠喜欢 从十二点方向开始,按照顺时针的方法走路口---------
这时候大侠走出迷宫的 所需要经过的 格子就很多了
如果大侠 按照广搜的方法 仍然 十二点顺时针 是什么情况?
-------------------------不挨着的节点怎么----图不连通?----那还遍历个什么呀?----------------------
连同: 如果从V到W存在一条(无向)路径,则称V和W是连通的.
路径:V到W的路径是一系列顶点{V,v1,v2,v3,...,vn,W}的集合其中任一一对相邻的顶点间都有图中的边.路径的长度是路径中的变数(如果带权的话,则是各边的权重之和) . 如果从V到W之间的所有顶点都不同则成为简单路径.
回路:起点等于终点的路径, (V ,v1,v2,v3,V 这就是一个回路).
连通图:图中任意两顶点均连通.
图不连通怎么办?
连通分量:无向图的极大连同子图 (好好理解慢慢看).
极大顶点数:再加一个顶点就不联通了.
极大边数:包含子图中所有顶点相连的所有边.
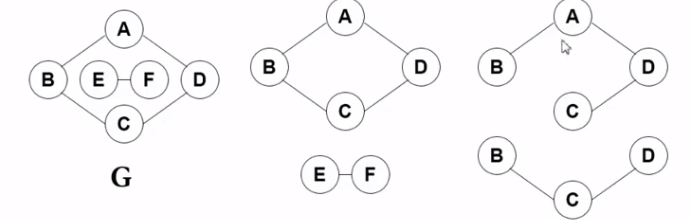
G是原图 后面的四个就是无向图G的极大连同子图 从上到下 从左到右的顺序开始说.
第一个 符合上述两点 第二个也符合
第三个 不符合第二点 第四个 不符合第一点
------------------------------------------------------------------------------------------------
下面说说 有向图 有向图分为强连同和弱连同
强连同:有向图中顶点V,W之间存在双向路径,则称V,和W是强连同的.(意思就是说 我也已从V 到W 也可以从W到V 其中不需要必须走同一条路)
强连通图:有向图中任意两顶点均强连同.
强连通分量:有向图的极大强连同子图.
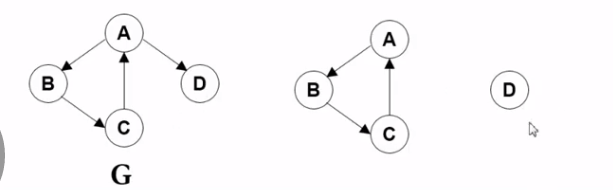
图G的极大强连同子图有两个 第一个 任意两点都可以连同 并且 再多一个 就不行了 第二个 也是
void DFS(Vertex V) //最终将所有连通的都 遍历了. { visited[V]=ture; for(V的每个节点W) if(!visited[w]) DFS(W); } /*不连通的怎么遍历呢?*/ void ListComponents(Graph G) { for(each V in G) //向下输送所有的 不连通分量 if(!visited[v]) { DFS(v); // or BFS[v]; } }
拯救007......007被 困在了一个孤岛上面 湖里面都是鳄鱼 英勇的零零七 决定一 鳄鱼头当成 跳板跳到河岸上面下面附图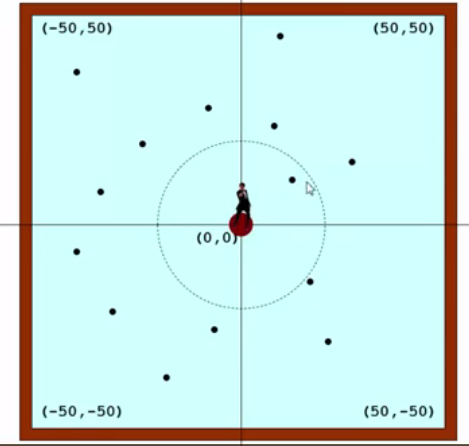
这一道题 深度优先 和广度优先 都可以 但是 根据实际问题来看 深度优先 可能更好一点.
我们在上面第一个程序上做一个 修改.
void Save007(Graph G) { for(each V in G) //孤岛上面的 所有相邻的 岛一个一个试 知道 跳出去. { if(!visited[V]&&FirstJumpe[V]) //没有跳过 并且 第一跳可以跳出. { answer=DFS[v]; } } if(answer==YEs) output("Yes"); else output("NO"); }
