-----二叉树的遍历-------
------------------先序遍历-----------------------
遍历过程:
①访问根节点。
②线序遍历其左子树。
③线序遍历其右子树。

/*这里的遍历顺序是 A B D F E C G H I*/
void PreOrderTraversal(BinTree BT) // { if(BT) //判断二叉树是否为空 { printf("%d",BT->Date); // 过了一个了 PreOderTraversal(BT->left); //递归调用了该函数。 检查左边。 PreOderTraversal(BT->right); } } //递归其实也像是一棵树,向下走当向下走不成的时候向上走一步,走另一个分支。
中序遍历,和后序遍历都是只是对。 那里的执行程序printf(“%d”,BT->Date);分别换到中间和 换到后面而已。
中序遍历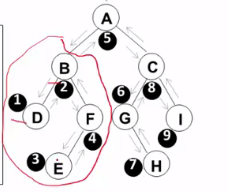 可以用这个锻炼递归的思路形成,D B E F E A C G H C I
可以用这个锻炼递归的思路形成,D B E F E A C G H C I
后序遍历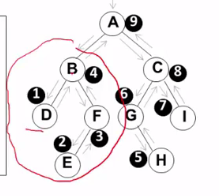 一个比一个难度高。。。。。。。
一个比一个难度高。。。。。。。
这三种便利方法不是太相同但是大部分是相同的。
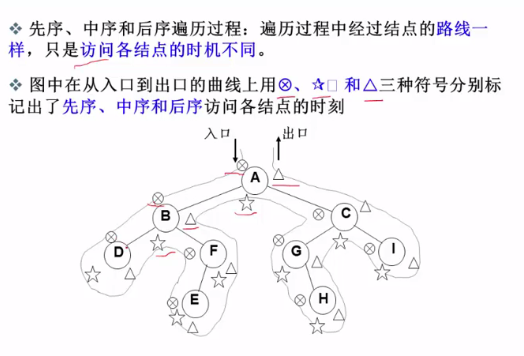
------------在这三种遍历的不同之中最能体会到 递归调用的实质-----
上面说了,树的三种遍历。但是都是递归的,在咱们刚刚开始的时候都说过了如果用递归的话,占用的内存太大。导致程序容易崩溃。刚好咱们前面学了 栈 所以应该就能想到 我们利用栈 将递归函数变成非递归函数。 Are you ready?
中序遍历。。。。。。。
void InOrderTraversal(BinTree BT) { BinTree T=BT; //创建一个临时变量 stack s=creatstack(MaxSize); //调用创建 堆栈的 函数 while(T||!IsEmpty) { while(T) //一直向左并且将沿途的 节点压入堆栈. { Push(S,T); T=T->Right; } if(!IsEmpty(s)) { T=Pop(s); //节点弹出堆栈 printf("%d",T->Date); //(访问)打印节点 T=T->Right; //转向右子树 } } }
下面附上先序。
/*只是将 标记的地方互换之后 就可以了。*/ void InOrderTraversal(BinTree BT) { BinTree T=BT; //创建一个临时变量 stack s=creatstack(MaxSize); //调用创建 堆栈的 函数 while(T||!IsEmpty) { while(T) //一直向左并且将沿途的 节点压入堆栈. { printf("%d",T->Date); //(访问)打印节点 ///******* T=T->Right; } if(!IsEmpty(s)) { T=Pop(s); //节点弹出堆栈 Push(S,T); //************** T=T->Right; //转向右子树 } } }
下面开始 二叉树的 层次遍历。
二叉树是一种二维结构,然而我们在遍历的时候就必须一个一个的去遍历,这样的话就需要每一个元素都有顺序,就需要把二位的结构变成一维的结构。这就是二叉树甚至多叉树进行遍历时需要处理的关键。
一层一层 一个一个 从上到下 从左到右,进行遍历。 首先从根节点开始将A放进去,然后抛出去A,然他的两个儿子进去,然后抛出B让她的两个儿子进去(first In first out) 然后 抛出去C然后让她的两个儿子进来。然后抛出去D,让他的两个儿子进来(发现没儿子,那就不用进来了。。。。。)就这样下去就遍历完了。
--颤抖吧---感受一下代码---哈哈----
/*层序基本过程:先从节点入队,然后:
① 从队列中取出一个元素; ②访问该元素所指的节点; ③若该元素所指的节点非空则按照从左到右的顺序放到队列中(FIFO)。 //层序遍历简单易懂(如果队列函数好些的话,以后就可以用测序遍历了。) void LevelOrderTraversal(BinTree BT) { Queue Q; BinTree T; if(!BT) //如果是空树的话直接返回 return ; AddQ(Q,BT); //将 根节点放到队列里面去。 while(!IsEmptyQ(Q)) //判断队列是否为空 { T=DeleteQ(Q); //从队列里面抛出去一个元素 printf("%d\n",T->Date); // 打印 所抛出去的元素。 if(T->Left) //如果有左儿子 AddQ(Q,T->Left); //左儿子进去 if(T->right) //如果有右儿子的话右儿子进去。 AddQ(Q,T->Right); } }





