PU-Net: Point Cloud Upsampling Network
测地距离和欧式距离
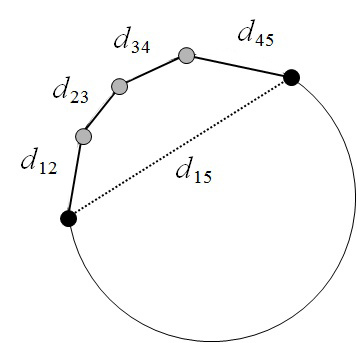
如图示欧氏距离为两点之间线段最短,所以欧氏距离为\(d_{15}\)。测地距离为实际上沿途最短距离为\(d_{12}+d_{23}+d_{34}+d_{45}\)
Earth Mover's Distance
EMD主要用于距离度量,度量两个分布之间的距离。此处的分布可以是点云。
在2D图像邻域,我们可以逐像素计算距离,从而去计算图像之间的距离,但是对于点云这种数据,应该怎么去度量距离呢?EMD就是常见的度量方式之一。
如果我们可以度量距离,我们就能够通过实现反向传播,来将两个点云之间的距离缩小/放大。可以将其用于点云的上采样、补全、重建等多种生成式任务当中,来实现形状的约束。
EMD
具体参考:https://zhuanlan.zhihu.com/p/145739750
2018 点云上采样开创性质文章
Abstract
- 数据驱动的上采样技术。
- 学习每个点的多级特征
- 在特征空间中通过多分支卷积单元去隐式的扩展点集
- 扩展后的特征被分为多个特征
- 重构为上采样的点集
本文提出数据驱动的点云上采样技术,主要思想是每个点学习多级特征(类似DGCNN),并通过特征空间中的多分支卷积单元隐式扩展点集。扩展后的特征被分割为多个特征,然后重构为上采样点集。我们的网络是应用在patch-level上的,它具有一个联合的损失函数,可以鼓励上采样的点保持在表面上的均匀分布。
此处使用了合成和扫描的数据进行了各种实现来评估我们的方法,并验证了其由于baseline方法和基于优化的方法。
Introduction
在本工作中,我们感兴趣的是一个上采样问题:给定一组采样点,通过学习训练数据集的几何形状,生成一组密集的点来描述底层的集合形状。这个上采样问题在本质上类似于图像的超分问题。
处理3D点而不是2D像素网格带来了新的挑战:
- 点云没有任何空间顺序和规则结构。
- 生成的点应该描述对象的底层集合问题,意味着生成的点应该大致位于目标对象表面。
- 生成的点应该是有信息的,不应该混杂在一起。
综上所述:生成的点数据点击在目标物体的表面应该更加均匀。因此输入点之间的简单插值并不能产生令人满意的效果。
为了解决这些问题,此处提出了点云的上采样网络,网络应用在Patch-level,具有一个联合损失函数,用于约束采样点保持在一个均匀分布的表面上。他的关键思想是每个点学习多级特征,然后通过特征空间中的多分支卷积单元隐式扩展点集。扩展后的特征被分割为多个特征,然后重构为上采样点集。
metrics
- 分布均匀性指标
- 距离表面偏差指标
此处制定了两个指标,分布均匀性和距离表面偏差,以定量评估上采样点集,并使用各种合成和真实扫描数据集测试我们的方法。我们还评估了我们的方法的性能,并将其与baseline和最先进的基于优化的方法进行比较。结果表明我们的上采样方法,均匀性和距离偏差最好。
相关工作
- optimization-based methods
Alexa等人的早期工作Computing and rendering point set surfaces.在PCL的MLS(Moving least Squares)用于表面平滑操作,该文章就是这个模块的理论基础。文章和模块解析具体参考此文。Lipman这些人提出了一种基于L1中值的局部最优投影算子,用于点的重采样和表面重建技术,这种方法及时在输入的点集包含噪声和异常值的时候也可以很好的工作。Huang等人提出了一种改进的加权LOP来解决点集密度问题。虽然这些工作已经证明了良好的结果,但是他们做了一个强有力的假设,即表面是光滑的,因此限制了方法的适用范围。然后Huang这些人引入了一种边缘感知的点集重采样方法,首先从边缘点开始重采样,然后逐步接近边缘和角,这些不够光滑的区域,但是他们的方法严重依赖于给定点发现的准确性和自习的参数调整。值得一提的是,Wu这些人提出了一种基于Deep point的表示方法,将点的巩固和完善融合在一个连贯的步骤当中,由于该方法的主要焦点是填充大空洞,但是不限制全局平滑,因此该方法对比较大的噪声很敏感,总的来说,上述方法不是数据驱动的,因此很大程度上依赖于先验知识。
- deep-learning-based methods
因为点云的特殊性,所以目前只有很少的作品采用深度学习模型直接处理点云。在本文之前没有专注于点云上采样的工作。
网络结构
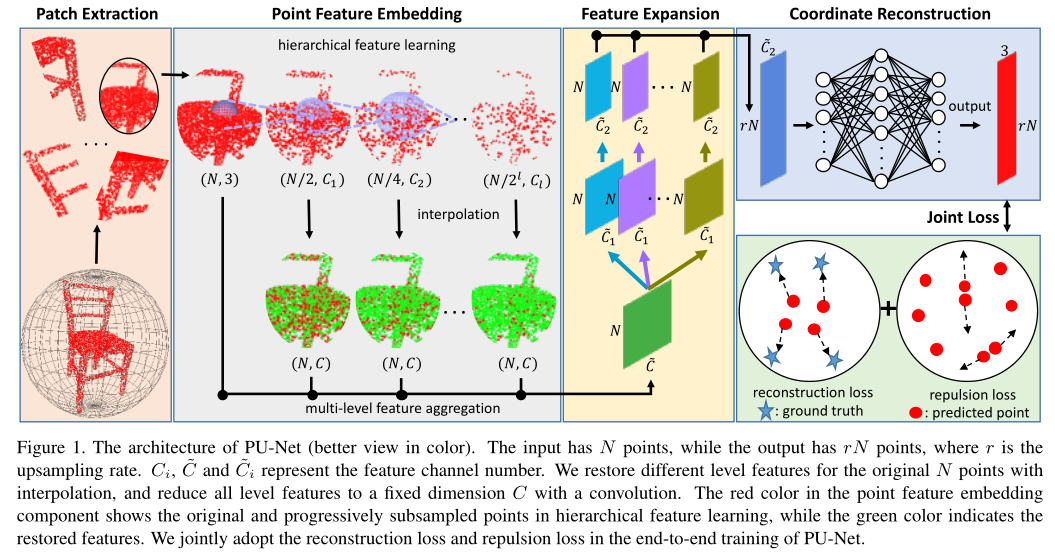
本文网络的体系结构由四个部分组成:Patch Extraction,Point Feature Embedding,Feature Expansion,Coordinate Reconstruction。
- 首先我们从给定的3D模型中提取不同尺度和不同分布的
patch Point Feature Embedding通过分层特征学习和多级特征聚合将原始三维坐标映射到特征空间中。- 我们使用
Feature Expansion扩展特征数量, - 在
Coordinate Reconstruction中通过一些列的全连接层去重建3D坐标作为输出点云。
Patch Extraction
我们使用一组3D对象作为训练的先验信息。这些物体涵盖了各种各样的形状,从光滑的表面到尖锐的棱角。从本质上说,我们的网络要对点云进行上采样,他应该学习对象的local geometry patterns,所以此时我们采用基于Patch的方法来训练网络并捕获集合语义。
做法:我们在这些对象的表面上随机选取M个点,对于每个点,我们都在他的表面上做一个Patch,这样一来Patch内的所有点,都和选定的点在一定的距离\(d\)内。然后我们使用泊松圆盘采样,去在每个Patch上(以centroid为中心,\(d\)为半径的圆,进行均匀泊松圆盘采样)随机的生成\(\hat{N}\)个点作为这个Patch上的参考标准分布。在上采样任务当中local和global上下文都有助于产生平滑和一致的输出。因此,我们将\(d\)设置为不同的大小,以便我们可以提取具有不同比例和密度的点。
Point Feature Embedding
为了从Patch中学习局部和全局几何上下文,我们考虑一下两种相辅相成的学习策略:
Hierarchical feature learning.分层次结构逐步捕获不断增长的特征,已经被证明是提取局部和全局特征的有效策略。其在PointNet++中也有使用,为了采用分层特征学习进行点云上采样,我们特别在每个级别中使用相对较小的分组半径\(d\),因为生成新点通常比中的高级识别任务涉及更多的本地上下文。
Multi-level feature aggregation.在网络中低层级的layer(Point Feature Embedding中靠左的图)通常对应较小尺度的特征集合结构更为精细。为了更好地上采样结果我们应该在不同级别上优化聚合特征。为了更好的上采样结果,我们应该在不同的级别上优化聚合特征。以前的一些工作采样跳过链接进行级联多级特征聚合如PointNet++,然而实验结果发现,在上采样问题中,使用类似DGCNN的多级特征聚合是很有效的(此处的interpolation个PointNet++的是一模一样的),因此选择使用DGCNN中的操作,让网络了解每个级别的重要性。
由于在分层特征提取中,每个面片上的输入点集,是要被二次采样的分层特征提取。我们通过PointNet++中的插值方法,首先从下采样点特征恢复所有原始点的特征,从而链接每个级别的点特征。具体而言,\(\ell\)层中插值点\(x\)的特征通过以下公式计算(此处的特征传播和PointNet++也是一样的。):
其中\(\omega_i(x)=\frac{1}{d(x,x_i)}\),这是一个反距离权重,\(x_i,x_2,x_3\)是\(\ell\)层中x的三个最近点。然后我们使用\(1\times 1\)的卷积将不同级别的插值特征减少到相同的维度,即\(C\)。最后我们将每个级别的特征连接起来作为嵌入点特征\(f\)。

Feature Expansion
在Point Feature Embedding之后,我们开始在特征空间中扩展特征的数量。这也相当于扩展点的数量,因为点和特征是可以相互转换的。假设在Point Feature Embedding得到的特征的维数是\(N\times\tilde{C}\),\(N\)为输入的点的数量,\(\tilde{C}\)是concatenated embedded特征的维数。Feature Expansion输出特征\(f'\)他的大小为\(rN\times\tilde{C}_2\),其中的\(r\)是上采样率,\(\tilde{C}_2\)是新的特征维度数。本质上它类似于图像相关任务中的上采样, 也可以通过反卷积或插值完成,然而由于点云的无规则性和无序性,这些操作对于点云而言是非常重要的。
因此我们提出了一种基于亚像素卷积层的有效特征扩展操作。这种操作可以被定义为。
其中\(\mathcal{C}_i^1(\cdot)\)和\(\mathcal{C}_i^2(\cdot)\)是两个独立的\(1\times 1\)的卷积,\(\mathcal{RS}(\cdot)\)是是一种reshape操作,用于将\(N\times r\tilde{C}_2\)的张量转化为\(rN\times\tilde{C}_2\)。我们强调嵌入空间中的特征已经通过有效的多级特征聚合封装了邻域点的相关空间信息,因此在执行此特征扩展操作时,我们不需要显式地考虑空间信息。
值得一提的是,由于集合中的第一个卷积\(\mathcal{C}_i^1(\cdot)\)生成的特征\(r\)具有高度的相似性,这将导致最终重建的3D点彼此过于靠近。因此,我们进一步为每个特征集添加另一个卷积(具有单独的权重)。由于我们训练网络学习r个特征集的r个不同卷积,这些新特征可以包含更多不同的信息,从而降低它们的相关性。 该特征扩展操作可通过对r特征集应用分离卷积来实现;见图1。它也可以通过计算效率更高的分组卷积来实现。
Coordinate Reconstruction
在这一部分中,我们从尺寸为\(rN\times\tilde{C}_2\)的Feature Expansion重建输出点的三维坐标。 具体来说,我们通过一系列完全连接的层对每个点的特征进行三维坐标回归,最终输出为上采样点坐标\(rN\times3\)。
End-to-End Network Training
Training Data Generation
上采样这个事情是ill-posed,因为上采样得到的点云本身就没有一个标准。具体而言就是给你一个稀疏的点云,可能有很多可行的上采样结果。因此是没有一个金标准的概念的。为了alleviate这个问题,我们提出了一种on-the-fly input generation scheme.
举例而言,训练用的Patch的参考GT的点分布是固定的,而每次的training epoch中输入的点是在GT点集中进行以\(r\)为采样率进行随机下采样的。直观的讲,对于给定的稀疏点云分布,这个方案相当于模拟许多可行的输出点云分布。此外这种操作也相当于进一步扩大训练集,使我们能够依赖相对较小的数据集进行训练。
Joint Loss Function
此处提出了一种新颖的联合损失函数去实现网络的端到端训练。就像前面讲到的一样,这个函数应该鼓励生成的点十分均匀的分布在对象的表面上。因此,我们设计了一个联合损失函数,它包含了reconstruction loss和repulsion loss。
Reconstruction loss. 为了在物体表面放置点,我们提出了使用Earth Mover's distance(EMD)作为我们的重建损失函数,以评估预测点云\(S_p\subseteq \mathbb{R}^3\)和GT点云\(S_{gt}\subseteq\mathcal{R}^3\)
其中\(\phi:S_p\rightarrow S_{gt}\)表示双射映射。实际上CD是评估两个点集之间相似性的另一个候选方案。然而和CD相比,EMD可以更好的捕捉形状,以估计输出点位于靠近底层对象去面的位置。因此我们选择在中间损失中使用EMD。
Repulsion loss:尽管重建损失可以再底层对象去面上生成点,但生成的点往往位于原始点附近,为了将生成的点更加均匀的分布,我们设计了斥点损失函数,其表示为:
其中\(\hat{N}=rN\)是输出点的数量,\(K(i)\)是点\(x_i\)的\(kNN\)索引集,\(||\cdot||\)是L2-norm。\(\eta(r)=-r\)被称为排斥项,这是一个递减函数,如果\(x_i\)太接近于\(K(i)\)中的其它点,则惩罚\(x_i\)。为了尽在\(x_i\)太接近其相邻点时惩罚\(x_i\),我们增加了两个限制:(1)我们只考虑距离\(x_i\)最近的\(kNN\)的点\(x_{i'}\)(2)我们在排斥损失中使用快速衰减权重函数\(\omega(r)\),\(\omega(r)=e^{-r^2/h^2}\)
最终我们使用如下联合损失函数,以端到端的方式训练网络:
其中的\(\theta\)表示网络中的参数,\(\alpha\)平衡重建损失和排斥损失,\(\beta\)表示权重衰减的乘数。为了简单起见,此处忽略每个训练样本的索引。
Experiments
Datasets
因为没有用于点云上采样的公共基准数据集,所以我们从Visionair中收集了60个不同的模型,从平滑的非刚性物体到棱角的刚性物体。在其中,我们随机选择40个去训练,剩下的去测试。我们为每个训练对象裁剪100个补丁,我们使用\(M=4000\)个补丁去训练整个网络。对于测试对象,我们使用蒙特卡罗随机抽样方法在每个对象上抽象5000个点作为输入。为了进一步证明模型的泛化能力,我们还直接在SHREC测试我们的网络,其包含来自50个类别的1200个形状。在细节上,考虑到每个类别中包含24个不同姿势的相似对象,我们从每个类别中随机选择一个模型用于测试。对于ModelNet40和ShapeNet,我们发现由于网格的质量比较低,所以很难从这些对象中提取片面。因此我们使用他们进行测试。
Implementation Details
每个面片的默认点数\(\hat{N}\)为4096,上采样率\(r\)为4。因此每个输入的patch有1024个点。为了避免过拟合此处使用随机旋转、移动和缩放来增加数据复杂性。我们在点特征嵌入组件中使用了4个级别,分组半径分别为0.05、0.1、0.2和0.3,恢复后的特征维数\(C\)为64.
斥点损失函数中的\(k\)和\(h\)被设置为5和0.03。权重平衡参数\(\alpha\)和\(\beta\)被设置为\(0.01\)和\(10^{-5}\)
Evaluation Metric
为了定量评估输出点集的质量,我们制定了两个度量标准来度量输出点和标准网格之间的偏差,以及输出点的分布均匀性。对于曲面偏差,我们为每个预测点\(x_i\)找到网格上最近的\(\hat{x}_i\)并计算他们之间的距离。然后我们计算所有点的平均值和标准偏差,作为我们的指标之一。
至于均匀性度量,我们在物体表面随机放置了\(D\)个相等大小的圆盘(在此处的实验中,\(D=9000\)),并计算圆盘内点数的标准偏差。我们进一步规范化计算每个对象的密度,然后计算测试数据集中所有对象的整体一致性。因此,我们将标准化均匀系数和磁盘面积百分比\(p\)定义为:
其中\(n^k_i\)是第\(k\)个物体的第\(i\)个圆盘内点的个数,\(N^k\)是第\(k\)个物体上点数总数,\(k\)是测试物体的总数,\(p\)是圆盘面积占物体总面积的百分比。




