SampleNet: Differentiable Point Cloud Sampling

Abstract

• 经典的采样方法（FPS）之类的没有考虑到下游任务。
• 改组上一篇工作没有解决不可微性，而是提供了变通的方法。
• 本文提出了解决不可微性的方法
• 可微松弛点云采样，近似采样点作为一个混合点在主要输入点云。

Introduction

FPS是任务无关的，它最小化了集合误差，并且不考虑采样点云的后续处理。

Learning to Sample提出了一种根据任务的抽样方法，他们的主要想法是简化点云，然后对点云进行采样。但是这个采样得到的集合不能保证是输入的子集。因此，在后处理步骤中，他们将每个简化点与输入点云中最近的相邻点进行匹配从而得到子集。

简化的点云必须平衡两个相互冲突的条件：

1. 简化的点云需要和原始点云保持形状的相似性
2. 简化的点云对于后续的任务有优化效果

此文扩展了Learning to Sample的工作，在训练过程中，通过匹配步骤引入一个可微的松弛（如最近邻选择，下图2），这种我们称之为软投影的操作，用输入中最近邻的甲醛平均替代采样集合中的每个点。在训练过程中，对权值进行优化以逼近最近邻的选择，并在推理阶段完成。

软投影操作方式改变了表示方式，这些投影点不是在自由空间中的绝对坐标，而是用他们在初始点云中的局部邻域的权值坐标来表示。这个操作由temperature参数控制，他在训练过程中被最小化，以创建一个模拟退火计划。

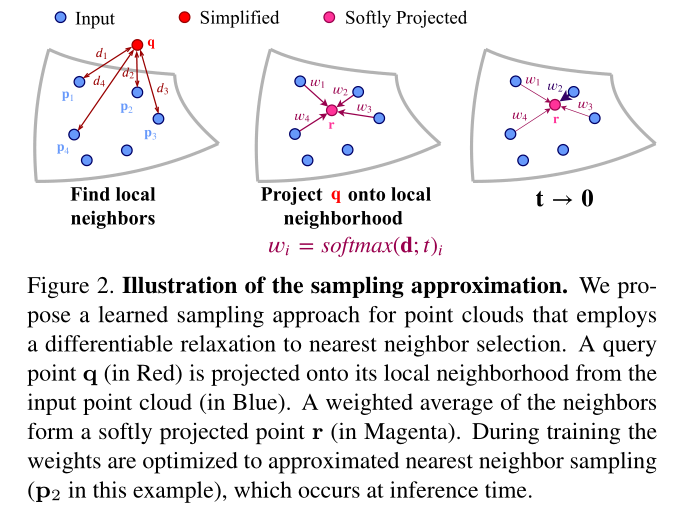
本文贡献：

1. 一种新颖的点云采样可微近似的方法
2. 和非学习以及学习的方法相比，使用点云采样进行分类和重建任务的性能得到了改善
3. 采用该方法进行点云配准

Related Work

此处是需要读一下参考文献

Nearest neighbor selection最近邻方法在文献中被广泛应用于信息融合。在神经网络的背景下，使用最近邻的一个显著缺点是，选择的规则是不可微的，Goldberger 等人提出了最近邻规则的随机松弛。他们在候选邻居集合上定义了一个分类分布，其中1-NN规则是改分布的极限情况。

后来Plotz and Roth通过提出k近邻选择规则的确定性松弛推广了Goldberger的工作。他们提出了一种神经网络层，称为神经最邻近块，它利用了KNN
松弛。在该层中。利用特征空间中邻居的加权平均进行信息传播。相邻权值用控制权值分布均匀性的温度系数进行缩放。在我们的工作中使用放松最近邻选择作为一种近似点云采样的方法。而在Plotz and Roth的工作中，温度系数是不受约束的，我们在训练过程中提升一个小的温度值，来近似最近邻的选择。

最近又提出了另一种子抽样的方法，将特征最活跃的点传递到下一网络层

Learning to Sample提出了一种面向学习任务的点云采样的方法，但是实现方法导致了训练阶段和推理阶段之间的性能差距，此处我们在训练过程中通过一个可微的最近邻近似来减轻这个问题。

Method

图3描述了我们的抽样方法SampleNet的概述。首先，在n个点的完整点云上对任务网络进行预训练并固定参数。然后，SampleNet取一个完整的输入P，通过神经网络将其简化为一个更小有m个点的集合Q。Q是通过最近邻选择的可微松弛软投影到P上的。最终将SampleNet的输出R，喂到任务网络当中。

1. 首先使用有\(n\)个点的完整点云对任务网络进行预训练并固定参数
2. 然后SampleNet吃进去完整的点云\(P\)，并且通过神经网络将其简化为只有\(m\)个点的集合Q
3. Q是通过最近邻选择的可微松弛软投影到P上的
4. SampleNet输出点集R作为TaskNet的输入

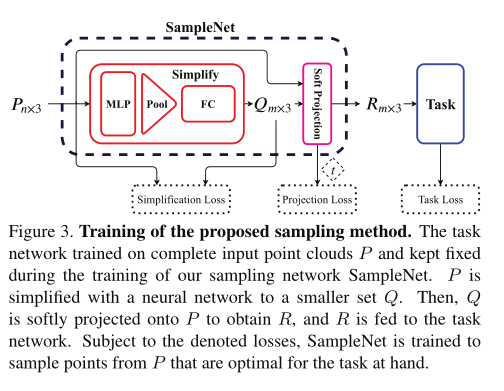
SampleNet用一下三个损失函数进行训练：

\[\mathcal{L}^{samp}_{total}=\mathcal{L}_{task}(R)+\alpha\mathcal{L}_{simplify}(Q,P)+\lambda\mathcal{L}_{project}\tag{1} \]

其中第一项\(\mathcal{L}_{task}(R)\)用于优化任务的采样集合，他的目的是保持保持采样点云的任务性能。\(\mathcal{L}_{simplify}(Q,P)\)让采样集合尽量接近输入集合的形状。也就是说Q中的每个点在P中都有一个闭合点，反之亦然。最后一项，\(\mathcal{L}_{project}\)通过软投影运算，对输入点云中的点进行近似采样。

Learning to Sample的前置知识

给定一个有\(n\)个点的3D坐标点云\(P\in\mathbb{R}^{n\times 3}\)，目标是找到一个有\(m\)个点的子集\(R^*\in\mathbb{R}^{m\times 3}\)，使采样的点云\(R^*\)是针对目标任务\(T\)有过优化的。将\(T\)的目标函数表示为\(\mathcal{F}\)，则\(R^*\)由下：

\[R^*=arg\min_R \mathcal{F}(T(R)), R\subset P, |R|=m\leq n.\tag{2} \]

• 限制抽样出来的子集对下游任务是有优化效果的

由于抽样问题的不可微性，从而就有一个挑战性问题。提出了一种由\(P\)生成\(Q\)的网络，它主要有以下两种性质：其中\(Q\)是问题的最优解，其点接近于\(P\)的点。并且由于损失函数的约束（如Learning to Sample），生成的Q的集合中的点比较接近原始输入P集合中的点位置。为了鼓励点之间的距离尽量接近此处提出一个损失函数用于约束：

\[\mathcal{L}_a(X,Y)=\frac{1}{|X|}\sum_{x\in X}\min_{y\in Y}||x-y||^2_2\tag{3} \]

最大近邻损失为：

\[\mathcal{L}_m(X,Y)=\max_{x\in X}\min_{y\in Y}||x-y||_2^2\tag{4} \]

\(P\)是输入，\(Q\)是输出，\(R\)是喂到任务网络的输入。综上所述，Simplification Loss为：

\[\mathcal{L}_{simplify}(Q,P)=\mathcal{L}_a(Q,P)+\beta\mathcal{L}_m(Q,P)+(\gamma+\delta|Q|)\mathcal{L}_a(P,Q)\tag{5} \]

• \(\mathcal{L}_a(Q,P)\) 让生成点尽量和原始输入点重合
• \(\mathcal{L}_a(P,Q)\) 约束生成点的形状尽量和输入点的形状相似
• \(\mathcal{L}_m(Q,P)\) 最差情况下生成点距离原始点的最大距离。

为了针对任务优化点集Q，我们将任务损失添加到优化目标当中，所以Simplification network的损失为：

\[\mathcal{L}_s(Q,P)=\mathcal{L}_{task}(Q)+\alpha\mathcal{L}_{simplify}(Q,P)\tag{6} \]

上面的采样网络是针对采样大小为m进行训练的。Learning to Sample提出了一种针对可变采样大小的网络，针对任务对点的关键性进行排序，并且可以输出任意大小的采样样本。

\[\mathcal{L}_{prog}(Q,P)=\sum_{c\in C_s}\mathcal{L}_s(Q_c,P)\tag{7} \]

其中的\(Q_c\)的大小是可以控制的。

对于前人工作的扩展

此处没有像之前一样针对简化之后的点云进行匹配从而得到采样的点，反而使用软投影操作。该操作如图4所示，\(q\in Q\)中的每个点\(q\)被软投影到他的邻域当中，这里的邻域指的是他在原始完整点云中\(P\)的\(k\)个最近邻的邻域定义，从而得到一个投影点\(r\in R\)。点\(r\)是原始点\(P\)的加权平均：

\[r=\sum_{i\in\mathcal{N}_P(q)}\omega_i P_i\tag{8} \]

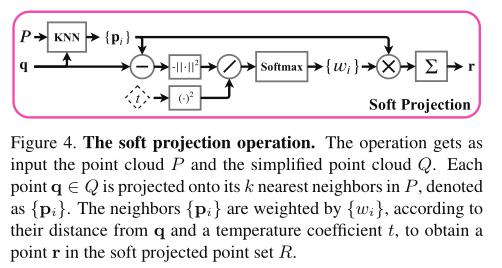
其中\(\mathcal{N}_P(q)\)包含\(P\)中与\(q\)最邻近的\(k\)个坐标，其中的权重\(\{\omega_i\}\)是根据\(q\)和与其邻居之间的距离确定的，用一个可学习的温度系数\(t\)确定。

\[\omega_i=\frac{e^{-d^2_i/t^2}}{\sum_{j\in \mathcal{N}_P(q)}e^{-d^2_j/t^2}}\tag{9} \]

其中的距离函数为\(d_i=||q-P_i||_2\)
邻域的大小\(k=|\mathcal{N}_P(q)|\)在采样中也扮演了一个重要的角色，通过距离项，网络可以对简化后的点进行调整，使其逼近局部区域内的不同输入点。虽然小的局部邻域大小可以降低探索区域，但是过大的大小也会 造成局部上下文的信息损失。

权值\(\{\omega_i\}\)可以看作是点\(\{P_i\}\)上的概率分布，其中\(r\)为期望值。温度系数控制着这种分布的形状。在\(t→0\)的极限下，分布收敛于一个位于最近邻点的克罗内克函数。考虑到这些观察结果，我们希望点r从P的局部邻域近似采样。为了实现这一点，我们添加了一个投影损失，如下所示:

\[\mathcal{L}_{project}=t^2\tag{10} \]

该损失函数使\(t\)值尽量地小。

在这种采样方法中，任务网络喂进去的使投影的点集\(R\)而不是简化的集合\(q\)来输入的。因为\(R\)中的每一个点都从\(P\)中估计选择了一个点，所以我们的网络使采样输入点云而不是简化输入点云。我们的采样方法也可以很容易的扩展到可变采样大小的网络中，此时的损失函数的形式为：

\[\mathcal{L}_{total}^{prog}=\sum_{c\in C_s}(\mathcal{L}_{task}(R_c)+\alpha\mathcal{L_{simplify}(Q_c,P)})+\lambda\mathcal{L}_{project}\tag{11} \]

其中\(R_c\)为对\(Q_c\)进行软投影运算得到的点集。在推理阶段，我们使用采样替代软投影，以获得一个采样点云\(R^*\)。就像在分类问题中，对于每个点\(r^*\in R^*\)，我们选择具有最高投影权值的点\(P_i\)：

\[r^*\in P_i*, i^*=arg\max_{i\in \mathcal{N}P(q)}\omega_i\tag{12} \]

和Learning to Sample类似，如果多个点\(r^*\)对应同一个点\(P_i*\)，我们去唯一的采样点集，使用最多m点的FPS完成它，并评估任务性能。

软投影作为幂等运算，严格的讲软投影（公式8）不是幂等运算，因此不构成数学投影。然而当方程9中的温度系数趋近于0的时候，得到幂等抽样运算。

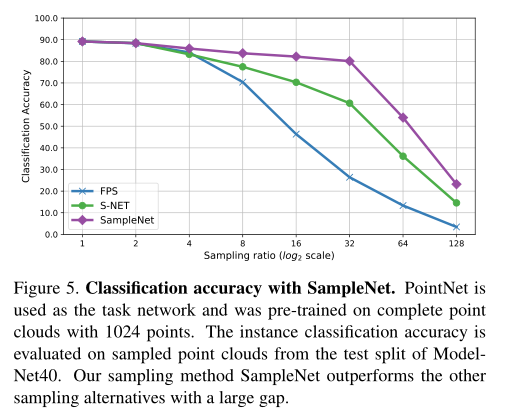
Result