Learning to Sample

Abstract

处理大型的点云是一项很有挑战性的任务，因此，我们将点云采样到一个合适的size去更方便的处理。

• 目前流行的采样方法是FPS，但是FPS对于下游任务是不可知的，如在反向传播啥的，他们之间是没有交互的。
• 我们证明了通过dl去学习如何采样是更好的，因此提出了一个深度网络来简化三维点云。其被称为S-NET。
• 该方法可以解决第一点，也就是针对特定任务进行优化。

Introduction

• FPS等这些方法考虑了点云的结构，选取一组彼此相距最远的点。
• 这些采样方法和文献中其他方法一样，都是根据非学习的预定规则进行操作的。
• S-NET学习生成更小的点云，该点云采样可以为下游任务进行针对性优化。

简化之后的点云必须平衡两个相互冲突的方面：

• 希望它保持和原始形状的相似性，
• 希望他可以优化到后续任务。
  我们通过训练网络生成一组满足两个目标的点来解决这个问题：采样损失和任务损失。
• 采样损失驱动生成的点的形状接近输入点云。
• 任务损失确保点对任务有优化。

FPS的一个优点是他采样得到的集合是原始点的子集，但是S-NET生成的简化点云并不能保证是输入点云的子集。

• 这个方法可以被视为是一种特征选择机制，每个点都是基础形状的一个特征，此处试图找出对任务贡献最大的点。
• 它也可以被解释为是视觉注意力的一种形式，将后续的任务网络集中在重要的点上。

贡献：

• 针对特定任务数据驱动采样方法
• 一种递进的抽样方法，根据点与任务的相关性进行排序

相关工作

点云的采样和简化

相关的方法，都是在优化各种抽样目标，然而他们没有考虑到所执行的任务的目标。

Method

问题描述：给定一个点集\(P=\{p_i\in\mathbb{R}^3,i=1,\dots,n\}\)，采样大小为\(k\leq n\)和一个任务网络\(T\)，找出\(k\)个点的子集\(S^*\)，使任务网络的目标函数\(f\)最小化。

\[S^*=argmin_S f(T(S)),S\subset P,|S|=k\leq n\tag{1} \]

\(\color{red}{这个问题带来了一个挑战就是采样看起来类似于池化，但是采样是无法反向传播的，但是池化可以，因此可以计算池化的梯度。}\)

然而离散采样就像arg-pooling，传播的值不能增量的更新。因此抽样操作不可以直接进行训练。因此，我们将生成的点和原始点云进行匹配，得到输入点的子集，即采样点。如下图

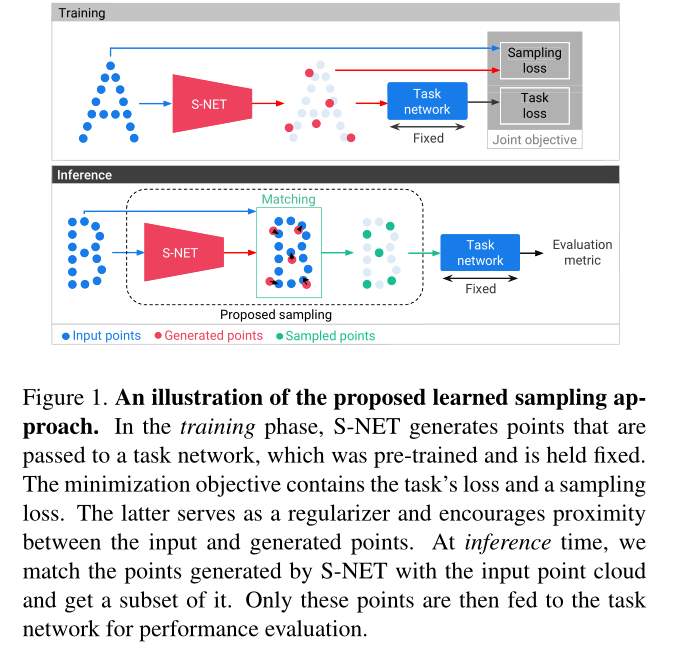
S-NET的输入是\(n\)个三维坐标的集合，代表一个三维形状。S-NET的输出是\(k\)个生成的点。S-NET后面是一个任务网络。输入\(n\)个点对任务网络进行预训练，在点云上执行给定的任务。S-NET在训练和测试的过程中保持固定，这确保了采样是针对任务进行优化的，而不是针对任意抽样进行优化的任务。

---

在训练阶段，生成的点被送到任务网络当中，这些点通过最小化任务损失来优化手头的任务。并且使用第二个损失项，鼓励生成的每个点靠近输入点的位置，并迫使生成的点在输入点云的分布中扩散。

---

在推理阶段的时候，将生成的点和输入点云进行匹配以获得其子集。这些采样点就是我们的最终输出采样点，这些点通过网络并对其性能进行评估。

此处提供了两个采样版本：S-NET和ProgressiveNet。在第一个版本中，我们根据样本大小训练不同的采样网络。在第二个版本中，它可以产生任何大小的 小于输入样本的采样样本。

S-NET

S-NET的结构使用的是PointNet的方法。输入点经过一组\(1\times 1\)的卷积层，得到每个点的特征向量。然后使用对称的特征最大池来获得全局特征向量。最后，我们使用几个完全连接的层，最后一层的输出是生成的点集。

我们将生成的点集表示为\(G\)，输入的点集表示为\(P\)，我们构造一个采样正则化损失，它由三个项组成：

\[L_f(G,P)=\frac{1}{|G|}\sum_{g\in G}\min_{p\in P}||g-p||_2^2\tag{2} \]

\[L_m(G,P)=\max_{g\in G}\min_{p\in P}||g-p||^2_2\tag{3} \]

\[L_b(G,P)=\frac{1}{|P|}\sum_{p\in P}\min_{g\in G}||p-g||_2^2\tag{4} \]

\(L_f\)和\(L_m\)在平均和最差的情况下，让\(G\)尽量可能的接近\(P\)。\(L_b\)保证生成的点尽量均匀的分布在输入点上。我们可以将上述公式转化为:

\[L_s(G,P)=L_f(G,P)+\beta L_m(G,P)+(\gamma+\delta|G|)L_b(G,P)\tag{5} \]

此外我们使用\(L_{task}\)表示任务网络损失，最终S-NET的损失函数为：

\[L^{S-NET}(G,P)=L_{task}(G)+\alpha L_s(G,P)\tag{6} \]

S-NET的输出是\(k \times 3\)的矩阵，\(k\)是采样样本的点数，接下来我们就对这\(k\)个点进行训练。

Matching

生成的点G不能保证是输入点\(P\)的子集，为了得到输入点的子集，我们将生成的点匹配到输入点云。

一个广泛使用的匹配两个点集的方法是EMD，它可以在集合之间找到一个bijection，使对应的点的距离最小，但是它要求这两个点集有相同的数量。但是在这里我们的两个点集的大小是不同的。

我们测试两种匹配方法。第一种方法是将EMD适用于不均匀点集。第二种是基于最近邻匹配的问题。这里我们使用的是第二种，它可以产生更好的效果。在基于最近邻的匹配中，每个点\(x\in G\)被替代为欧几里得空间内最近的点\(y^*\in P\):

\[y^*=arg\min_{y\in P}||x-y||_2\tag{7} \]

由于\(G\)中的几个点可能会接近于\(P\)中的同一个点，所以采样点的数量可能会小于需要点的数量。因此我们去掉重复的点并且得到一个初始的采样集合。然后我们通过FPS完成这个集合，我们每一步都从P中添加一个距离当前点集最远的点

匹配过程我们仅仅在推理时使用，作为推理的最后一步。在训练阶段当中，生成的点由任务网络按照原样处理，因为匹配是不可微的，不能将任务损失传播回S-NET

ProgressiveNet: sampling as ordering

S-NET被训练来采样单一，预训练过的尺寸大小的点。但是如果我们需要很多个采样大小呢？那么就需要对应数量的S-NET被训练。如果我们想训练一个可以产出任意大小的采样算法要怎么做的，然后这里提出了ProgressiveNet。ProgressiveNet的训练输入是给定大小的点云，输出是同样大小的点云，虽然输入点的顺序是任意的，但是输出点的顺序是根据他们与任务的相关性排序的。这样就允许我们对任意大小的样本进行抽样，我们只需要获取ProgressiveNet输出的前\(k\)个点云，然后丢弃其他样本。ProgressiveNet的结构和S-NET的相同，最后一个全连接层的大小等于输入点云的大小。

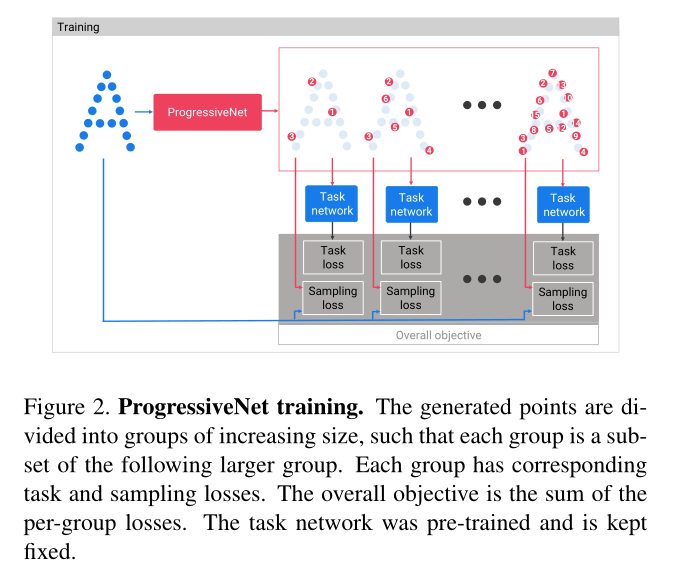
为了训练ProgressiveNet我们定义一个集合\(C_s=\{2^1,2^2,\dots,2^{log_2(n)}\}\)。对于每一个大小\(c\in C_s\)我们计算任务损失项和一个采样正则化损失项，使ProgressiveNet的总损失变为：

\[L^{ProgressiveNet}(G,P)=\sum_{c\in C_s}L^{S-NET}(G_c,P)\tag{8} \]

其中的\(L^{S-NET}\)是方程6定义的公式，\(G_c\)是ProgressiveNet生成的点的前\(c\)个点

不继续看了， 这个没啥东西。 就是为了可变采样大小，通过给采样点排序的方法。

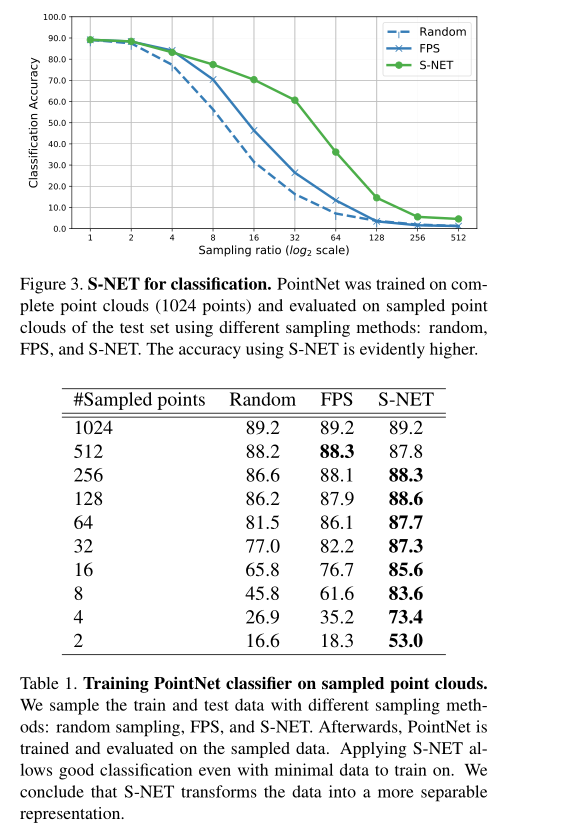
实验