采样算法

Farthest_Point_Sample算法本身是比较简单的，大概意思如下：

• 初始化一个distance意义是距离当前点集，每个点的距离
• 首选随机从点集中选择一个点出来，作为已选点集的第一个点
• 然后做其余点和他之间的差，放入distance
• 从中选择一个最远的点，放入已选点集合，然后重复计算更新距离distance距离当前点集的距离。

做到尽量均匀的采样，每次都找距离当前已收录点集的最远点加入点集。

Farthest_Point_Sample

```python def farthest_point_sample(point, npoint): N, D = point.shape xyz = point[:, :3] centroids = np.zeros((npoint,)) distance = np.ones((N,)) * 1e10 farthest = np.random.randint(0, N) for i in range(npoint): centroids[i] = farthest centroid = xyz[farthest, :] dist = np.sum(np.array((xyz - centroid)) ** 2, -1) mask = dist < distance distance[mask] = dist[mask] farthest = np.argmax(distance, -1) point = point[centroids.astype(np.int32)] return point ```

---

Poisson_Disk_Sampling：貌似挺麻烦的，大概生成的东西是，点和点之间的间距比较平均，不会靠的特别近， 也是属于平均的采样。

PDS

第一步：设定好两个点之间最近的距离r，以及采样点所在空间的维度n，比如2维平面
	
第二步：在空间里生成足够多的网格，保证不接触的两个网格之间的点的距离大于r，并且网格数量足够多保证每个网格至多只需装一个采样点就能满足采样数量。为了最优化，一般取网格边长为 $\frac{r}{\sqrt{n}}$（等腰三角形边长） 。
	
第三步：随机生成一个点，再创建两个数组，第一个是处理数组，第二个是结果数组，即最终的输出数组。把这个点放进处理数组中和结果数组中。
	
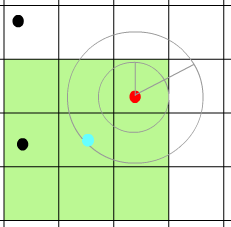
第四步：如果处理数组非空，从中随机选择一个点，如下图的红点，并把这个点从处理数组中删除。如果处理数组是空的，直接输出结果数组并结束算法。
	
第五步：设定最小距离minr，比如r，最大距离maxr，比如2*r。以红点为中心生成一个圆环，如下图灰色圆环，在这个圆环中生成一个采样点，如下图蓝点。
	
第六步：检测这个蓝点是否与其他点隔得太近，也就是距离小于r，由于之前已经设定好了网格，所以这里只要检查9个网格里的点就行了。如上图浅蓝色点周围的绿色的网格。隔得太近的就取消这个蓝点，否则就保留并放入处理数组和结果数组中。
	
第七步：设定好采样次数k，比如30。如果经过k次采样后，在圆环里仍然找不到可用的新点，那么就放弃这次采样。然后重复第三步。

网上流传的大多是这个说法，但是在看到的时候，我也产生了类似的疑问：

后来想了一下，大概应该是这样的，然后在下面做出了回答：

---

Gumbel-Subset-Sampling