Relation-Shape Convolutional Neural Network for Point Cloud Analysis

来源 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).

点云主要挑战：

  1. \(P\)是无序的，因此需要学习的东西是置换不变的；
  2. \(P\)分布在三维几何空间中，因此要求学习的模型应该对其刚性变换（旋转和平移）有鲁棒性；
  3. \(P\)形成一个潜在的形状，因此学习到的表征是应该可以判别形状的

以PointCNN中的\(\mathcal{X}-Conv\)为例，此处做个引子带出来卷积的方法。
\(\mathcal{X}-Conv\)来鹅城只为两件事：

  • 对每个代表点周围的点特征做集成。
  • 在隐空间对输入做重排去除输入顺序的影响。

Abstract

点云分析是一件很有挑战性的事情，因为不规则点中隐含的形状很难捕捉。在本文中提出了RS-CNN，即关系形状卷积神经网络，他将规则网格CNN扩展到不规则结构中，用于点云分析。RS-CNN的关键是从关系中学习，例如点之间的几何拓扑约束。具体地说，局部点集的卷积权重在该点集中的某个样例点和其他点之间在预定义的几何关系中学习高等级的关系表达。通过这种办法，可以获得关于该点的空间布局，局部表征和显式推理。RS-CNN利用这种卷积作为基本算子，可以开发出一种层次化的结构，以实现下上下文的形状感知学习。

  • 卷积权重学习central point关于other point的几何拓扑约束，通过预定义的几何关系，学习这个先验的形状表达
  • 实现层次化的结构，以扩大感受野

Introduction

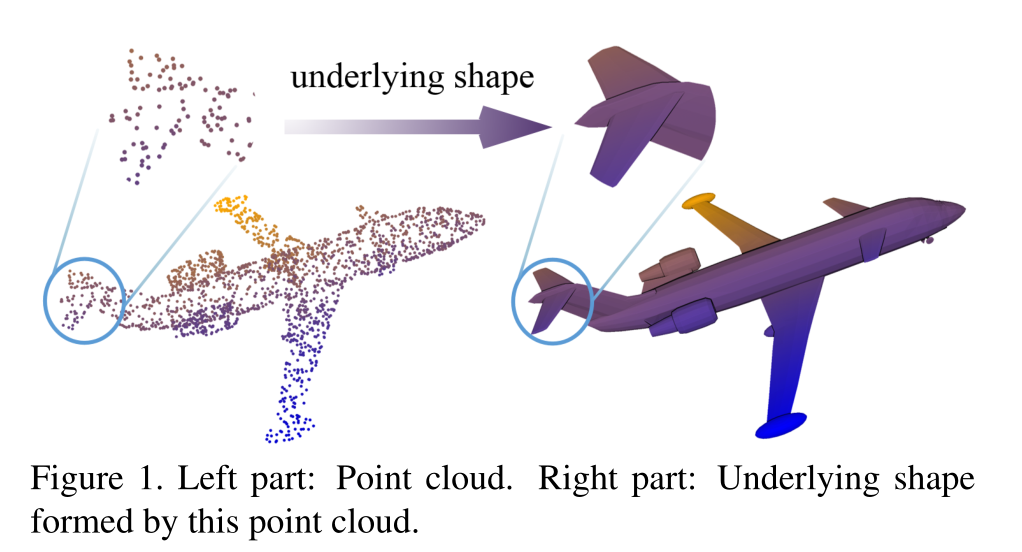
image

对于上图1我们很难推测这些不规则的点，如何组成一个基本形状。

在这里问题上，我们致力于将神经网络(CNN)在规则网格数据分析上的成功复制到不规则点云处理上。一些文章将点云转化为规则体素或多视图图像，然后使用CNN。然而这样的操作会导致3D点云的内在的几何信息丢失。之前的PointNet直接处理点云，独立的学习每个点并在最后聚合为一个final的全局feature representation，尽管影响深刻，但是他忽略了局部结构，并且局部结构已经在图像的CNN上被证明在抽象高级视觉上的重要性。为了解决这个问题，一些工作通过采样（PointNet++）或superpoint将点云划分为若干子集。然后建立层次结构，从局部到全局学习上下文表示。然而，这极为依赖于对局部子集的有效归纳学习，这是很难实现的。

通常情况下，学习点云集合\(P\in\mathbb{R}^3\)主要由三个挑战：(1)\(P\)是无序的，因此需要学习的东西是置换不变的；(2)\(P\)分布在三维几何空间中，因此要求学习的模型应该对其刚性变换（旋转和平移）有鲁棒性；(3)\(P\)形成一个潜在的形状，因此学习到的表征是应该可以判别形状的。

为此，我们提出了一种关系型神经网络(RS-CNN)，RS-CNN的关键是从关系中学习，例如点之间的几何拓扑约束，在我们看来，它可以在3D点云中编码有意义的形状信息。

具体地讲，每个局部卷积邻域都是以采样点\(x\)为中心，周围点为其邻域\(\mathcal{N}(x)\)来构造的。然后，卷积权重被迫从预定义的几何先验中学习高级关系表达式，即与\(x\)和\(\mathcal{N}(x)\)之间直观的低级关系。通过这种方式进行卷积可以获得关于点的空间布局的具有明确推理的归纳表示。他区别性的反映了不规则点形成的潜在形状，因此具有形状感知能力。此外还可以利用几何先验知识，包括对点置换的不变性和对刚性变换的鲁棒性。

  • 通过这种方式进行卷积可以获得关于点的空间布局的具有明确推理的归纳表示
  • 区别性的反映了不规则点形成的潜在形状，因此具有形状感知能力
  • 利用几何先验知识，包括对点置换的不变性和对刚性变换的鲁棒性
  • 利用类似CNN的层次结构，实现更大的感受野，以实现上下文形状感知学习

主要贡献如下：

  1. 提出了一种新颖的从关系中学习的卷积操作，称为RSCNN。
  2. 提出了一种关系型形状卷积的深层层次结构，将规则网格CNN扩展到不规则的形状上，实现点云的上下文形状感知学习；
  3. 这个东西很吊。。。。。。
  • PointNet忽略了local structures，但是这种local structures对于CNN的成功至关重要。
  • PointNet++将PointNet分层应用于点云的子集，

Superpoint提出将点云划分为几何元素。图卷积网络应用于相邻点创建局部图。

  • 但是上面的方法没有明确的建模点的局部空间结构，因此获取到很少的形状信息。

\(\color{red}{没有进行先验的几何建模，所以无法获取到足够的局部信息，因此目前的文章都是在模型上动手，\\利用关于点云的先验知识设计针对性模型，以获取更多的局部信息。}\)

一些工作将点云映射到高维空间，以方便经典CNN的使用。SPLATNet将输入点映射到稀疏网格上，然后使用双边卷积进行处理。

形状感知表征学习

点云分析的核心是鲁棒性的区分表示底层的形状。

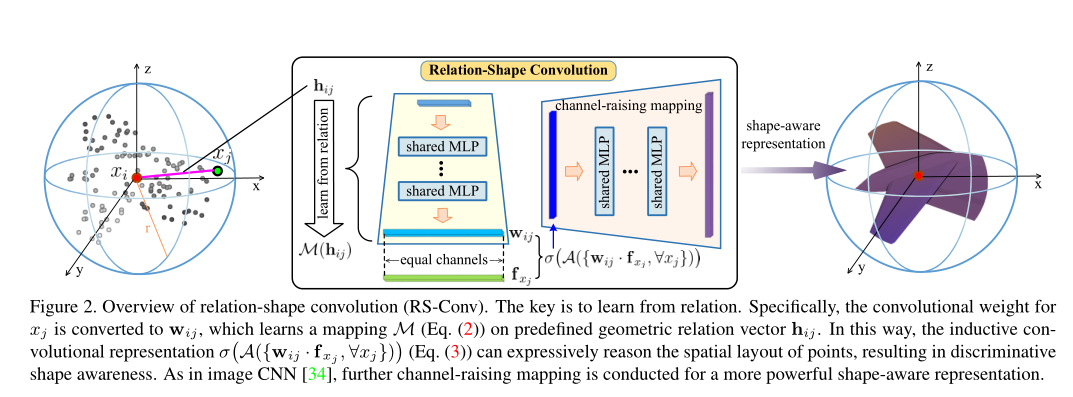
image

关系形状卷积

局部到全局学习在图像的CNN中取得了很叼的成功，这种方法很有搞头，但是它很依赖不规则点子集的形状感知归纳学习，这仍然是一个相当棘手的问题。

建模 为了解决这个问题，我们将局部点子集\(P_{sub}\in\mathbb{R}^3\)建模为球形邻域，采样点\(x_i\)作为中心点，周围点作为其邻域\(x_j\in\mathcal{N}(x_i)\)，上图2的最左边展示了这种建模方法。然后，我们的目标是学习这个邻域的归纳表示\(f_{P_{sub}}\)，它可以区分的编码潜在的形状信息。为了达到这个效果我们将一般卷积运算公式化为：

\[f_{P_{sub}}=\sigma(\mathcal{A(\{\tau(f_{x_{j}}),\forall x_j\})}),\ d_{ij}<r,\ \forall x_j\in\mathcal{N}(x_i)\tag{1} \]

其中\(x\)是一个\(3D\)点，\(f\)是一个特征向量。\(d_{ij}\)是在欧几里得空间上\(x_i\)和\(x_j\)的距离，\(r\)是球面半径。这里\(f_{sub}\)首先用函数\(\tau\)变换\(\mathcal{N}(x_i)\)中的所有特征，然后使用函数\(\mathcal{A}\)聚集他们，然后使用非线性激活器\(\sigma\)来获得以\(x_i\)为中心，\(r\)为半径的球体的特征。在上面的公式中\(\mathcal{A}\)和\(\tau\)是\(f_{P_{sub}}\)的关键。也就是说，只有当\(\mathcal{A}\)是对称的且\(\tau\)在\(\mathcal{N}(x_i)\)上的每个点是参数共享的，才能实现置换不变性。

经典CNN的局限性 在经典CNN中，\(\tau\)的实现方式是\(\tau(f_{x_j})=w_j\cdot f_{x_j}\)，其中\(w_j\)是可学习的权重，\(\cdot\)表示元素相乘。当应用于卷积的时候主要存在两个限制：（1）\(w_j\)不是共享的，导致点对点的差异和无法处理不规则的\(P_{sub}\)；（2）反向传播中\(w_j\)的梯度仅与孤立点相关，导致该种学习策略，无法为\(f_{P_{sub}}\)带来局部的形状感知和鲁棒性。

从关系中学习 我们认为从关系中学习可以缓解上述的限制。在三维空间的邻域当中，\(x_i\)与其所有邻域\(\mathcal{N}(x_i)\)之间的几何关系是关于点的空间布局的显示表达，它进一步区分的反映了原始的形状。为了捕捉这种关系，我们用\(w_{ij}\)替换经典CNN中的\(w_j\)，\(w_{ij}\)学习关系向量\(h_{ij}\)的映射\(\mathcal{M}\)，即\(x_i\)和\(x_j\)之间预定义的几何先验。我们称\(h_{ij}\)为低级关系，这个过程可以描述为：

\[\tau(f_{x_{j}})=w_{ij}\cdot f_{x_j}=\mathcal{M}(h_{ij})\cdot f_{x_j}\tag{2} \]

映射\(\mathcal{M}\)的目标是抽象出两点之间的高层关系表达式，从而对其空间布局进行编码。在这里我们使用共享多层感知机去实现\(\mathcal{M}\)。上图中间部分说明了该过程。通过这种方式\(w_j\)被巧妙地转化为\(w_{ij}\)，其梯度与\(x_i\)和\(x_j\)都相关。同时，\(\mathcal{M}\)在\(\mathcal{N}(x_i)\)中的所有电商完全共享，使得\(\mathcal{M}\)独立于点的不规则性。因此式1可以表示为：

\[f_{p_{sub}}=\sigma(\mathcal{A}(\{\mathcal{M}(h_{ij})\cdot f_{x_j},\forall x_j\}))\tag{3} \]

此种卷积可以将\(x_i\)和\(\mathcal{N}(x_i)\)之间的所有关系聚合在一起，可以实现关于点的空间布局的显示推理，从而产生有区别的形状感知。对于几何先验，可以使用3D欧几里得空间距离作为低级关系\(h_{ij}\)的直观描述。此外，\(h_{ij}\)还可以灵活定义，因为\(\mathcal{M}\)可以将其映射到高维关系向量，一边与\(f_{x_j}\)进行通道对其，以便于乘法计算。

通道提升映射 在公式3中\(f_{p_{sub}}\)的通道数和输入特征\(f_{x_j}\)的通道数是相同的。这个经典的CNN是不同的，后者是增加通道数，降低图像分辨率以获得更加抽象的表示。因此，我们在\(f_{p_{sub}}\)上添加了一个共享的MLP，用于进一步提升通道映射（如上图2中右所示）。

属性

等式3可以保持四个属性

置换不变性。 在内部映射函数\(\mathcal{M}(h)\)，底层关系\(h\)和共享mlp\(\mathcal{M}\)对点的输入都是置换不变的，因此，当外部汇聚函数\(\mathcal{A}\)是对称函数的时候，可以满足置换不变性。

对刚性变换的置换不变性。 这个性质在高级关系编码\(\mathcal{M}(h)\)中得到了很好的保持。当定义合适的\(h\)（3D欧几里得距离），他对刚性变换具有鲁棒性。

point interaction。 点不是孤立的，附近的点在几何空间中形成有意义的形状。因此，他们内在的相互作用对辨别形状至关重要，我们的relation learning明确的编码了点和点之间的关系，自然的捕捉了点之间的交互。

Weight Sharing。 这对于使用相同的学习函数在不同的不规则的点集上实现鲁棒性非常重要。

posted @ 2021-12-01 19:24  X-POWER  阅读(240)  评论(0)  编辑  收藏  举报