Generative PointNet: Deep Energy-Based Learning on Unordered Point Sets for 3D Generation, Reconstruction and Classification
Label:点网生成:在无序点云集合上的基于能量的深度学习去生成3D,重建和分类
摘要
我们以energy-based model的形式提出了一种针对无序点集合(如点云)的生成模型,这里的energy函数通过自底向上的输入置换不变网络去参数化。这个能量函数学习每个点的坐标编码然后把所有独立的点特征聚合到整个点云的一个energy里面。我们的模型可以用MCMC的最大似然估计来训练,而不需要类似GANs和VAEs那种辅助网络来实现。与大多数依赖于手工距离度量的点云生成器不同,因为他根据能量函数定义的统计特性,通过匹配观测示例去合成点云。此外,我们可以学习到一种基于能量模型的短周期MCMC,作为流状发生器用于点云重建和插值。学习到的点云表示可以用于点云分类。实验证明了所提出的生成点云模型的优越性。
介绍
背景和动机
和体素与mesh相比,点云可以提供一个简练且详细的对三维对象的表达。
点云生成模型是三维计算机视觉的基础问题,因为它提供了一个明确的概率分布,有利于点云的合成和分析任务。尽管对于点云的分类和分割任务在这几年取得了长足的进步例如PointNet,PointNet++,DeepSet, ShapeContextNet, PointGrid, Dynamic GCN, SampleNet,但三维点云生成模型的开发进展却相对滞后。其生成的主要挑战是与图像、视频和体素化的的格式不同,点云不是规则结构,而且无序的点集,这样使得将现有模型扩展到点云上很难。目前的3D生成模型的大部分工作都是基于体素数据的。
补全的难点:无序点集
现有补全方法:将点云数据体素化,然后推广现有的补全模型到体素上。
随着最近各种生成任务的成功,如图像和视频生成,研究人员对点云生成越来越感兴趣。他们大多基于完善的GAN,例如VAE等。或带有手工距离度量的encoder-decoder。本文提出了一种用于三维点云概率建模的生成模型。具体的讲就是模型是以EBM的形式直接定义在一个无序点集的概率密度函数。他的形式是基于能量的深度模型,他的能量函数的参数通过一个置换不变的自底向上的深度网络确定,该网络适用于定义无序点集上的能量。我们模型上的最大似然估计遵循的是Grenander所称的“综合分析”的方案。具体而言就是在每次学习迭代中,采用基于梯度的MCMC方法,通过Langevin dynamics sampling方法生成假3D点云数据。然后根据假样例和真观测样例之间的差异更新模型参数,根据函数定义的某些置换不变统计特性将假样例和真样例进行匹配。
- energy-based model
- 高度概括该文章下生成模型的方法
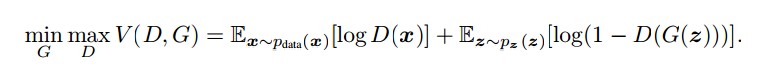
我们没有将分布的点隐式建模为一个自顶而下的生成器(隐式是因为生成器模型的边际概率密度需要对潜在噪声变量进行积分,这个是没法处理的。),也没有通过一个对抗性学习方法间接学习模型(在上面的公式中进行极大、极小的判别器、生成器训练。),或通过变分推理方案间接学习模型,将编码器用作推理模型来近似难以处理的后验分布。我们将此分布明确的建模为EBM并且通过MCMC-based MLE直接学习这个模型,而不需要额外的网络。极大似然估计不会遇到模型崩溃或者不稳定的问题,这个问题一般因为两种模型的不平衡训练程度而存在于GAN中。
-
提出一种规避
GAN模型崩溃的方法。 -
隐式建模的不可行原因
-
没有使用变分推理, 但是为什么没有使用呢? 上面好像上面好像没有回答。
-
拥有无限拟合能力的gan其能力的上限是很高的,但是由于两个模型的对抗和博弈,使得他们很难训练和收敛。有非常多的文论都在研究gan的收敛(纳什均衡)和稳定(mode collapse等)。
- 为什么不采用其他模型,优缺点对比。
使用编码器-解码器生成的点云模型,通常依赖手工制作的距离度量来度量两个点集之间的不相似性。我们模型的MLE学习对应于观测到的点云和生成的点云之间的统计匹配,其中统计属性由能量函数对学习参数的导数定义。因此,我们的模型并不依赖于手工制作的距离度量。
- 不依赖手工距离度量
- 手工距离度量? 看一下其他文章的点云生成方法。
如上所述,关于学习算法MLE学习算法采用“综合分析”方案,迭代如下两个步骤。
- 合成步骤:从当前模型生成假的合成的示例。
- 分析步骤:根据真实的观测实例和虚假的合成示例的差异,更新模型的参数。
下面是合成步骤的不同实现:
- 持久链,运行步数有限的
MCMC,例如郎之万动力,从之前的学习迭代中生成合成案例。 - 对比观察链,从观察到的案例中,运行有限步数的
MCMC。 - 非持久性短期MCMC,从高斯白噪声运行有限步MCMC。
- 按照方案1,可以学习到无偏模型,从而规避模型崩溃的可能性,但是学习非常耗时。
- 方案2会学习到一个有偏模型,但是通常无法生成真实的合成案例。
- 方案3,尽管学习到的模型仍然可能有偏差,类似于对比发散,但学习非常有效,并且由噪声初始化的短期
MCMC可以生成真是的合成示例。
此外,噪声初始化的短期郎之万动力学可被视为将初始噪声转换为合成案例的类流模型或类生成器模型。有趣的是,学习到的短期动力学可以重建观察案例和给不同的案例插值,类似于流模型和生成器模型。
在我们的工作中,我们采用了计划3。
我们证明了学习到的短期MCMC可以生成真实的点云模式,并且可以重建观测点云并在点云之间插值。此外,即使它学习了有偏模型,所学习的能量函数和特征仍然对分类有用。
相关工作
基于能量的建模和学习。基于能量的生成卷积神经网络目标在于学习EMB形式的数据的显示概率分布,其中能量函数由现代卷积神经网络参数化,MCMC采样基于郎之万动力学。在图像,视频,体素上显示了基于能量的生成的卷积神经网络学习复杂数据分布的令人信服的结果。为了使模型训练更加有效,研究科一些可供选择的抽样策略。例如,提出了基于能量的生成卷积网络模型的多网格学习方法。合作学习通过MCMC训练生成卷积神经网络,其中使用生成器去分期采样。提出了一个非收敛、非混合、非持久的短期MCMC,并将这个短期MCMC作为一个已学习的生成器模型。最近研究表明生成网络可以用VAE进行训练。然而上述工作中的模型,仅仅适用于具有规则结构的数据,但三维点云是一种无序点集,在本文之前没有人对其进行研究基于能量建模学习的问题。
- 对于三维点云,我们采用EBM对其进行建模
- 概括一下,本文相对于其他文章的创新点。
深度学习方法已经成功应用于点云中进行分类和分割等判别任务。PointNet是一种开创性的鉴别深度网络,通过设计置换不变性的网络体系结构,直接处理点云进行分类。对于点云的生成模型我们可以使用VAEs和带有启发式损失函数的对抗性自编码器,测量两个点集之间的不相似性。
我们的模型是我们能够绕过训练GAN或VAEs的复杂性,或者绕过为测量两个点集之间的相似性而设计距离度量的麻烦。
- 点云生成模型:
VAEs和启发式损失函数的对抗性自编码器。
贡献
模型:我们提出了一种新的EBM,通过设计一个输入置换不变的自底向上的网络作为能量函数,显示表示无序点集的概率分布。这是一个为点云数据提供显示密度函数的生成模型。这将为三维深度学习领域以及无序点集建模研究提供新的思路。
学习:在提出的EBMs下,我们建议采用非传统的短期MCMC来学习我们的模型,并将MCMC视为基于流的生成器模型,以便它可以同时用于点云重建和生成。通常EBM无法重建数据。这是第一个可以实现点云重建和插值的EBM。
独一无二性:与现有的点云生成模型相比,该模型具有一下的特性:(1)不依赖于额外的辅助网络进行训练;(2)它可以从判别网中导出;(3)它将合成和重建统一在一个框架中;(4)他将点云的显示密度(EBM)和隐式密度(作为潜在变量模型的短期MCMC)统一在一个框架中。
性能:与最先进的点云生成模型(如基于GAN和基于VAE的方法)相比,我们基于能量的框架在合成、重建和分类任务中以更少的参数获得了具有竞争力的性能。
生成模型
基于能量的无序点集模型
假设我们观察到一组来自特定类别对象的三维形状\(\{X_i,i=1\dots ,N\}\),每个形状由一组\(3D\)点\({X = \{x_k,k=1,\dots,M\}}\),其中每个点\(x\)是其\(3D\)坐标的向量加上可选的额外信息,如\(RGB\)颜色等。在本文中,为了简单起见,我们讨论的点仅包括\(3D\)坐标信息。
我们通过以下基于能量的模型定义形状的显示概率分布,每个形状本身就是一个三维点云。
这里的\(f_\theta(X)\)是一个评分函数,他将输入\(X\)映射到一个评分,并由自底向上的神经网络将其参数化。\(p_0(X)\propto exp(-||X||^2/2s^2)\)在高斯白噪声分布(\(s\)是个超参数,这边取值为\(0.3\)),\(Z(\theta) = \int exp[f_\theta(X)]p_0(X)dX\)是用来归一化的常数,确保分布中所有概率之和为1。包含参数\(\theta\)的能量函数\(\varepsilon_\theta(X) = -f_\theta(X)+||X||^2/2s^2\)定义了\(X\)的能量,低能量的点云\(X\)被赋予高概率。
- \(\varepsilon_\theta(X) = -f_\theta(X)+||X||^2/2s^2\)是能量函数
- \(p_\theta(X)\)是个啥东西呢?
- 其中\(E(X)\)一般表示为似然函数,对数似然函数。所以有时候求最大似然函数也被称为求最小能量。
- 能量函数\(E(X)=\frac{||X||^2}{2S^2}-f_\theta(X)\),能量越低\(p_\theta(X)\)的概率越高。
- 在分类问题中,对于特征\(X=\{x_1,x_2,\dots,x_n\}\)和标签\(y\in Y\),我们可以将以能量函数\(E(X,y)\),这时候能量函数代表着\(X\)和\(y\)的匹配程度,能量越低匹配程度越好。所以可以得到\(y^*=argmin_{y\in Y}E(X,y)\)。需要注意的是,这个最小化是用来判断结果的,没办法作为损失函数去训练E,目前猜测本文的特点就是将其可训练化。
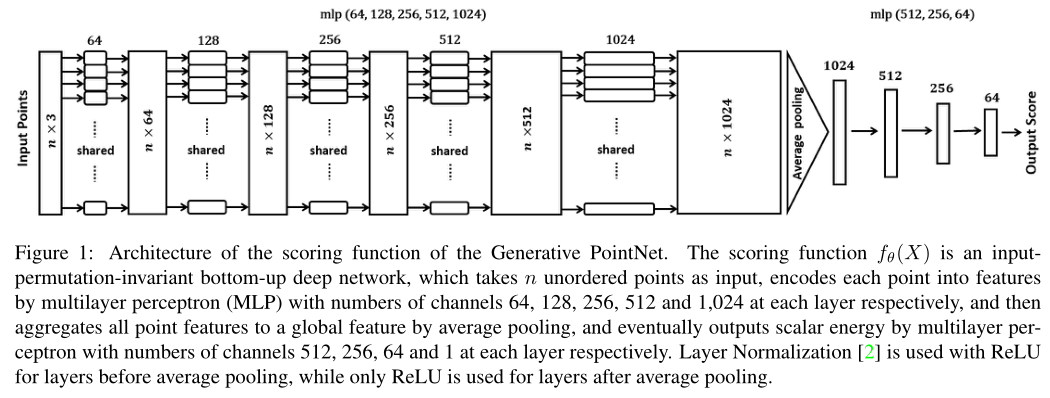
由于每个点云的输入\(X\)是一组无序点,对于能量函数\(||X||^2/2s^2\)已经是对顺序不敏感了。我们只需要将\(f_\theta(X)\)通过一个输入置换不变的自底向上的深度网络来对齐参数化,就可以得到一个能够处理无序点集的\(\varepsilon_\theta(X)\),这里对\(f_\theta(X)\)的处理类似于PointNet的处理方式。有关详细的处理见下图。
极大似然估计
假设我们观察到一组来自特定类别对象的三维点云\(\chi=\{X_i,i=1,\dots,N\}\)。\(q_{data}\)代表生成观察到的示例的分布,学习\(p_\theta\)的目的是从观察到的\(\chi\)中估计估计参数\(\theta\)。当\(N\)很大的时候,\(\theta\)的最大似然估计等价于最小化\(KL\)散度,\(KL(q_{data}||p_\theta)\),\(KL\)散度被定义为\(KL(q|p)=E_q[log(\frac{q(x)}{p(x)})]\),我们可以根据梯度上升的方法去更新\(\theta\),对数似然或者\(-KL\)散度可以通过下面的公式去计算:
- 这边梳理以下逻辑问题。
- 在生成模型里面,我们提出了\(p_\theta(X)\),这个东西应该是一个该点云\(X\)出现的概率或者说是分布的概率?
- 在这里我们指出学习\(p_\theta\)是为了估计参数\(\theta\)。
- 学习\(\theta\)的目的是 明确\(f_\theta\)???
- 阶段性总结, 这一段和之前的文章把整个网络模型拼凑的那个地步了?或者说数据走到那个节点了?
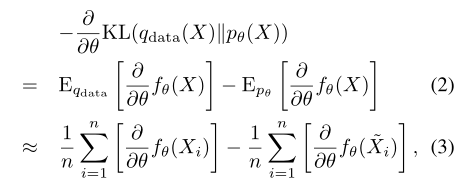
\(\{\widetilde{X}\,i=1,\dots,n\}\)是通过MCMC方法(如郎之万动力)根据当前\(p_\theta\)的分布生成的n个点云。式3,是为了解决式2的中难以处理的\(E_{p_{\theta}}[\dots]\),采用MCMC近似的方法去计算原本无法计算的梯度,采用mini-batch 综合分析的学习算法。在第t次迭代的时候,我们从训练数据集\(\{X_i,i=1,\dots,n\} \sim q_{data}\)中随机抽取一批观察样本,并从当前分布\(\{\widetilde{X}_i,i=1,\dots,n\}\sim q_{data}\)通过MCMC采样的方法,生成一个batch的合成样本。然后我们根据式3,去计算梯度\(\Delta(\theta_t)\)并且根据\(\theta_{t+1}=\theta_t+\gamma_t\Delta(\theta_t)\)和学习率\(\gamma_t\)去更新模型参数\(\theta\)。
基于郎之万动力的马尔科夫链蒙特卡洛采样
通过郎之万动力我们从\(p_\theta(X)\)的分布中去采样点云,我们迭代下面的步骤。
这里的\(\tau\)代表迭代步数,\(\delta\)是步长,\(U_\tau \sim N(0,1)\)是白噪声。由于\(f_\theta\)是可微函数,因此可以通过反向传播有效的计算\(\varepsilon_\theta(X_\tau)\)相对于\(X\)的梯度项。对于MCMC的初始化,以下三个是可选的方法:1、从噪声点云初始化长时间运行的非持久性MCMC;2、从噪声点云初始化持久MCMC,并在每个后续学习迭代中,从先前的学习迭代中生成的合成点云开始运行有限步的MCMC;3、在对比下面的差异,可以根据每个学习迭代中从训练数据集中采样的训练示例初始化MCMC;
短期MCMC生成模型
学习\(p_\theta\)需要MCMC采样去生成合成点云。学习到的\(p_\theta\)一般是多模态的,这是因为\(p_{data}\)一般也是多模态的,这是因为点云的复杂性和数据的大规模。多模态特性可能导致不同的MCMC链被局域模式捕获。因此,无论初始分布和马尔可夫链的长度如何,\(p_θ\)的MCMC采样可能需要很长时间才能混合。根据最近工作提出的解决方法,我们不再从\(p_\theta\)开始运行长期收敛的MCMC进行采样,而是从固定的初始分布(如高斯白噪声分布\(p_0\))开始,针对固定步数\(K\)下,只向\(p_\theta\)运行非收敛、非持续的短期MCMC。
我们用\(M_\theta\)去表示MCMC的K步向\(p_\theta(X)\)的转移核。对于给定的初始概率分布\(p_0\),从\(p_0\)开始运行MCMC的\(K\)步之后,样本\(X\)的结果边际表示为
由于\(q_\theta(X)\)不收敛,\(X\)高度依赖于\(Z\)。\(q_\theta(X)\)可被视为生成器模型、基于流的模型或潜变量模型,\(Z\)为以下形式的连续潜变量
其中,Z和X具有相同的维数,Z遵循已知的先验(高斯)分布p0。Mθ是短期朗之万动力学,包括式(4)中的K朗之万步,可将其视为K层剩余网络,噪声注入每层,并在每层上共享权重。设ξ为Mθ中由于分层注入噪声而产生的所有随机性。由公式(6)中所示的短期MCMC表示的模型可以通过“综合分析”方案进行训练,其中我们根据公式(3)更新θ,并根据公式(6)合成{X}。用短期MCMC训练θ不再是一个最大似然估计量,而是一个矩匹配估计量(MME),它解决了以下估计方程
尽管基于短期MCMC学习的\(p_\theta\)是\(p_{\hat{\theta}_{MEE}}\)而不是\(p_{\hat{\theta}_{MLE}}\),\(q_{\hat{\theta}_{MEE}}\)依然是一个有效的生成器,对三维点云的生成和重建依然是有用的。对于重建,给定一个测试样本\(X\),我们可以重建\(X\)通过找到\(Z\)去最小化重构误差\(L(Z)=||X-M_\theta(Z)||^2\),其中的\(M_\theta(Z)\)是无噪声版本的\(M_\theta(Z,\xi)\)(在学习之后,噪声项和梯度项相比可以忽略)。这可以很容易地通过在\(L(Z)\)上运行梯度下降来实现,\(Z\)从\(Z_0\sim p_0\)初始化。尽管我们在公式1中放弃了\(p_\theta\),在公式5中保留了\(q_\theta\),但\(p_\theta\)是至关重要的,因为\(q\)是由\(p\)衍生而来的,我们在\(p\)下学习了\(q\)。在其他研究中,\(p\)是\(q_{\hat{\theta}_{MEE}}\)的培养器。
当从大规模数据集中学习模型\(p_\theta\)的时候,只能负担有限的MCMC运算,学习一个短期MCMC作为\(p_θ\)点云生成和构建的生成器模型将是MCMC效率和MLE精度之间的权衡。
基于噪声初始化的短期MCMC学习方法类似于对比发散,它在每次学习迭代中从每个观测样本初始化一个有限步长的MCMC。对比发散也学习了一个偏差模型,但学习的模型通常不能合成,更不用说重建和插值了。对于噪声初始化的短期Langevin,可以优化诸如步长\(\delta\)等参数以最小化由短期MCMC引起的偏差。此外,我们模型的学习算法试图匹配\(\Phi_\theta(X)=\dfrac{\partial}{\partial \theta}f_\theta(X)\)。在关于深度神经网络理论理解的最新文献中,\(\langle \Phi_\theta(X),\Phi_\theta(X^\prime) \rangle\)的期望被称为神经切线核,前面公式的期望和\(\theta\)的初始化有关,他在理解深度和广度网络的优化和泛化中起着核心的作用。我们可以基于这样的内核定义度量,我们将在今后的工作中研究这些问题。
实验
其中代码部分在这里
合成
我们在ModelNet10上评估我们的3D点云合成模型,它也是一个在该方面的一个经典的基准测试样本。我们首先通过从ModelNet10数据集中每个对象的网格曲面均匀采样点来创建点云数据集,然后将其数据缩放到\([-1,1]\)范围内,我们为每一类点云训练一个模型。每个类别的训练数据在100到900之间,每个点云包含2048个点。
评分函数\(f_\theta(X)\)的网络架构可视化在Figure 1,具体操作看图可懂,不再扯了。
这里使用Adam作为优化器,初始学习率为\(lr=0.005\),betas=(0.9, 0.999),StepLR(optimizer, step_size=50, gamma=0.985),batch_size=128。并行的MCMC chain为128,我们运行K=64的郎之万 steps,step size \(\delta = 0.005\)。为了避免MCMC中的梯度爆炸发生,我们在每个Langevin步骤中讲梯度值剪裁到\([-1,1]\)的范围中,我们训练的时候用2000次迭代。为了改进效果每次在迭代的时候向观测样本中加入标准差为\(0.01\)的高斯噪声。
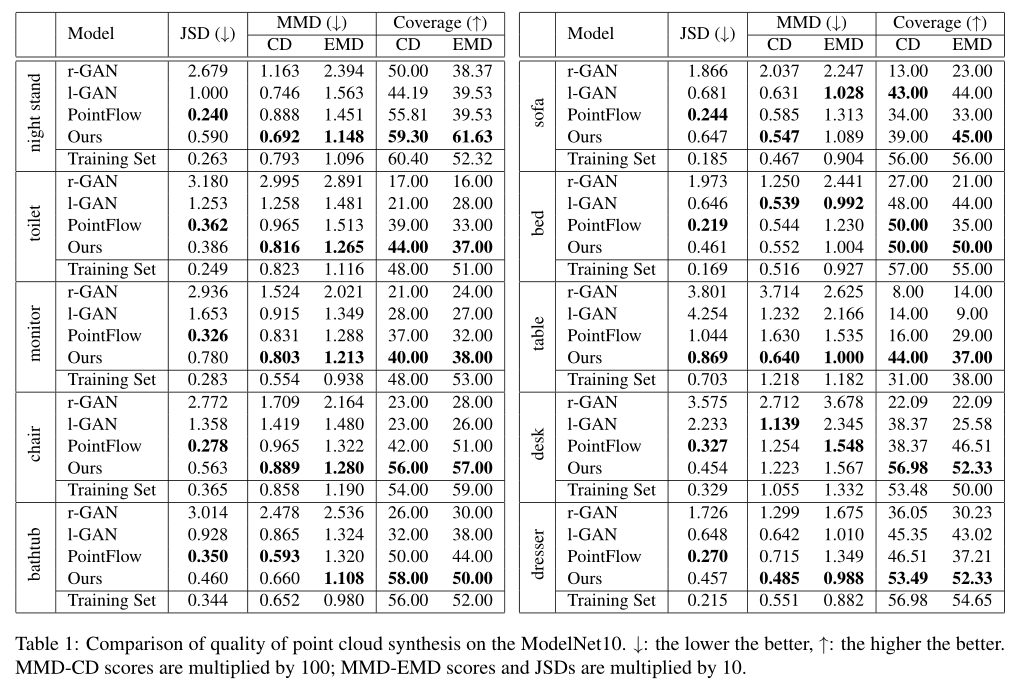
为了定量评估点云生成模型的性能,我们采用三种度量方式Jensen-Shannon Divergence,Coverage,Minimun Matching Distance,在评估Cov和MMD时,我们采用Chamfer distance(CD)和earth mover's distance(EMD)。我们将我们的模型和一些基准测试程序进行比较包括PointFlow,I-GAN和r-GAN。具体情况可以在Table 1处查看。我们使用他们官方代码展示了基准程序的表现,Figure 2展示了一些通过我们模型生成的一些点云的示例其中有椅子,桌子和浴缸。

重建
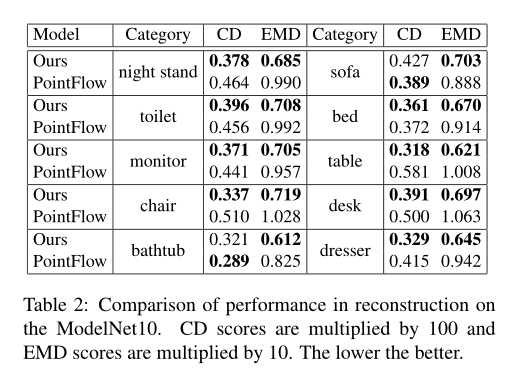
我们展示了GPointNet模型对3D点云的重建能力,我们使用一个短期的MCMC作为生成器去学习我们的模型。我们通过在前面讲的最小化重构误差去使用生成器重构它,正如我们在第三节 短期MCMC生成模型中讨论的那样 。Figure 3展示了重建未观察到的示例,第一行展示了需要重建的原始点云,第二行显示通过模型学习得到的相应的重建点云,第三行显示基准程序PointFlow获得的结果,该基准程序是基于Vae的框架。对于VAE来说,首先推断输入实例的潜在变量,然后通过生成器讲推断的潜在变量映射回点云空间,就可以很容易的实现重构。Table 2展示了我们的方法和PointFlow在点云重建方面的定量比较。这里我们采用CD和EMD的方法来度量重构质量,总的来讲,我们的方法优于基准程序。
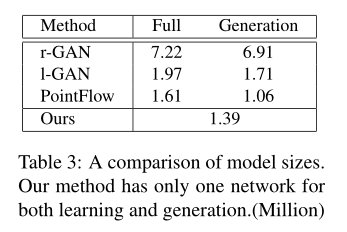
在模型的参数复杂度方面,我们在Table 3中比较了不同模型的参数的个数。基于GAN和Vae的模型使用了额外的辅助网络,其在训练和生成阶段的参数大小也有所哦不同 。但是我们的模型没有使用辅助网络所以我们的参数更少。
PointFlow的重建过程如下所示:
插值
下面看一下这个模型的插值能力。我们通过短期MCMC学习了该模型,我们首先从高斯分布中采样两个噪声点云\(Z_1\)和\(Z_2\)作为潜在空间的两个样本。然后我们在潜在空间使用线性插值的方法\(Z_p = (1-\rho)*Z_1+\rho*Z_2\),此处将\(\rho\)离散为\([0,1]\)内的八个值。我们通过\(X_p = M_\theta(Z_p)\)去生成点云。Figure 4通过显示生成的点云\(\{X_\rho\}\)序列显示了\(Z1\)和\(Z2\)之间的两种插值结果。平滑过渡和物理上合理的中间生成示例表明,生成器为点云嵌入学习一个平滑的潜在空间

面向分类的表征学习
评分函数\(f_\theta(X)\)中的点编码器\(h(X)\)可以用于点云的特征提取,用于有监督学习。我们通过ModelNet10数据集上执行分类实验来评估\(h\)。我们首先以无监督的方式在给出训练数据的所有示例上训练一个GPointNet。网络\(f_\theta(X)\)和前几节使用的相同,只是在这里我们在平均池化层之前添加了2048个通道,在平均池化层之后添加了一层1024个通道。我们在学习的评分函数中将平均池化层替代为最大池化层,并使用最大池化层的数据作为点云的特征。这样点云的特征提取器也是输入置换不变的,我们根据提取的特征从标记数据中训练SVM分类器进行分类。我们在测试数据集上使用one-versus-all规则对SVM分类器的准确度进行评估。Table 4展示了其他基准程序在该数据集上的11个结果和我们的结果。
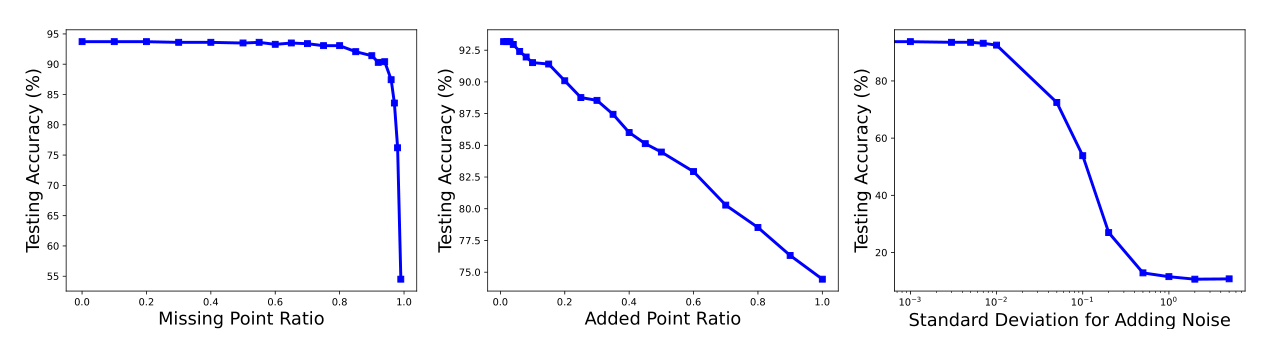
我们进行了实验去测试分类器的鲁棒性,我们考虑了以下三种情况的数据损坏:1、缺点,我们从每个点云中随机删除点。2、添加噪音,我们均匀添加分布在立方体中的额外点。3、扰动,我们通过对每个点云的每个点添加高斯噪声去扰动所有的点。在下面我们展示了这三种情况的分类精度。Figure 5展示了结果。
可视化点编码函数
评分函数学习每个点的坐标编码,然后将所有单独的点代码聚合为点集的分数。坐标编码功能由MLP实现,学习将每个三维点编码为我们用于分类的模型中的2048维向量。
结论
本文研究了基于深层能量的无序三维点云建模与学习。我们提出了三维点云的概率密度,即无序点集,其形式为基于能量的模型,其中能量函数由输入置换不变的深度神经网络参数化。该模型可以通过基于MCMC的最大似然学习进行训练,无需使用其他辅助网络。学习过程遵循“综合分析”方案。实验表明,该模型可用于三维生成、重建、插值和分类。为了更好地理解每个编码函数学习的内容,我们通过显示点云域中给出正滤波器响应的点,将MLP不同层上的每个滤波器可视化。在Figure 6中,我们在每一层随机显示4个过滤器。结果表明,不同层的不同过滤器可以学习检测不同形状区域中的点。较高层的过滤器通常检测形状比较低层复杂的区域中的点。