2023-2024-1 20231302《计算机基础与程序设计》第六周学习总结
作业信息
| 这个作业属于哪个课程 | 2023-2024-1-计算机基础与程序设计 |
|---|---|
| 这个作业要求在哪里 | 2023-2024-1计算机基础与程序设计第六周作业 |
| 这个作业的目标 | Polya如何解决问题、简单类型与组合类型、复合数据结构、查找与排序算法、算法复杂度、递归、代码安全 |
| 作业正文 | https://www.cnblogs.com/9q2z2z/p/17809813.html |
教材学习内容总结
《计算机科学概论》
- 本章先由poyla算法开始,告诉我们如何用计算机解决问题,解决问题应该以哪些步骤去进行。用伪代码介绍了介绍了一些算法,其中包括有简单参数的算法,复杂变量,搜索算法和排序,递归算法。最后介绍了信息隐蔽的概念,这里又一次地体现了抽象这一重要概念的重要性。
《C语言程序设计》
- 本章介绍了算法的概念,并且介绍了它的描述方法,后文着重通过流程图介绍了不同的算法语句,包括了单、双、多分支条件语句,并在其中介绍了条件运算符和条件表达式。多路选择的switch语句和逻辑运算符和逻辑表达式。并且学习了程序测试的有关内容。
教材学习中的问题和解决过程
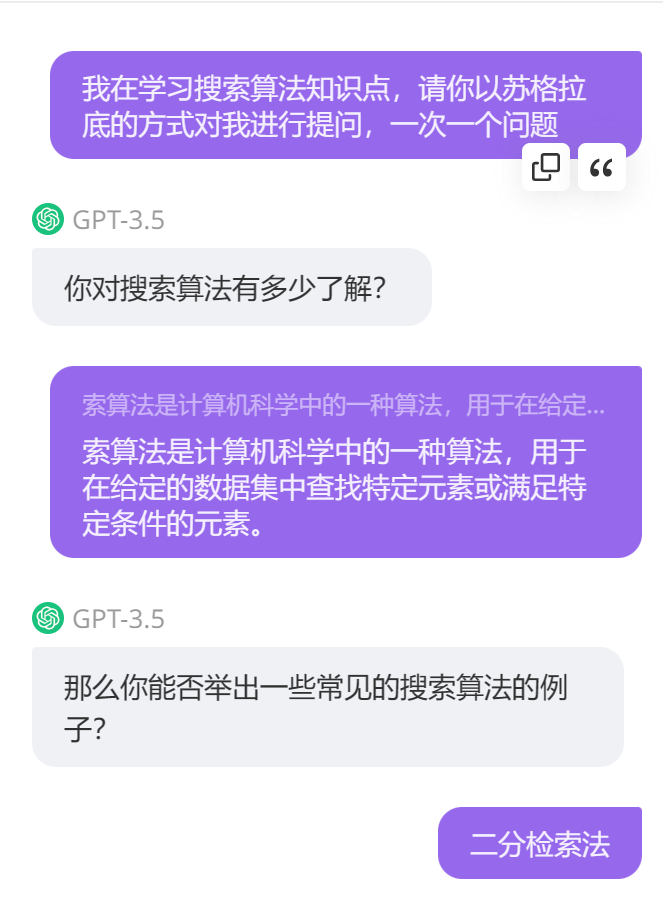
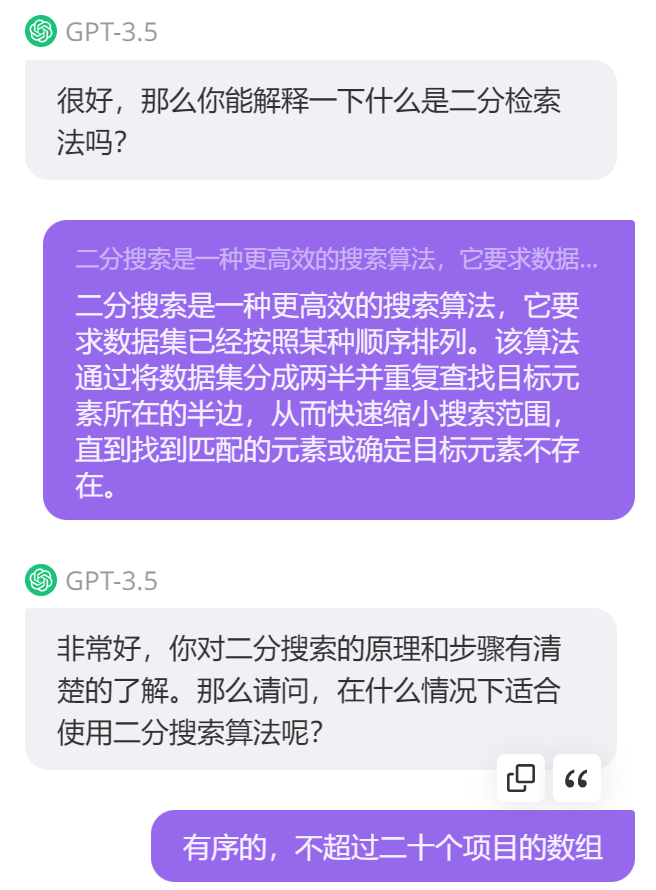
- 问题1:我在学习搜索算法时,学习到了顺序搜索、二分检索,它们都是基于有序排列的,但是一组数据如果没有顺序,是否就不能用搜索算法了呢,如果能的话,那个算法又是什么形式呢
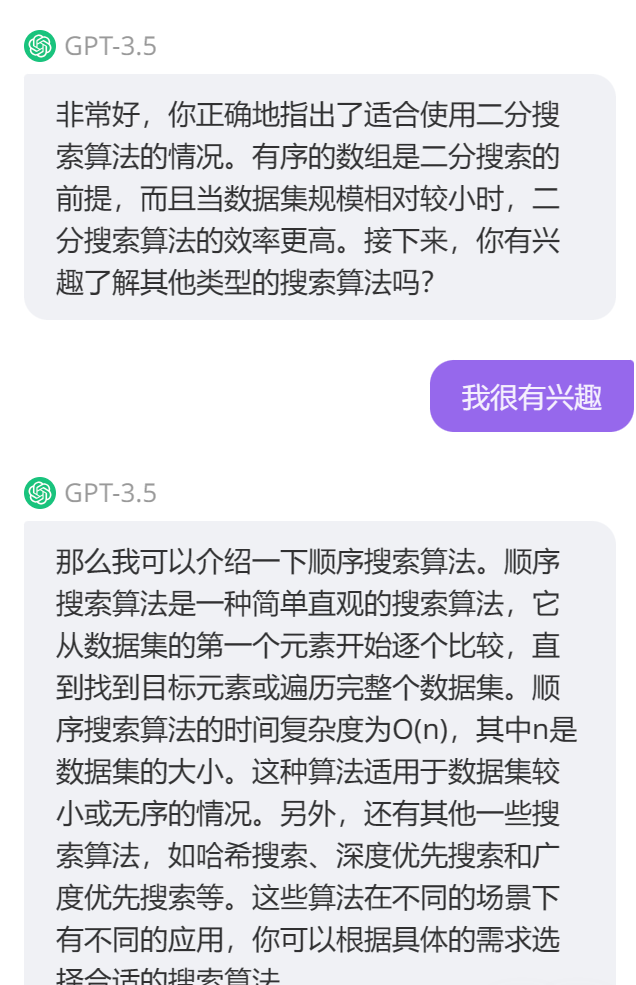
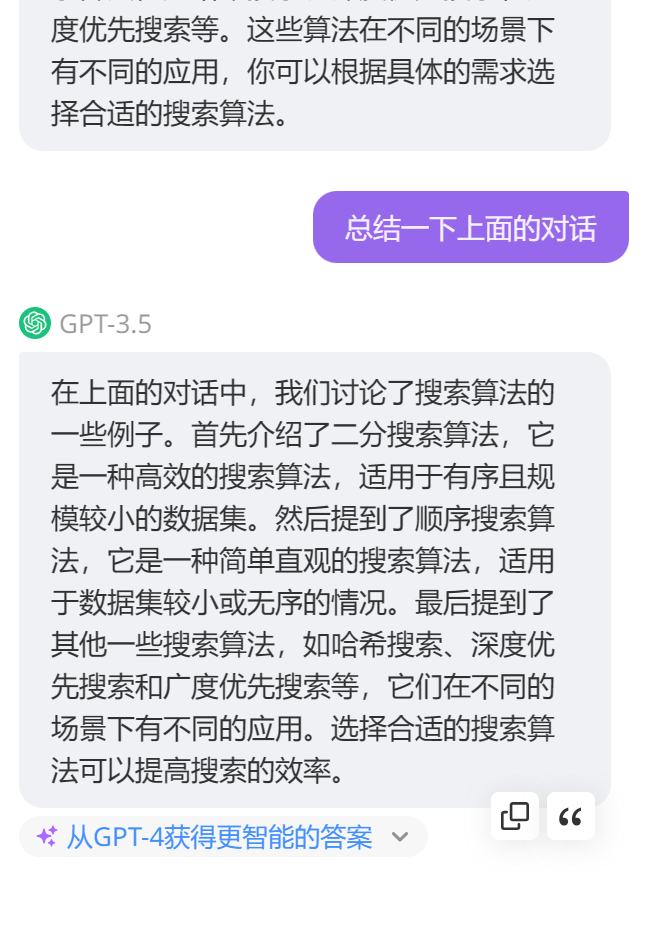
- AI回答:即使一组数据没有顺序,仍然可以使用搜索算法来查找特定元素。在无序数据中进行搜索的一种常见算法是线性搜索(Linear Search),也称为顺序搜索(Sequential Search)。
线性搜索算法从数据的开头开始逐个比较元素,直到找到目标元素或搜索完整个数据集。它的时间复杂度是O(n),其中n是数据的大小。
虽然线性搜索在无序数据中的效率较低,但对于小型数据集或者不需要频繁搜索的情况,它仍然是一种简单有效的搜索算法。
以下是一个示例的线性搜索算法的伪代码:
function linearSearch(array, target):
for i from 0 to length of array - 1:
if array[i] equals target:
return i
return -1
在这个伪代码中,我们遍历数组中的每个元素,如果找到目标元素,则返回其索引。如果遍历完整个数组仍未找到目标元素,则返回-1。
需要注意的是,线性搜索算法的效率取决于数据的大小,因此在大型数据集中,使用基于有序数据的搜索算法(如二分搜索)可能更加高效。但是对于无序数据,线性搜索仍然是一种可行的搜索算法。
- 问题2:书中提到递归法有程序运行效率低的缺点,并且讲到若提高程序运行效率,宜以迭代形式替代递归形式。我在这里想要了解一下迭代形式是什么样子的,通过一些例子了解一下它是怎样运行的。
- AI 回答
迭代形式是一种通过循环结构来实现算法逻辑的方法,相对于递归形式,它更加高效。在迭代中,算法通过迭代变量的更新和条件判断来控制循环的执行,直到达到预期的结果。
举个例子,我们可以通过迭代来实现计算一个数的阶乘。下面是使用迭代形式计算阶乘的示例代码:
int factorial(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
int main() {
int n = 5;
int result = factorial(n);
printf("The factorial of %d is %d\n", n, result);
return 0;
}
在这个例子中,我们使用了for循环来进行迭代计算阶乘。循环变量i从1逐步增加到n,每次循环将当前的i乘以result,并将结果存回result中。最终,当循环结束时,result中保存的就是n的阶乘值。
通过迭代,我们避免了递归中不断调用函数的开销,提高了程序的运行效率。迭代形式在C语言中是常见且重要的编程技术,可用于解决各种循环和迭代计算问题。
在第六行代码 result = i 中,= 是一个复合赋值运算符,用于将 result 乘以 i 的值,并将结果再次赋给 result。这行代码的作用是将当前的迭代变量 i 乘以 result 的值,然后将结果存回 result 中。
更详细地解释,result *= i 可以理解为 result = result * i。在每次循环中,result 的值都会与当前的迭代变量 i 相乘,并将乘积结果存回 result 中。这样随着循环的进行,result 逐渐累积乘积的值,最终得到 n 的阶乘。
例如,在计算阶乘 n 为 5 的情况下,初始时 result 的值为 1。在第一次循环中,i 的值为 1,所以执行 result *= i 后,result 的值变为 1。接着,在第二次循环中,i 的值为 2,所以执行 result *= i 后,result 的值变为 2。依此类推,直到循环结束,result 的值将变为 n 的阶乘,即 120。
这行代码的目的是不断更新 result 的值,使其保存当前迭代的乘积结果,从而最终得到整个阶乘的结果。
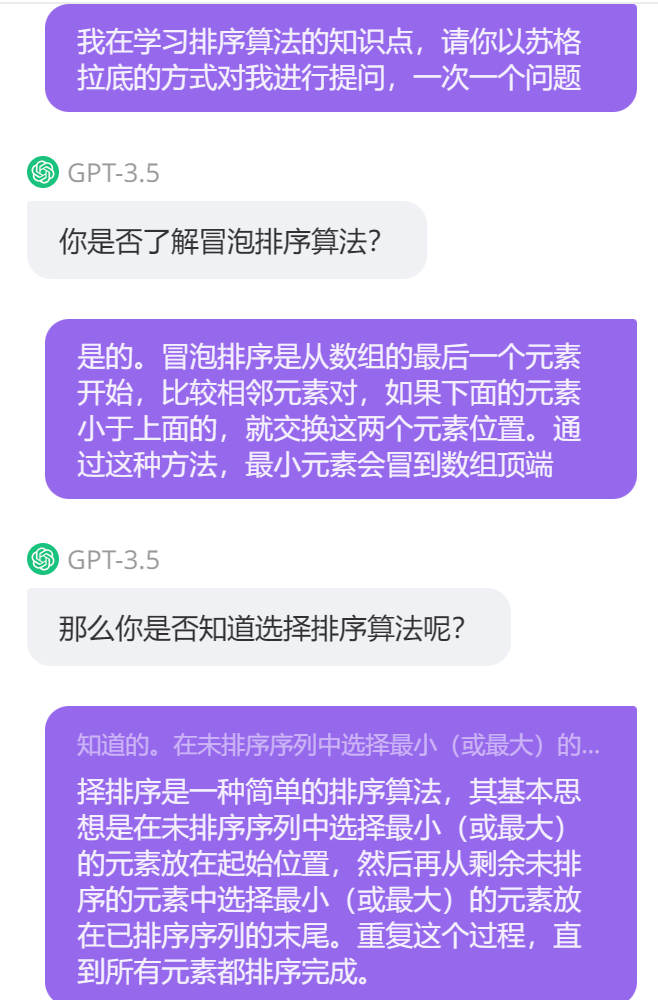
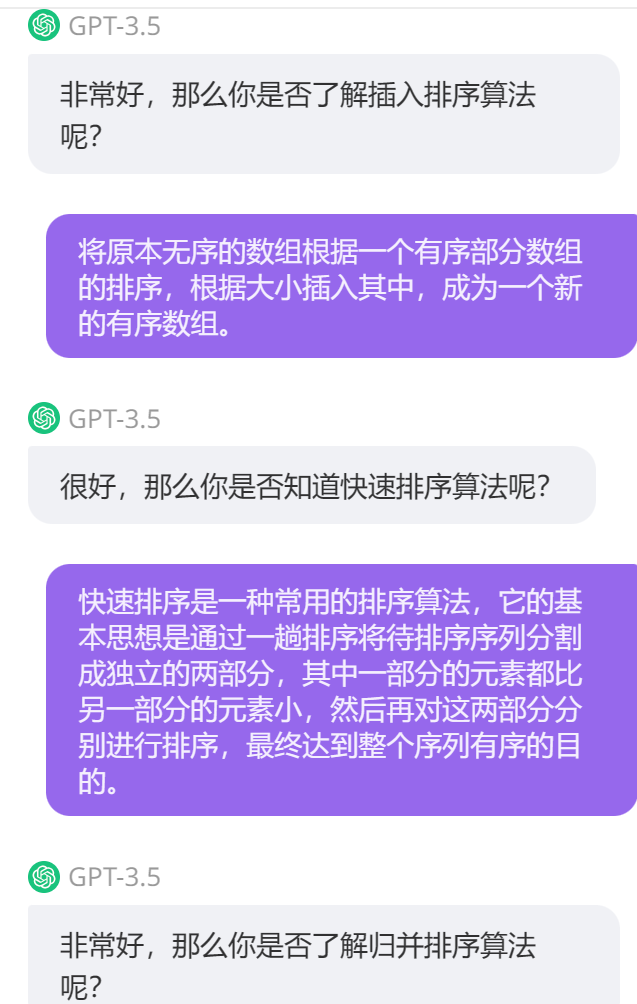
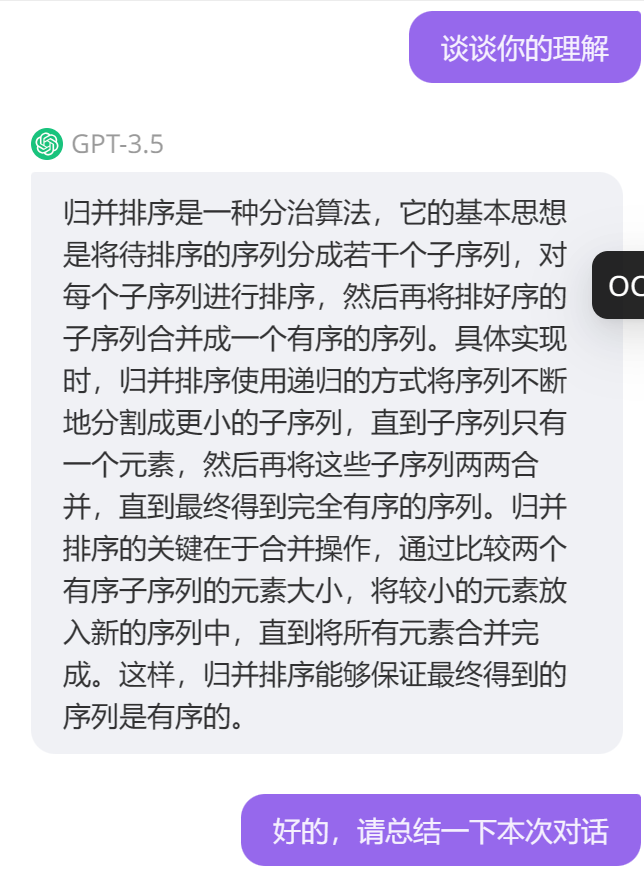
基于AI的学习