PCA原理及其代码实现

首先简述一下PCA的作用：

　　PCA是一种线性降维方法，它的目标i是通过某种线性投影，将高维的数据映射到低维空间中，并期望在所投影的维度上数据的信息量最大（方差最大），以此使用较少的数据维度，同时保留较多的原数据点的特性。

　　PCA降维的目的，就是为了尽量保证“信息量”不丢失的情况下，对原始特征进行降维，也就是尽可能将原始特征往具有最大投影信息量的维度上进行投影，将原始特征投影到这些维度上，使降维后信息量最小。

PCA算法主要步骤：

　　去除平均值

　　计算协方差矩阵

　　计算协方差矩阵的特征值和特征向量

　　将特征值进行排序

　　保留前N个最大的特征值对应的特征向量

　　将原始特征转换到上面得到的N个特征向量构建的新空间中

　　注：最后两步也就是实现了特征压缩

举个例子：

 

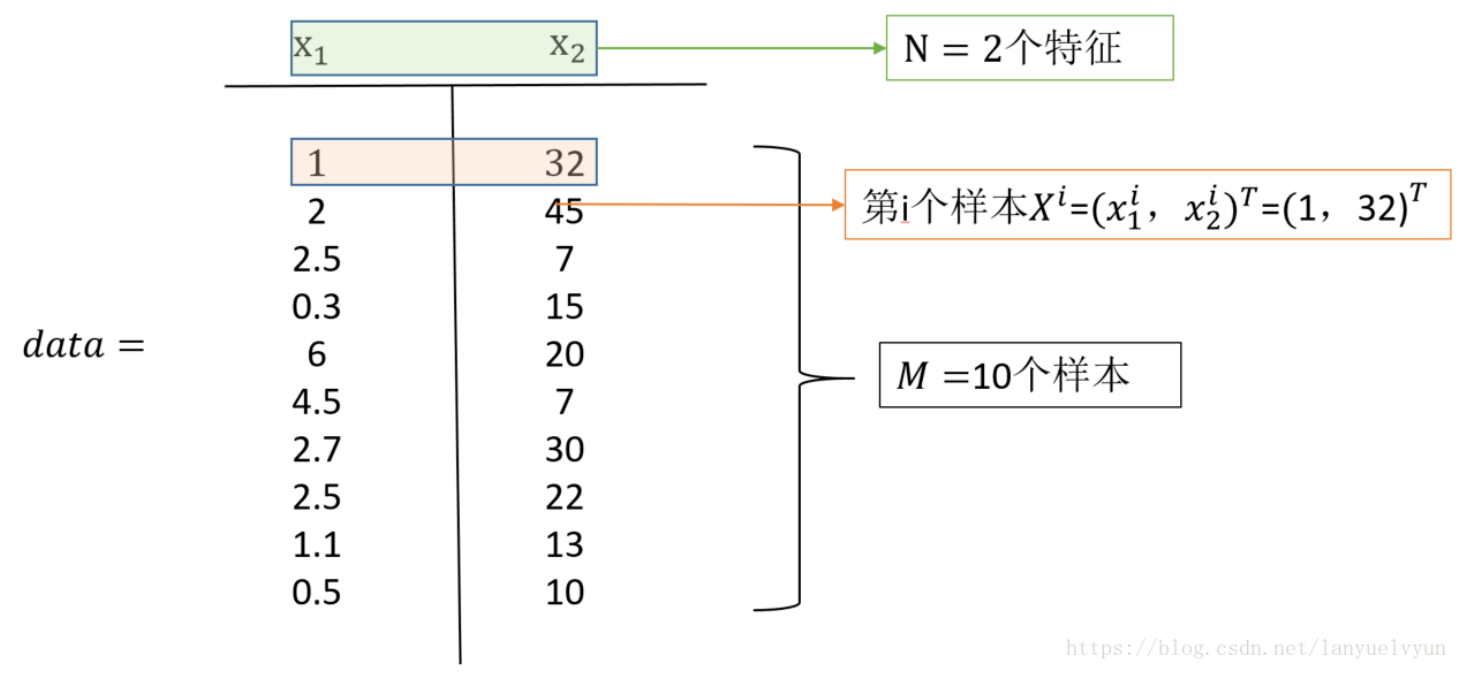
简单论述一下PCA相关的数学概念：

随机变量的数字特征：

　　均值：描述一维随机变量，表明信息是有限的

　　方差，标准差：描述一维随机变量的数据的“散布度”

　　协方差：度量两个随机变量关系的统计量

方差定义：

           

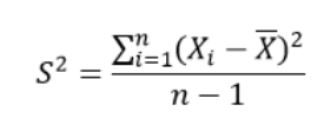
标准差定义：

　　

 

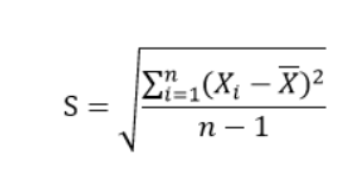
 协方差定义：

　　度量两个随机变量的相似程度，

　　

 

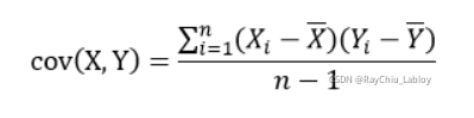
 详细步骤说明：

　　求每一个特征的平均值，然后对于所有样本，每一个特征都减去自身的均值，经过去均值的处理之后，原始特征的值就变成了新的值，在这个新的数据的基础上，在进行接下来的操作

　　求协方差矩阵C

　　

 

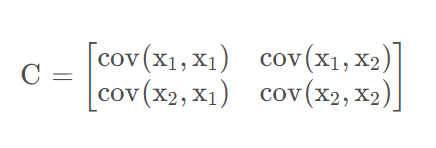
 　　上述矩阵中，对角线上分别是特征x1和x2的方差，非对角线上的是协方差。协方差大于0，表示x1和x2正相关，小于0表示负相关，等于0，互相独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

　　之所以除n-1，是因为这样能使我们以较小的样本集更好的逼近总体的标准差，即统计上的“无偏估计”。

　　求协方差矩阵C的特征值和相对应的特征向量

　　同线性代数中求解特征向量步骤一样！！！！！

为什么样本在“协方差矩阵C的最大K个特征值所对应的特征向量”上的投影就是k维理想特征？

　　根据最大方差理论：方差越大，信息量就越大。协方差矩阵的每一个特征向量就是一个投影面，每一个特征向量所对应的特征值就是原始特征投影到这个投影面之后的方差。由于投影过去之后，要尽量保证信息不丢失，所以要选择具有较大方差的投影面对原始特征进行投影，也就是选择具有较大特征值的特征向量。然后，将原始特征投影在这些特征向量上，投影后的值就是新的特征值。每一个投影面生成一个新的特征，k个投影面就生成新k个新特征。

代码实现：

import numpy as np

class PCA():
    # 计算协方差矩阵
    def calc_cov(self, X):
        m = X.shape[0]
        # 数据标准化
        X = (X - np.mean(X, axis=0)) / np.var(X, axis=0)
        return 1 / m * np.matmul(X.T, X)

    def pca(self, X, n_components):
        # 计算协方差矩阵
        cov_matrix = self.calc_cov(X)
        # 计算协方差矩阵的特征值和对应特征向量
        eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
        # 对特征值排序
        idx = eigenvalues.argsort()[::-1]
        # 取最大的前n_component组
        eigenvectors = eigenvectors[:, idx]
        eigenvectors = eigenvectors[:, :n_components]
        # Y=PX转换
        return np.matmul(X, eigenvectors)

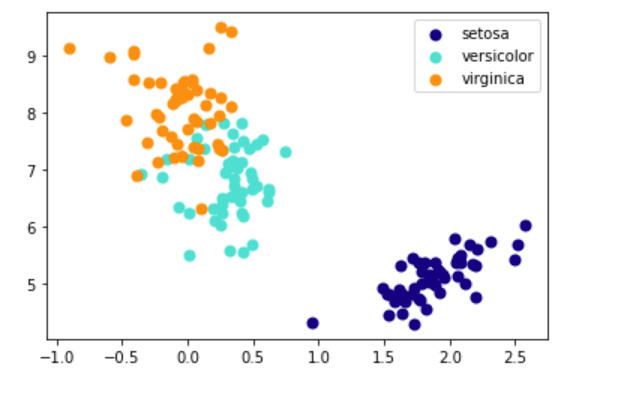
from sklearn import datasets
import matplotlib.pyplot as plt

# 导入sklearn数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 将数据降维到3个主成分
X_trans = PCA().pca(X, 3)
# 颜色列表
colors = ['navy', 'turquoise', 'darkorange']

# 绘制不同类别
for c, i, target_name in zip(colors, [0,1,2], iris.target_names):
    plt.scatter(X_trans[y == i, 0], X_trans[y == i, 1],
            color=c, lw=2, label=target_name)
# 添加图例
plt.legend()
plt.show()

结果：