GCN的原理及其代码实现

图数据的特征性质

　　图像数据是一种特殊的图数据，图像数据是标准的2D网格结构图数据。图像数据的CNN卷积神经网络算法不能直接用在图数据上，原因是图数据具有以下特殊性。

• 节点分布不均匀：图像数据及网格数据诶个节点只有4个邻接点，因此可以定义均匀的卷积操作，但是图数据节点的度数可以任意变化，即邻节点不确定，因此无法直接卷积。
• 排列不变性：排列不变性（置换不变性）表示输入的顺序改变不会导致函数结果的变化（例如函数f(x, y, z) = x × y × z）。图数据具有排列不变性，即在空间中改变图中节点（对图进行折叠扭曲）的位置对最后的图关系没有影响，而图像数据只有变更了两个像素的位置整个图像的表达会发生变化，因此无法使用卷积，因为卷积的方式不符合排列不变性。
• 节点的额外属性：图数据的每个节点具有自身的属性，即每个节点都具有自身的特征向量，相比如图像数据中的三通道表达更加丰富。
• 边的额外属性：图中的节点可以拥有权重和类型，在图像网格数据中边没有任何属性或者权重，CNN卷积神经网络也没有而已处理边的机制。

GCN与CNN

• GCN要解决的是不规则的图结构数据的通用的特征提取方案，考虑节点自身的属性以及节点的邻接节点属性获得节点的特征向量，最终实现图节点分类，回归等任务。
• GCN和CNN一样都是对节点/像素的周边节点/像素进行加权求和套激活函数作为特征提取，经过多轮特征提取之后最后被一层套类似softmax函数实现分类。

图知识储备

　　1）邻接矩阵

　　图的结构表示使用邻接矩阵（用A表示）进行表达，邻接矩阵就是统计Vij（V代表节点，ij代表从Vi->Vj）的连接权重，如果不考虑权重两个相连的节点的Vij值等于1，不相连的为0构成邻接矩阵，邻接矩阵是上下三角对称的。

 

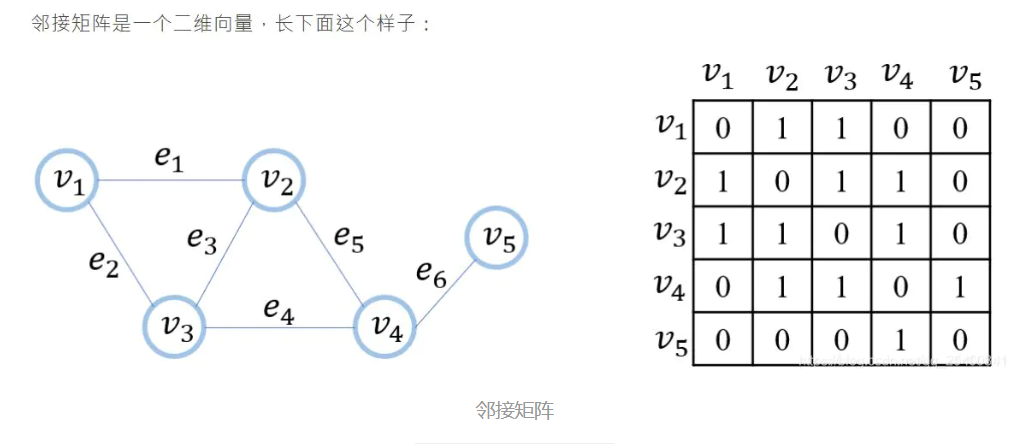
　　2）度矩阵

　　度矩阵（用D表示）是由节点的度构成的矩阵，度矩阵是对角阵，对角线上记录了各节点的度值，即Dii为节点i的度值，在无向图的情况下节点的度值是相连的边的数量，如上图度矩阵如下：

 

 

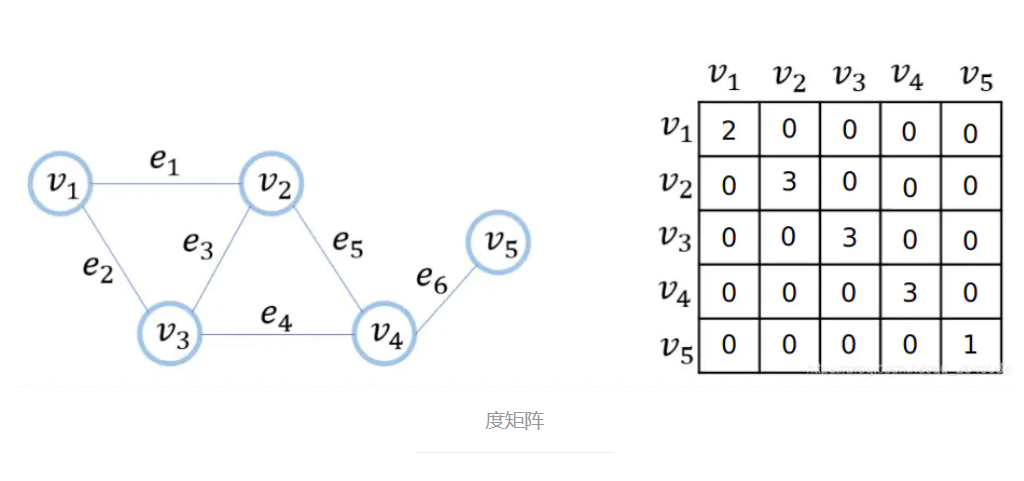
　　3）矩阵的逆

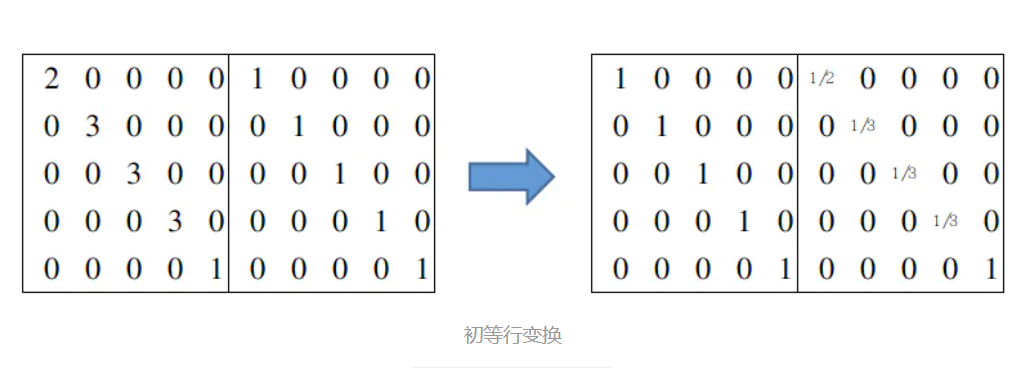
　　设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，E为单位阵，则称方阵A可逆，并称方阵B是A的逆矩阵。逆矩阵可以使用初等行变换求得，例如求上式的度矩阵，相当于每一行除以该节点的度。

卷积与图卷积的区别：

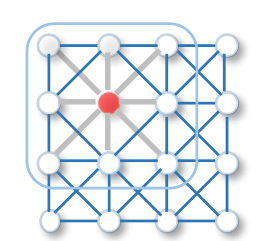
　　2d卷积：与图类似，图像中的每个像素都被视为一个节点，其邻居由过滤器的大小决定。二维卷积对红节点及其邻近节点的像素 值进行加权平均。

　　节点的邻居是有序的，并且具有固定的大小。如图列：

 

　　图卷积：图卷积。要获得红节点的隐藏表示，图卷积操作的一个简单解决方案是取红节点及其邻居的节点特征的平均值。

　　　　　　与图像数据不同的是，节点的邻居是无序的，大小是可变的。如图列：

 

 

GNN与网络嵌入的主要区别在于GNN是一组对各种任务设计的神经网络模型，而网络嵌入则涵盖了针对同一任务的各种方法。因此，GNN可以通过图自动编码器来解决网络嵌入问题。

另一方面：网络嵌入中包含了矩阵分解，随机游走等其他非深度学习方法。