算法导论阅读笔记(三)
优先级队列:
1、概述
队列是一种满足先进先出(FIFO)的数据结构,数据从队列头部取出,新的数据从队列尾部插入,数据之间是平等的,不存在优先级的。这个就类似于普通老百姓到火车站排队买票,先来的先买票,每个人之间是平等的,不存在优先的权利,整个过程是固定不变的。而优先级队列可以理解为在队列的基础上给每个数据赋一个权值,代表数据的优先级。与队列类似,优先级队列也是从头部取出数据,从尾部插入数据,但是这个过程根据数据的优先级而变化的,总是优先级高的先出来,所以不一定是先进先出的。这个过就类似于买火车票时候军人比普通人优先买,虽然军人来的晚,但是军人的优先级比普通人高,总是能够先买到票。通常优先级队列用在操作系统中的多任务调度,任务优先级越高,任务优先执行(类似于出队列),后来的任务如果优先级比以前的高,则需要调整该任务到合适的位置,以便于优先执行,整个过程总是使得队列中的任务的第一任务的优先级最高。
优先级队列有两种:最大优先级队列和最小优先级队列,这两种类别分别可以用最大堆和最小堆实现。书中介绍了基于最大堆实现的最大优先级队列。一个最大优先级队列支持的操作如下操作:
INSERT(S,x):把元素x插入到集合S
MAXIMUM(S):返回S中具有最大关键字的元素
EXTRACT_MAX(S):去掉并返回S中的具有最大关键字的元素
INCREASE_KEY(S,x,k):将元素x的关键字的值增加到k,这里k值不能小于x的原关键字的值。
2、最大优先级队列操作实现
采用最大堆实现最大优先级队列,关于最大堆可以参见上一篇日志http://www.cnblogs.com/Anker/archive/2013/01/23/2873422.html。
(1)HEAP_MAXIMUM用O(1)时间实现MAXIMUM(S)操作,即返回最大堆第一个元素的值即可(return A[1])。
(2)HEAP_EXTRACT_MAX实现EXTRACT_MAX操作,删除最大堆中第一个元素,然后调整堆。操作过程如下:将最堆中最后一个元素复制到第一个位置,删除最后一个节点(将堆的大小减少1),然后从第一个节点位置开始调整堆,使得称为新的最大堆。操作过程如下图所示:
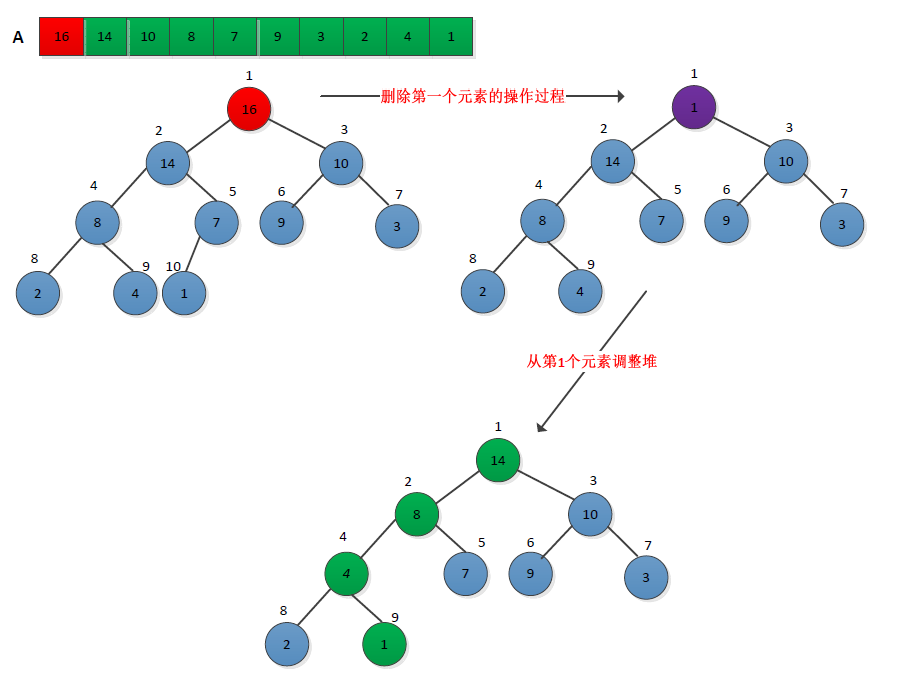
伪代码描述如下:
1 HEAD_EXTRACT_MAX(A) 2 if heap_size[A]<1 3 ther error 4 max = A[1] 5 A[1] = A[heap_size[A]]; 6 heap_size[A] = heap_size[A]-1 7 adjust_max_heap(A,1) 8 return MAX
(3)HEAP_INCREASE_KEY实现INCREASE_KEY,通过下标来标识要增加的元素的优先级key,增加元素后需要调整堆,从该节点的父节点开始自顶向上调整。操作过程如下图所示: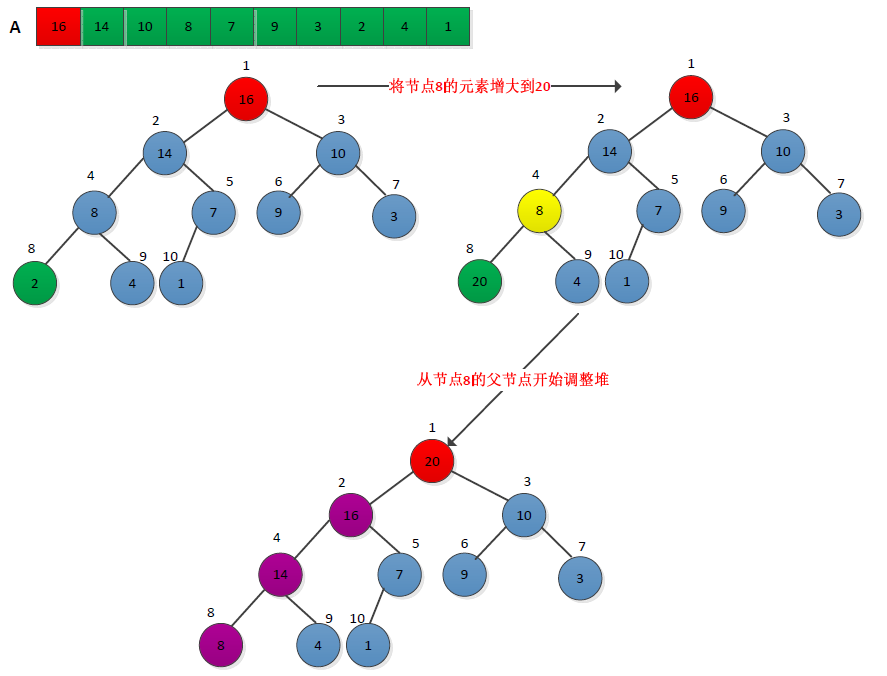
伪代码描述如下:
1 HEAP_INCREASE_KEY(A,i,key) 2 if key < A[i] 3 then error 4 A[i] = key 5 while i>1 && A[PARENT(i)] <A[i] 6 do exchange A[i] <-> A[PARENT(i)] 7 i = PARENT(i)
(4)MAX_HEAP_INSERT实现INSERT操作,向最大堆中插入新的关键字。新的关键字插入在优先级的队尾部,然后从尾部的父节点开始自顶向上调整堆伪代码描述如下:
1 MAX_HEAP_INSERT(A,key) 2 heap_size[A] = heap_size[A]+1 3 A[heap_size[A]] = -0; 4 HEAP_INCREASE_KEY(A,heap_size[A],key)
3、实例
问题描述如下:优先级队列中有多个事件发生,每个事件有自己独立的优先级,优先级是非负数,数值越大优先级越高。采用最大优先级队列模拟事件执行的优先顺序。具体操作包括:
(1)向优先级队列中添加一个新事件
(2)获取优先级队列中优先级最高的事件
(3)删除优先级队列中指定位置的事件
(4)增加优先级队列中指定位置事件的优先级
(5)降低优先级队列中指定位置事件的优先级
采用C++语言实现,完整程序如下所示:
1 #include <iostream>
2 #include <string>
3 #include <cstdlib>
4 using namespace std;
5
6 const static int QUEUELEN = 100;
7
8 class Event
9 {
10 public:
11 Event():eventname(""),priority(-1){};
12 Event(const string &en,const int p):eventname(en),priority(p){};
13 Event(const Event& en)
14 {
15 eventname = en.eventname;
16 priority = en.priority;
17 }
18 ~Event(){};
19 int get_event_priority()const
20 {
21 return priority;
22 }
23 string get_event_name()const
24 {
25 return eventname;
26 }
27 void increase_event_priority(const int k)
28 {
29 priority = priority + k;
30 }
31 void decrease_event_priority(const int k)
32 {
33 priority = priority - k;
34 }
35 void show_event() const
36 {
37 cout<<"Eventname is: ("<<eventname<<") and the priority is: "<<priority<<endl;
38 }
39 private:
40 string eventname;
41 int priority;
42 };
43 class PriorityQueue
44 {
45 public:
46 PriorityQueue();
47 void adjust_event(int index);
48 Event get_event()const;
49 void insert_event(const Event& en);
50 void increase_event_priority(int pos,int k);
51 Event delete_event(int pos);
52 void show_events() const;
53 ~PriorityQueue();
54 private:
55 Event *events;
56 int length;
57 };
58
59 PriorityQueue::PriorityQueue()
60 {
61 events = new Event[QUEUELEN];
62 length = 0;
63 }
64
65 PriorityQueue::~PriorityQueue()
66 {
67 if(!events)
68 delete [] events;
69 length = 0;
70 }
71 //adjust max heap
72 void PriorityQueue::adjust_event(int index)
73 {
74 int left,right,largest;
75 Event temp;
76 while(1)
77 {
78 left = index*2;
79 right = index*2+1;
80 if(left <= length &&
81 events[left].get_event_priority() > events[index].get_event_priority())
82 largest = left;
83 else
84 largest = index;
85 if(right <= length &&
86 events[right].get_event_priority() > events[largest].get_event_priority())
87 largest = right;
88 if(largest != index)
89 {
90 temp = events[index];
91 events[index] = events[largest];
92 events[largest] = temp;
93 index = largest;
94 }
95 else
96 break;
97 }
98 }
99 Event PriorityQueue::get_event()const
100 {
101 if(length != 0)
102 return events[1];
103 else
104 return Event();
105 }
106
107 void PriorityQueue::insert_event(const Event& en)
108 {
109 length = length + 1;
110 events[length] = en;
111 increase_event_priority(length,0);
112 }
113
114 void PriorityQueue::increase_event_priority(int pos,int k)
115 {
116 int i,parent;
117 Event temp;
118 if(pos > length)
119 {
120 cout<<"error: the pos index is larger than queue length"<<endl;
121 return;
122 }
123 events[pos].increase_event_priority(k);
124 i = pos;
125 parent = i/2;
126 while(i>1
127 && events[parent].get_event_priority() < events[i].get_event_priority())
128 {
129 temp = events[i];
130 events[i] = events[parent];
131 events[parent] = temp;
132 i = parent;
133 parent = i/2;
134 }
135 }
136
137 Event PriorityQueue::delete_event(int pos)
138 {
139 Event reten;
140 if(pos > length)
141 {
142 cout<<"Error:pos index is larger than queue length"<<endl;
143 return reten;
144 }
145 reten = events[pos];
146 events[pos] = events[length];
147 length--;
148 adjust_event(pos);
149 return reten;
150 }
151 void PriorityQueue::show_events() const
152 {
153 if(length == 0)
154 {
155 cout<<"There is no any event in the priority queue"<<endl;
156 }
157 else
158 {
159 cout<<"There are "<<length<<" events in the priority queue."<<endl;
160 for(int i=1;i<=length;i++)
161 {
162 events[i].show_event();
163 }
164 }
165
166 }
167 int main()
168 {
169 PriorityQueue pqueue;
170 Event en;
171 Event en1("fork",2);
172 Event en2("exec",3);
173 Event en3("wait",1);
174 Event en4("signal",6);
175 Event en5("pthread_create",5);
176 pqueue.insert_event(en1);
177 pqueue.insert_event(en2);
178 pqueue.insert_event(en3);
179 pqueue.insert_event(en4);
180 pqueue.insert_event(en5);
181 pqueue.show_events();
182 cout<<"\nThe max priority event is: "<<endl;
183 en = pqueue.get_event();
184 en.show_event();
185 cout<<"\nIncrese event3 by 7"<<endl;
186 pqueue.increase_event_priority(3,7);
187 en = pqueue.get_event();
188 en.show_event();
189 pqueue.show_events();
190 cout<<"\nDelete the first event:"<<endl;
191 pqueue.delete_event(1);
192 pqueue.show_events();
193 exit(0);
194 }
程序测试结果如下所示:

4、问题
(1)如何使用优先级队列实现一个先进先出的队列和先进后出的栈?
我的想法是:队列中的元素是先进先出(FIFO)的,因此可以借助最小优先级队列实现队列。具体思想是,给队列中的每个元素赋予一个权值,权值从第一个元素到最后一个依次递增(如果采用数组实现的话,可以用元素所在的下标作为优先级,优先级小的先出队列),元素出队列操作每次取优先级队列第一个元素,取完之后需要堆最小优先级队列进行调整,使得第一个元素的优先级最小。栈中的元素与队列刚好相反,元素是先进后出(FILO),因此可以采用最大优先级队列进行实现,与用最小优先级队列实现队列思想类似,按照元素出现的顺序进行标记元素的优先级,数据越是靠后,优先级越高。
举例说明采用最小优先级队列实现先进先出队列,现在有一组数A={24,15,27,5,43,87,34}共六个数,假设数组下标从1开始,以元素所在数组中的下标为优先级创建优先级队列,队列中元素出入时候调整最小优先级队列。操作过程如下图所示: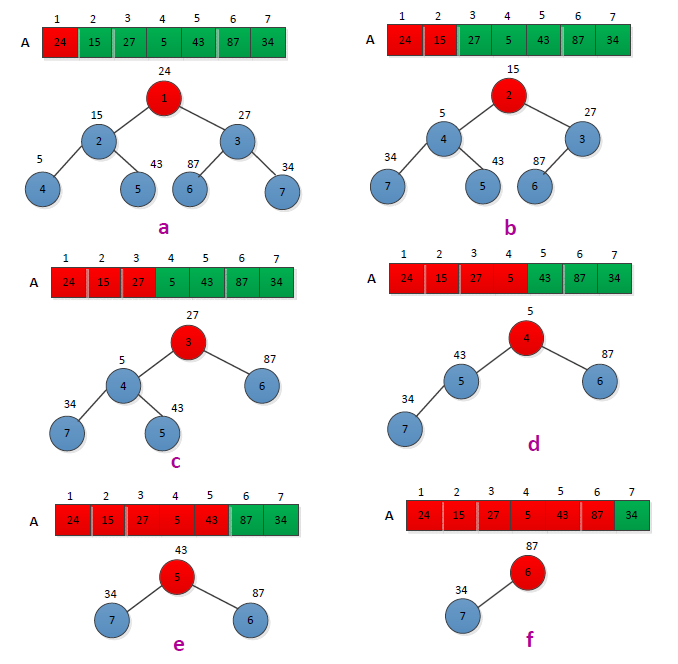



 浙公网安备 33010602011771号
浙公网安备 33010602011771号