DS博客作业05--查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 林进源 |
PTA得分截图
1.本周学习总结(0-5分)

1.1 查找的性能指标
- ASL成功:找到某一记录合集中任一记录平均所要的关键字比较的次数。
- ASL不成功:在某记录合集中找不到某一记录平均所要的关键字比较次数。
例:
- 比较次数:找到或者找不到某一记录的次数
- 移动次数:例如哈希表和哈希链有冲突时需要移位找到空的位置所需要的次数
- 时间复杂度:顺序查找:时间复杂度O(N),二分查找:时间复杂度O(logN)
1.2 静态查找
-
顺序查找
顺序查找:从表的一端开始,顺序扫描线性表,将扫描到的关键字与给定的K值相比较。当前扫描到的关键字与k相等,则查找成功,如果扫描结束后仍未找到关键字,等于K的记录则查找失败。
ASL成功=(n+1)/2
ASL不成功=n
平均时间复杂度:O(n)

-
二分查找
二分查找要求线性表示有序表,以折半的方式进行查找
二分查找,时间复杂度O(logN)
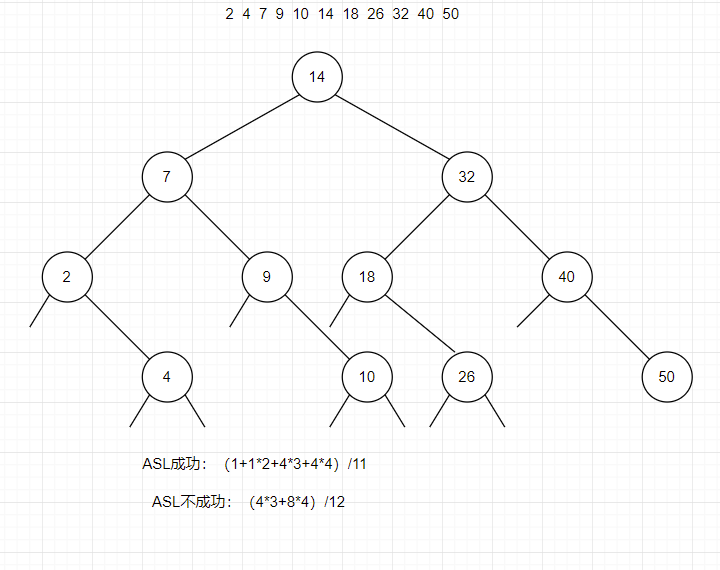
二分查找转换为二叉树的形式,进行判断查找
ASL成功=(对应层数 * 对应层的结点个数,进行累加)/总的结点个数
ASL不成功=(对应层数 * 对应层的空结点个数,进行累加)/总的空结点个数
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树(操作)
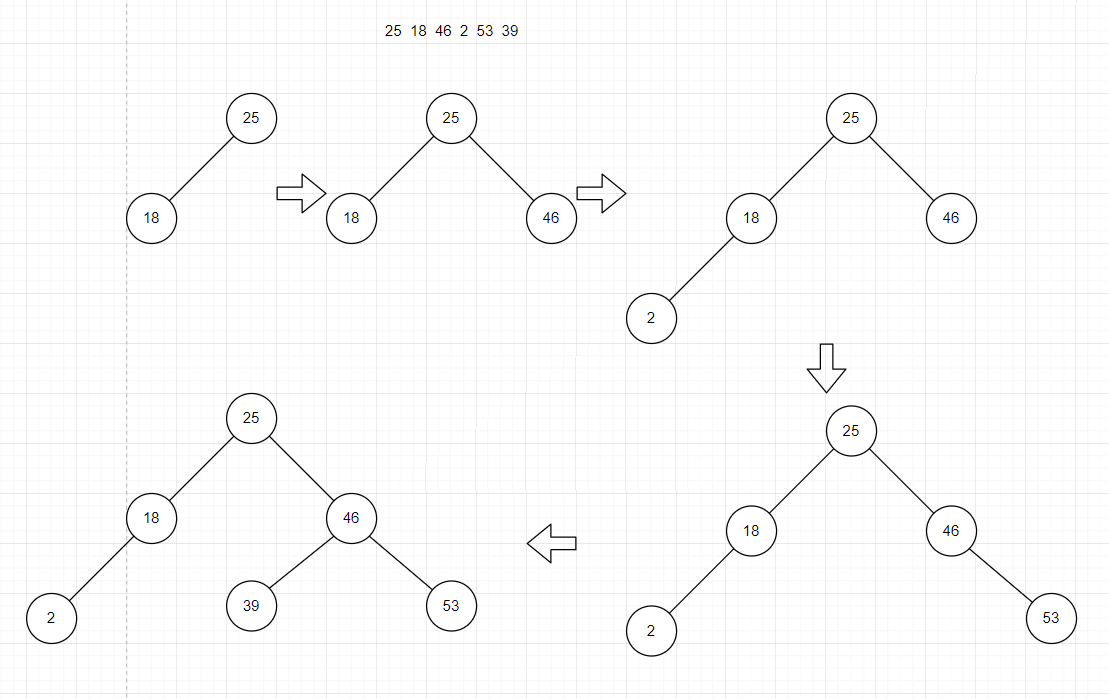
ASL成功=(1+2 * 2 + 3 * 3)/6
ASL不成功=(1 * 2 + 6 * 3)/7
ASL成功=(对应层数 * 对应层的结点个数,进行累加)/总的结点个数
ASL不成功=(对应层数 * 对应层的空结点个数,进行累加)/总的空结点个数
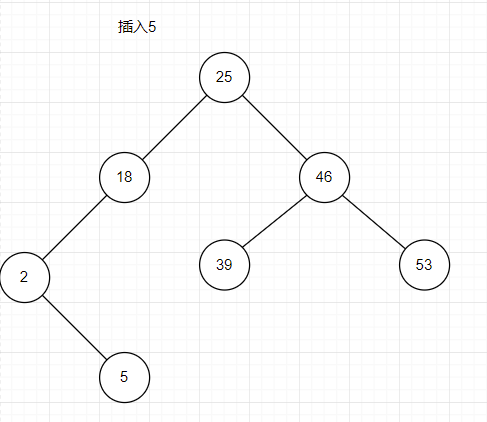
实现插入时,一般是在底层空结点的为止插入,通过比较找到符合条件的结点,插入要符合小在左,大在右的规律。
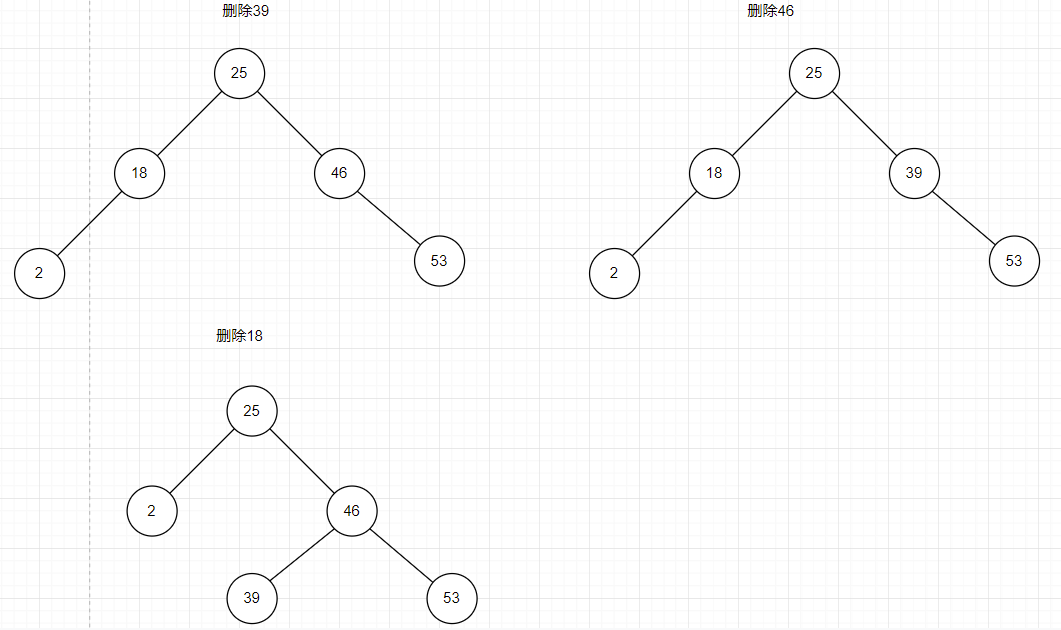
二叉树的删除分为三种情况:
第一种是删除叶子结点,直接将该节点为空即可
第二种是删除的结点只有左子树和右子树,删除该节点,将子树放在该节点对应位置
第三种是删除的结点有左子树和右子树,删除该节点,左子树的最大结点或者右子树的最小结点替代其对应位置,检查后序序列
上图对应三种情况
1.3.2 如何构建二叉搜索树(代码)
- 构建及构建:
void Insert(BinTree &T, int a)
{
if (T == NULL)//该结点为空则新建
{
T = new TNode;
T->data = a;
T->left = NULL;
T->right = NULL;
}
else
{
if (a > T->data)//进入右递归
{
return Insert(T->right, a);
}
else if (a < T->data)//进入左递归
{
return Insert(T->left, a);
}
}
}
进行边查边插入,为空时新建结点插入,小于结点值时进入左递归,大于结点值时进入右递归
时间复杂度为O(n)
删除:
BinTree Delete( BinTree BST, ElementType X )
{
BinTree p;
if (!BST )//树为空
{
printf("Not Found\n");
return BST;
}
if ( BST->Data > X)//进入左递归查找
{
BST->Left = Delete( BST->Left, X);
}
else if ( BST->Data < X)//进入右递归查找
{
BST->Right = Delete( BST->Right, X);
}
else
{
if ( BST->Right && BST->Left )
{
p = FindMax( BST->Left );//找左子树的最大结点
BST->Data = p->Data;//替代
BST->Left = Delete( BST->Left, BST->Data );//删除左子树的最大结点
}
else
{
p = BST;
if ( !BST->Left )//左子树为空
{
BST = BST->Right;
}
else if ( !BST->Right)//右子树为空
{
BST = BST->Left;
}
free(p);
}
}
return BST;
}
边查边删除,结点值小于要删除的值时进入右递归,大于要删除的值进入左递归,找到后判断是三种情况的哪一种,若没有孩子则直接删除,若只有一个孩子,则该孩子取代它。若有两个孩子,则将左子树的最大结点和右子树的最小结点替代它
时间复杂度为O(n)
利用递归算法可以减少不必要的比较次数,以一条最优解的路线进行查找,减少时间复杂度
1.4 AVL树
AVL树可适当减少树的高度,减少查找次数,优化其结构,减少时间复杂度,提高运行效率。
特点:所有节点左右子树深度差的绝对值小于等于1
平均查找长度:最坏情况O(long2n)
平衡调整:
- LL型调整
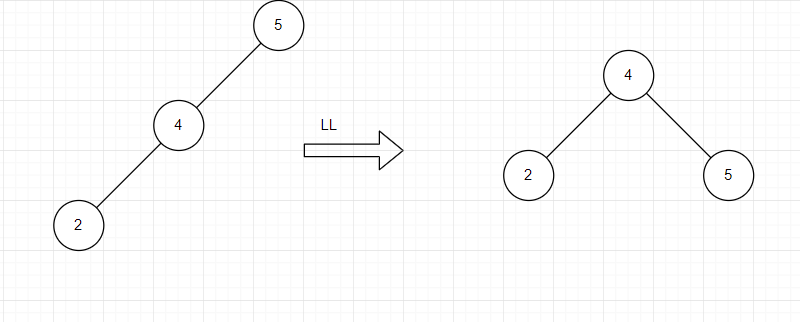
找到失衡结点进行分析,将失衡结点的左子树右上旋转作为根结点,原结点变为其右子树,并进行调整
- RR型调整
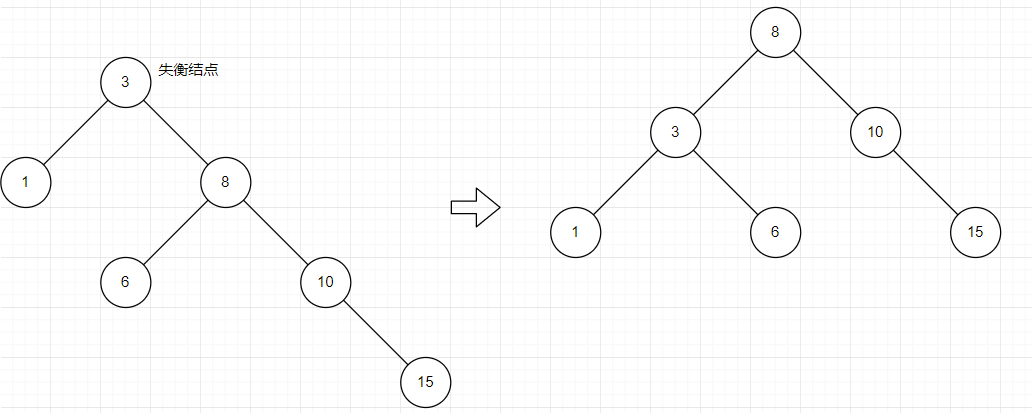
找到失衡结点进行分析,将失衡结点的右子树左上旋转作为根结点,原结点变为其左子树,失衡结点的右子树的左孩子变为失衡结点的右孩子,并进行调整。
- LR型调整
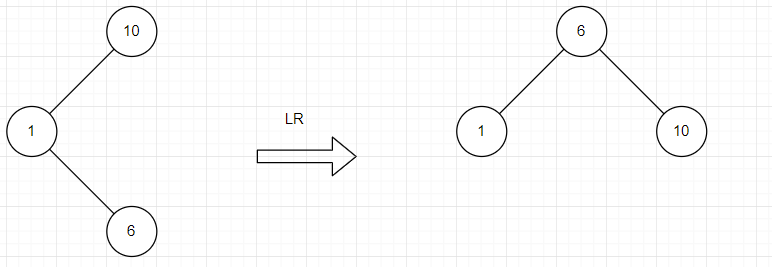
找到失衡结点进行分析,将失衡结点的左子树的右孩子上移变为根节点,失衡节点左子树变为其左孩子,失衡结点变为其右孩子,并进行调整。
- RL型调整
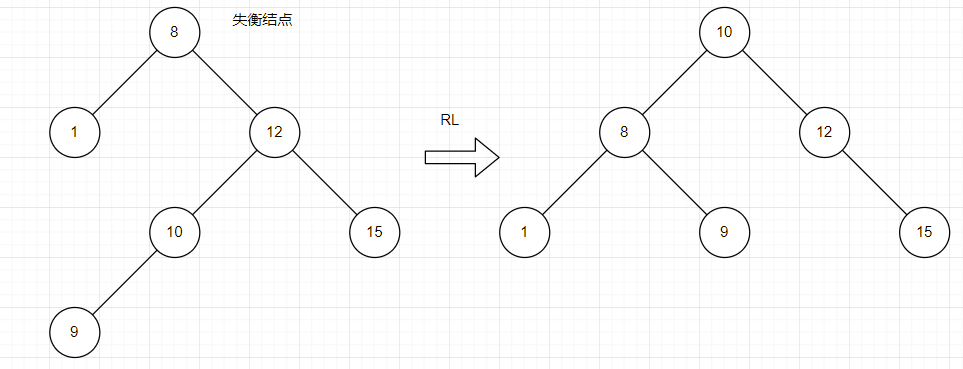
找到失衡结点进行分析,将失衡结点的右子树的左孩子上移变为根节点,失衡结点右子树变为其右孩子,失衡节点变为其左孩子,并进行调整
AVL树结点个数最少满足的条件:O(1)=1,O(2)=2,O(H)=O(H-1)+O(H-2)+1
n个结点的AVL树满足:h=log2(N(h)+1)
平均查找长度为O(log2n)
map用法
可利用map形成映射进行一对一的匹配,可与树的结构进行联立,第一个可以称为关键字(key),每个关键字只能在map中出现一次,第二个可能称为该关键字的值
模板:map<模板参数,模板参数>定义名称
#include <map> //STL头文件没有扩展名.h
插入函数:
方法一insert插入
例:
users.insert(pair<long long, string>(num, code));
users.insert(pair<long long, string>(10, 5))
方法二直接插入
例:
user[10]=code;
user[10]='5'
查找函数:
map<long long, string>users;
map<long long, string>::iterator iter;
iter = users.find(num);
if (iter == users.end())//到达结尾没找到
{
证明没找到;
}
其他基本函数(自己认为重要的):
clear() 删除所有元素
empty() 如果map为空则返回true
erase() 删除一个元素
find() 查找一个元素
insert() 插入元素
size() 返回map中元素的个数
1.5 B-树和B+树
- B-树
AVL由于一个结点只能存放一个关键字,若数据量太多会导致树的高度过高,B树的一个结点则可存放多个关键字,降低树的高度,减少查找时间。
一个m阶的B-树每个结点最多m个孩子结点,最多m-1个关键字。除了根节点外,其他结点至少m/2个孩子结点,至少m/2-1个关键字。根节点至少2个孩子。
B-树的查找是通过定义结点的孩子指针个数,通过比较该节点中的关键字,找到对应的孩子指针所指的元素,继续进行比较。
B-树的插入
插入过程要注意关键字的个数是否超过最大值,若超过了则要分裂,若有双亲结点,则中间值上移到双亲结点,若没有则新建一个双亲结点,树的高度加一。
例:
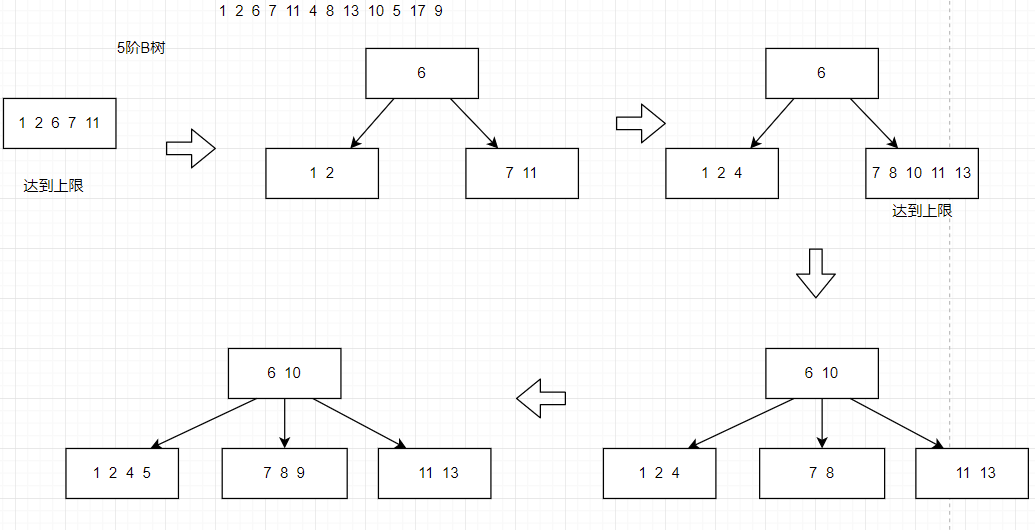
B-树的删除
删除时要注意关键字的个数是否少于最小值。若删除关键字后该节点的关键字个数仍然满足条件,则直接删除。若删除后不满足,则可观察其是否有孩子,若有孩子,且从其借一个关键字后仍满足条件,则可从其借一个孩子,若无法借到关键字,可合并孩子,重新进行分裂。
例:
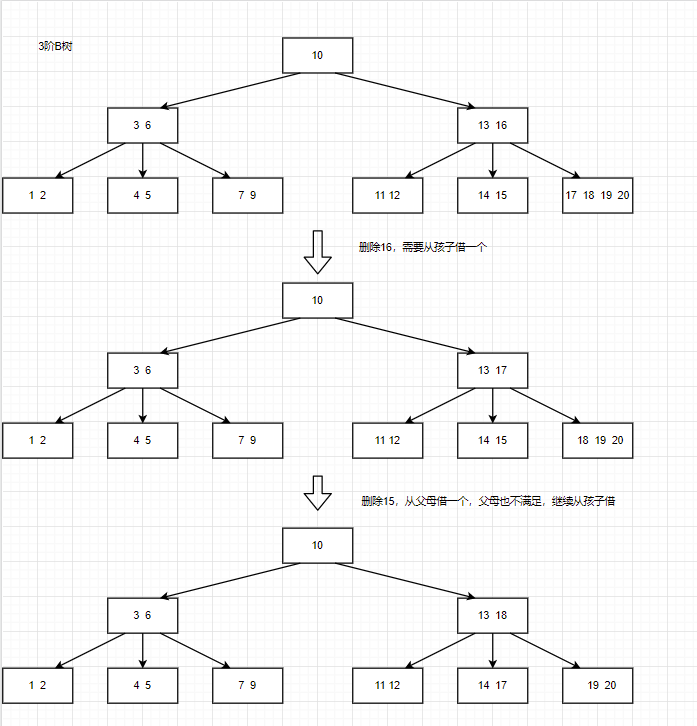
- B+树
与B-树的区别,若其结点有n棵子树则有n个关键字,所有的叶子结点中包含了全部关键字的信息,以及指向含这些关键字记录的指针,叶子结点本身依关键字的大小自小而则顶序链接。
可解决索引块系统一类的功能,例如文件查找索引
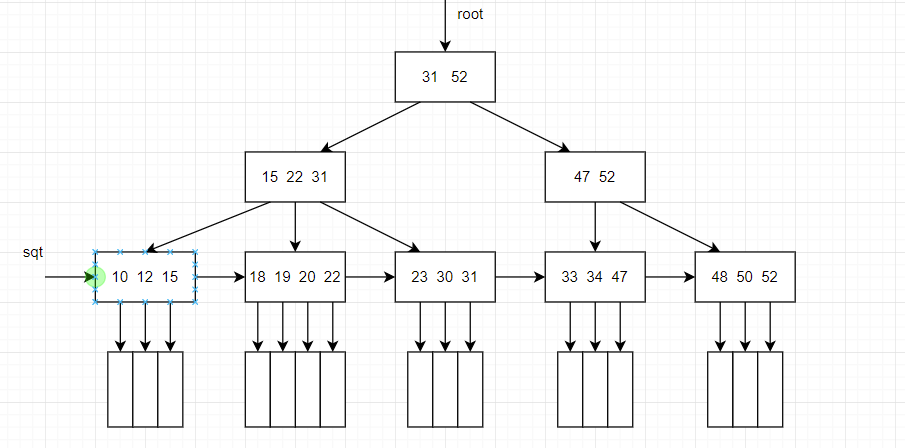
1.6 散列查找
哈希表(又称散列表),是一种存储结构,适用于记录的关键字与存储的地址存在某种关系的数据。设要存储的元素个数为n,再设计长度为m的连续内存单元,通过改变下标改变对应的映射关系,元素存储在内存单元中。
哈希表的设计:主要是为了解决哈希冲突。在实际应用中,哈希冲突是难以避免的,而它主要与三个因素有关。
哈希函数的构造方法可采用直接定址法和除留余数法,除留余数法中h(k)=k mod p,p取不大于m的素数时效果最好,减少发生冲突的可能。
- 哈希表
利用除留余数法确定对应的下标,当该位置已有元素时,自动往后一位移动,直至遇到空位,探测次数累次增加。
例题:
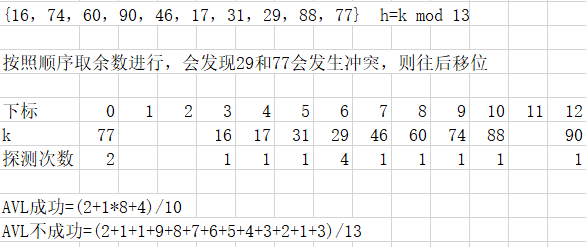
AVL成功=总的探测次数和/有效元素个数
AVL不成功=(从0开始到第p个单元格的不成功探测次数和,例如p为7,但建了大于7的单元格,只要计算0到6的单元格不成功探测次数即可)/p
- 哈希链
同样除留余数法确定对应的下标,但由于是建了链,当对应下标的链有元素时,采用头插法插入其中。
例题:
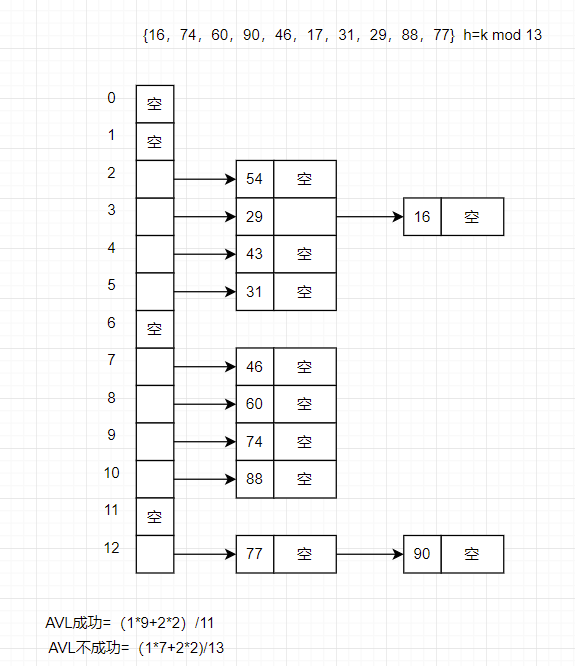
AVL成功=(按层来看,一列元素为一层,向外扩张。层数 * 对应层数的元素个数总和)/总元素个数
AVL不成功=元素总个数/p
2.PTA题目介绍(0--5分)
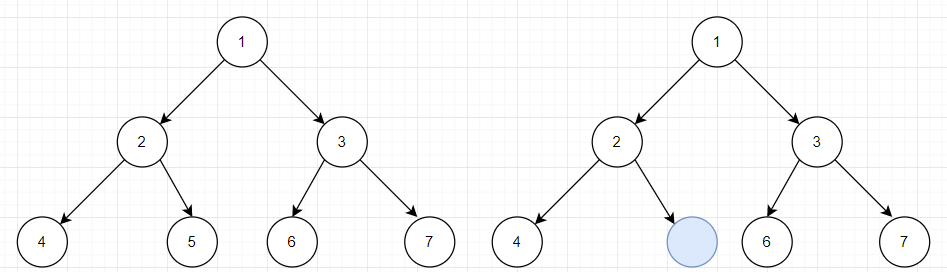
2.1 是否完全二叉搜索树(2分)
思路:通过上图可观察到完全二叉搜索树与不完全二叉树的区别,在于空结点出现的位置,不完全二叉树的空结点位置提前了,所以从该空结点的位置入手,通过层次遍历和计数法进行计数,遇到空结点停止,之后将此时的计数和元素总数进行比较,相等证明为完全二叉树。
2.1.1 伪代码
/*建立平衡二叉树*/
void Insert(BinTree &T, int a)
{
if (结点为空)
{
新建结并且初始化;
}
else
{
if (a < T值)进入右循环;
if (a > T值)进入做循环;
}
}
/*层次遍历*/
int falg = 0;
q.push(T);
while (!q.empty())
{
if (遇到空结点)
{
flag = 1;
}
else
{
if (flag = 0)进行计数;
左孩子入队;
右孩子入队;
}
}
2.1.2 提交列表

2.1.3 本题知识点
建立二叉排序树、层次遍历、flag计数法
2.2 航空公司VIP客户查询
航空公司VIP客户查询map写法
航空公司VIP客户查询哈希链写法
思路:一开始看到这个题目,想用map函数来写,也比较清楚,结果在测试时间上被卡了点,所以用哈希链的形式,先对哈希链构造结构体,之后对每个用户进行取余分组,找到对应的位置用头插法插入,并且判断对应的距离,但是测试点只能过第一个,后面两个测试点不知道是什么意思,代码也改了好久还是改不出来。
2.2.1 伪代码
/*结构体*/
typedef struct node
{
char id[20];
int distance;
struct Tnode *next;
}HashTnode,*HashList;
初始化哈希链;
输入数据;
/*取余求地址*/
int adr = 0;
for (int i = 12; i <= 16; i++)
{
换成数据;
}
/*查找用户是否已存在*/
node = h[adr]->next;
while (遍历哈希链)
{
比较用户名;
}
/*存放数据*/
if (用户存在)
{
比较路程;
存放数据;
}
else
{
新建结点;
比较路程存放数据;
}
2.2.2 提交列表
2.2.3本题知识点
构建哈希链结构体、取余求地址方法、头插法建链、map相关知识也可以适用本题
2.3基于词频的文件相似度
思路:这里采用了map的写法,定义map<string, bool>m[101]的形式,当第i个文件有word词组时,m[i][word]=true,这样就可以通过比较m[i]与m[其他]里面的其他词组,之后定义二维数组存放相似的词组个数,same[i][j]表示第i个文件与第j个文件中相同的词组个数。
2.3.1 伪代码
map<string, bool>m[101];//如果第i个文件存在单词word,则m[i][word] = true;
static int same[101][101];//定义二维数组存放是否有相似
static int num[101];
输入文件个数
for (到达文件个数)
{
while (直到遇到'#')
{
全部字母变为大写;
if (字母个数小于10)
逐个放入数组;
if (字母总个数大于3)
则map[i][word] = true;
}
for (it = m[i].begin(); it != m[i].end(); it++)
{
for (j = 0; j <= i; j++)
{
if (m[j][it->first] == true)//i中的词组在j中出现
same[i][j] = same[j][i] += 1;
}
}
记录第i个文件的词组总数放入num[i]中;
}
遍历计算相似度;
2.3.2提交列表

2.3.3本题知识点
map相关知识和运用、map与矩阵相联立解题