稀疏自动编码之神经网络

考虑一个监督学习问题，现在有一些带标签的训练样本(x(i),y(i)).神经网络就是定义一个复杂且非线性的假设hW,b(x)，其中W,b 是需要拟合的参数.

下面是一个最简单的神经网络结构，只含有一个神经元，后面就用下图的形式代表一个神经元：

把神经元看作是一个计算单元，左边的x1,x2,x3 (和 截距+1 )作为计算单元的输入，输出为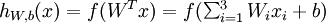：\textstyle h_{W,b}(x) = f(W^Tx) = f(\sum_{i=1}^3 W_{i}x_i +b)，其中，函数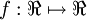f : \Re \mapsto \Re被称为激活函数，在这里我们的激活函数是sigmoid函数：

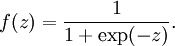
f(z) = \frac{1}{1+\exp(-z)}.

 

还有一种激活函数是正切函数（tanh function）:

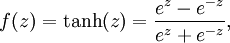
f(z) = \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}},

下面是两种激活函数图像：

                                               

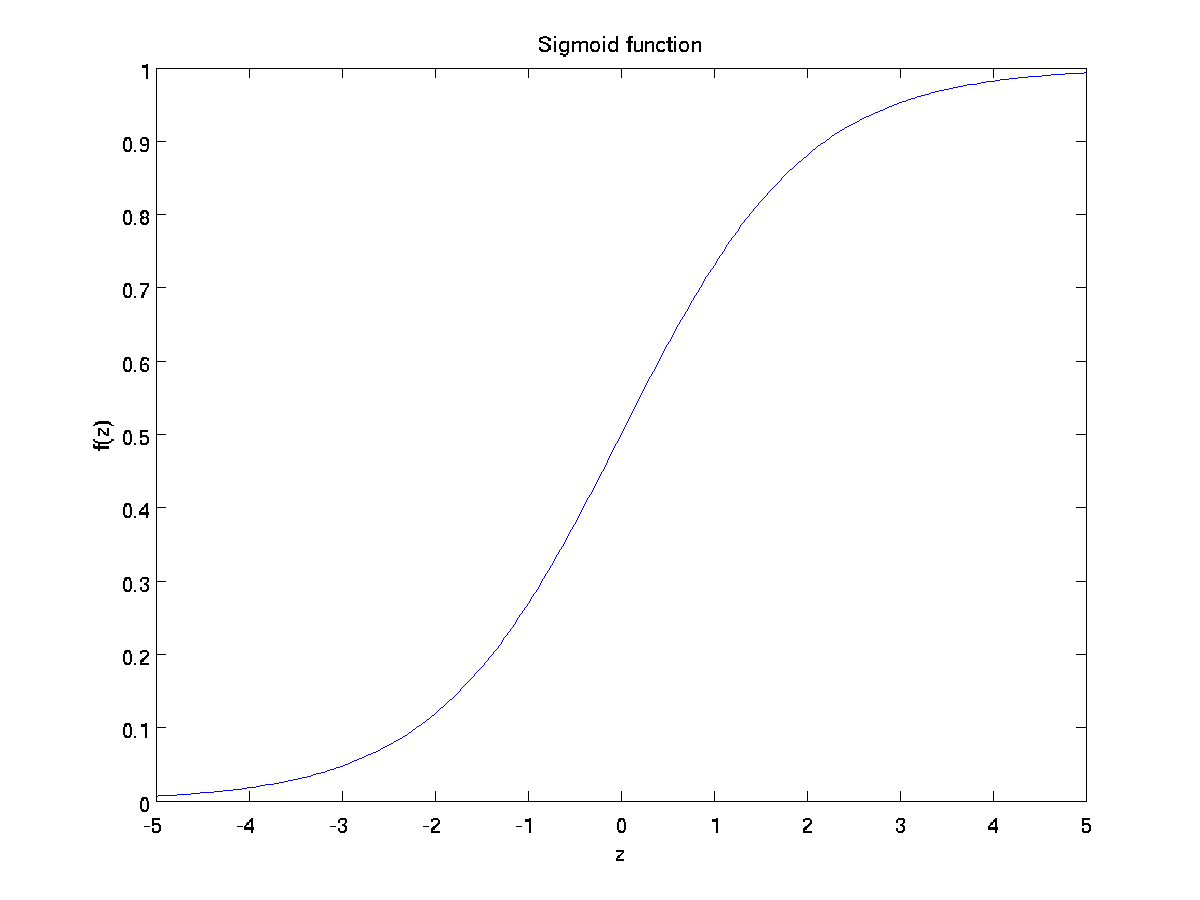
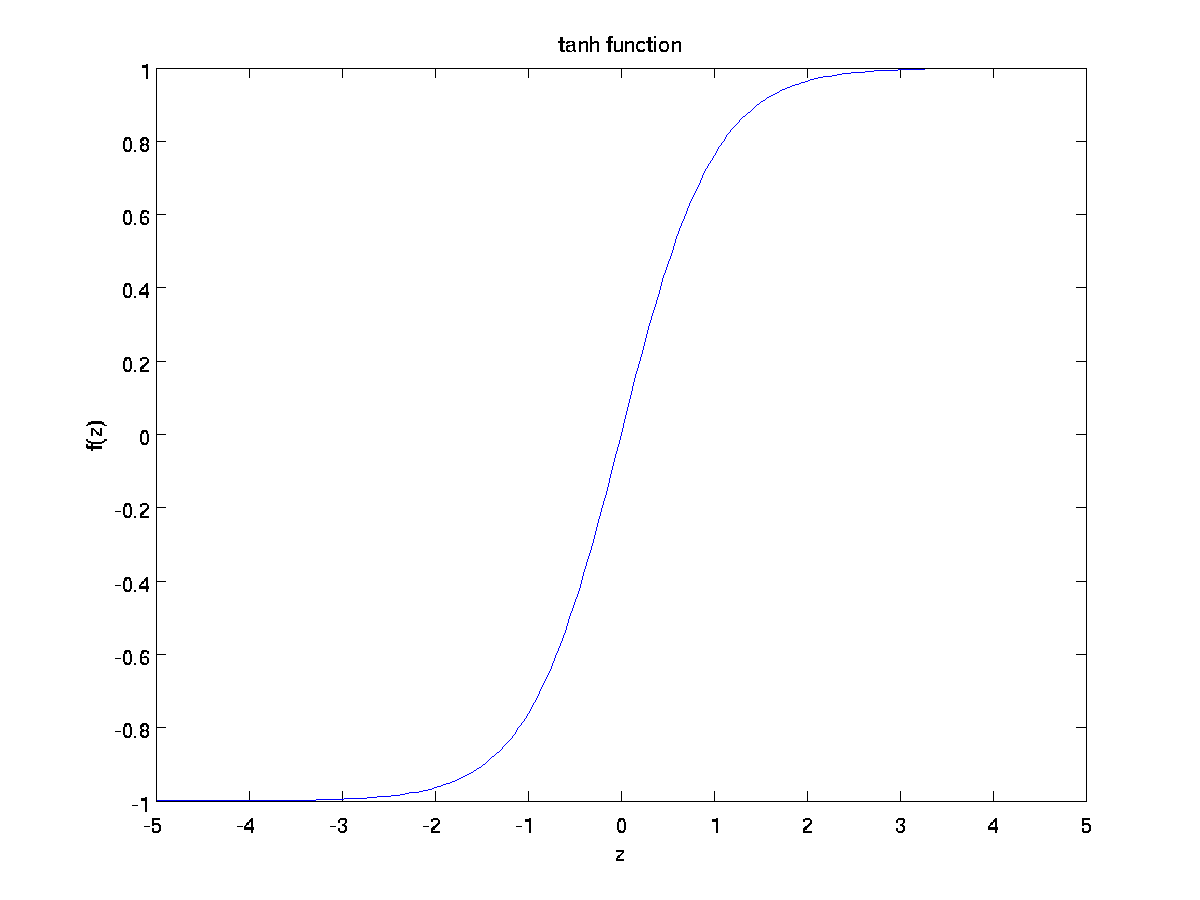
 tanh(z)函数式sigmoid函数的变体，它的输出范围是[−1,1]，而不是[ 0,1].

注意一个对后后面推导有用的等式：

对于sigmoid函数f(z) = 1 / (1 + exp( − z))，它的导函数为f'(z) = f(z)(1 − f(z)).

 

神经网络模型

神经网络就是把许多神经元连接到一起，使得一个神经元的输出作为另一个神经元的输入。下面是一个小规模的神经网络：

 

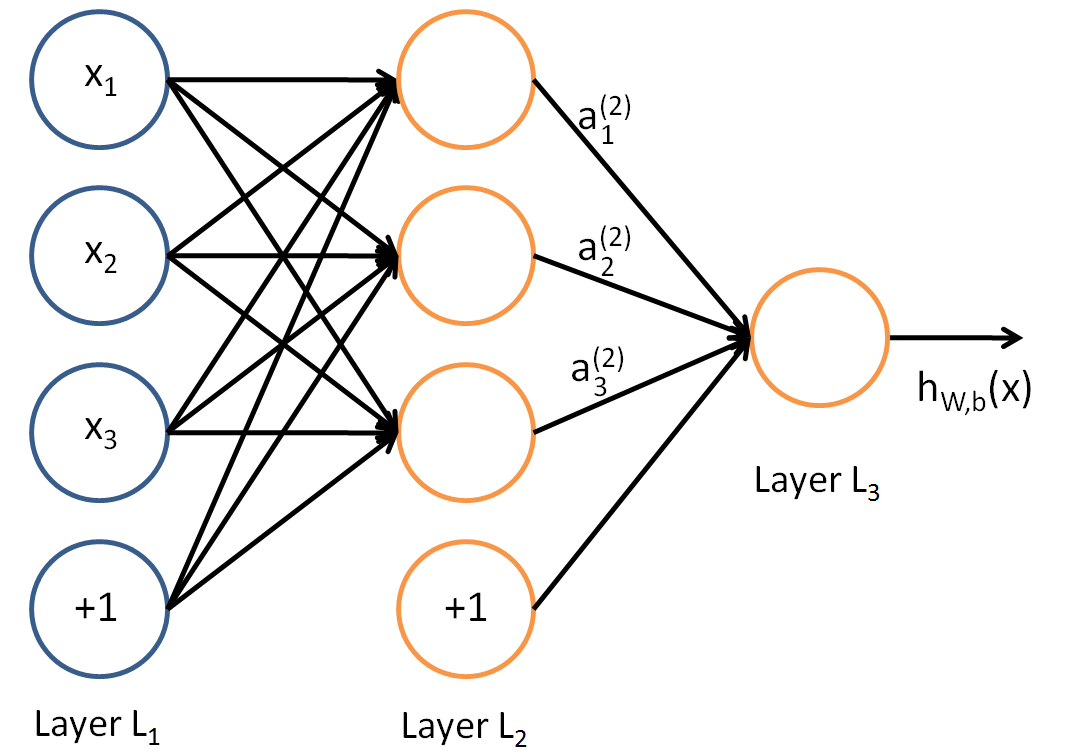
图中同样用圆圈表示神经网络的输入（蓝色的圆圈表示整个网络的输入，红色圆圈表示神经元），截距项为+1，但是这里称为偏置节点。网络的最左边的一层叫做输入层，最右边的一层叫做输出层（输出层可以有很多神经元节点，这个例子只有一个节点）。中间的一层称为隐层，因为它们的值在训练集中观察不到。可以说图中神经网络有3个输入节点（不包括偏置节点），3个隐层节点，1个输出节点。

用 nl  表示网络的层数，因此例子中 nl  = 3，用 Ll 代表 l 层，所以 L1 就是输入层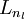，L_{n_l}  就是输出层。网络参数(W,b) = (W(1),b(1),W(2),b(2))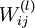，W^{(l)}_{ij} 表示 l 层的节点 j 与 l+1 层的节点 i 之间的连接权重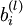，b^{(l)}_i  表示与 l+1 层的节点 i 连接的偏置，因此，在这个例子中 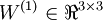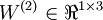W^{(1)} \in \Re^{3\times 3}，W^{(2)} \in \Re^{1\times 3}. 注意偏置节点是没有输入的，因为偏置节点输出总为+1. 用 sl  表示 l 层的节点数（不计偏置节点）。

用 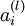a^{(l)}_i  表示 l 层的节点 i 的激活值（即输出值）。当 l = 1 时，用 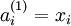a^{(1)}_i = x_i  表示第 i 个输入。给定参数 W,b, 神经网络的假设模型 hW,b(x) 输出一个实数。计算过程如下：

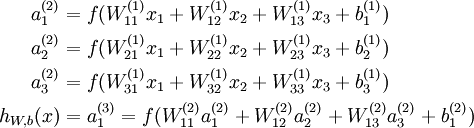
\begin{align} a_1^{(2)} &= f(W_{11}^{(1)}x_1 + W_{12}^{(1)} x_2 + W_{13}^{(1)} x_3 + b_1^{(1)}) \\ a_2^{(2)} &= f(W_{21}^{(1)}x_1 + W_{22}^{(1)} x_2 + W_{23}^{(1)} x_3 + b_2^{(1)}) \\ a_3^{(2)} &= f(W_{31}^{(1)}x_1 + W_{32}^{(1)} x_2 + W_{33}^{(1)} x_3 + b_3^{(1)}) \\ h_{W,b}(x) &= a_1^{(3)} = f(W_{11}^{(2)}a_1^{(2)} + W_{12}^{(2)} a_2^{(2)} + W_{13}^{(2)} a_3^{(2)} + b_1^{(2)}) \end{align}

 

接着用 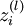z^{(l)}_i 表示 l 层的节点 i 的输入加权和（包括偏置节点），如：

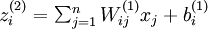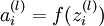\textstyle z_i^{(2)} = \sum_{j=1}^n W^{(1)}_{ij} x_j + b^{(1)}_i，所以 a^{(l)}_i = f(z^{(l)}_i).

于是上面计算过程的表示就可以更简洁地写为：

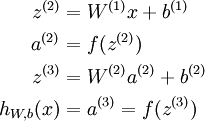
\begin{align} z^{(2)} &= W^{(1)} x + b^{(1)} \\ a^{(2)} &= f(z^{(2)}) \\ z^{(3)} &= W^{(2)} a^{(2)} + b^{(2)} \\ h_{W,b}(x) &= a^{(3)} = f(z^{(3)}) \end{align}

称这个过程为前向传播（forward propagation）.

更为一般的是，用 a(1) = x 表示输入层的值，于是 l 层的激活值就是 a(l) ，计算  l + 1 层的激活值 a(l + 1) ：

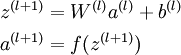
\begin{align} z^{(l+1)} &= W^{(l)} a^{(l)} + b^{(l)} \\ a^{(l+1)} &= f(z^{(l+1)}) \end{align}

把所有参数矩阵化，用矩阵—向量操作，可以利用线性代数的优势快速求解网络参数。

到目前为止，我们只关注了一个神经网络的例子，但是神经网络还有许多其它的结构（神经元之间的连接类型），包括多个隐层的神经网络。最常见的方式是，对于一个 nl  层的神经网络，第1层代表输入层，nl  层代表输出层，中间的每个 l 层与 l+1 层紧密相连。设置好以后，就可以像上述的前向反馈一样，逐层计算激活值，这就是一种前馈神经网络（feedforward neural network），因为连接中没有回路或者闭环。

神经网络可以有多个输出节点。这里给出一个含有2个隐层和2个输出节点的网络：

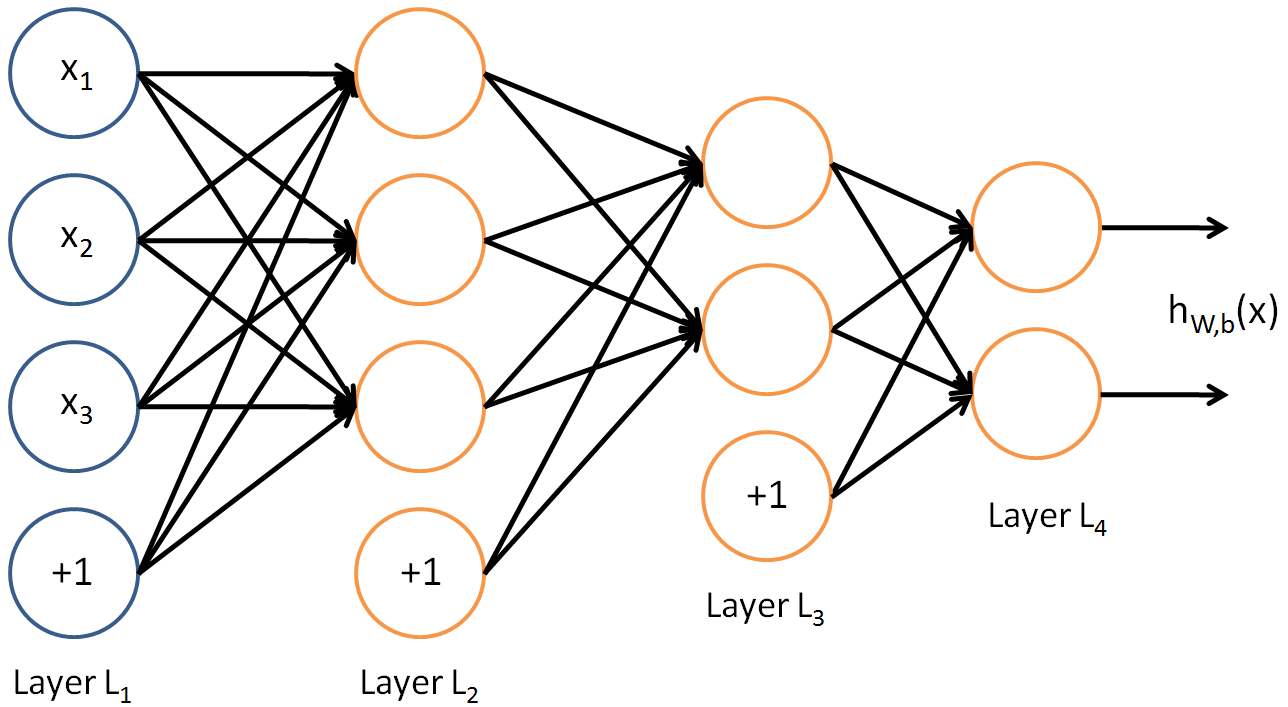
训练这个网络需要训练样本 (x(i),y(i)) 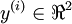，y^{(i)} \in \Re^2. 当你需要预测多个值得时候，这种网络会很有用。例如，在医疗诊断应用中，向量 x 给出一个病人的特征，不同的输出 yi 可能分别表示不同种类的疾病是否存在。

 

 

学习来源：http://deeplearning.stanford.edu/wiki/index.php/Neural_Networks

 

posted @ 2014-10-11 10:26  90Zeng  阅读(3533)  评论(0)  编辑  收藏  举报