稀疏自动编码之梯度检验
众所周知,反向传播算法很难调试和得到正确结果,特别是在执行过程中存在许多细小难以察觉的错误。这里介绍一种方法来确定代码中导数的计算是否正确。使用这里所述求导检验方法,可以帮助提升写正确代码的信心。
假设我们想最小化关于  的函数
的函数  . 对于这个例子,假设
. 对于这个例子,假设 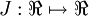 ,所以
,所以 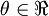 . 在一维空间,梯度下降的一次迭代公式如下:
. 在一维空间,梯度下降的一次迭代公式如下:
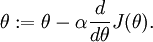
假设我们已经实现了某个函数 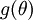 去计算
去计算 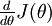 ,那么梯度下降时参数更新就可以这样:
,那么梯度下降时参数更新就可以这样: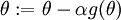 . 该如何检验我们编写的函数
. 该如何检验我们编写的函数 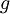 是正确的呢?
是正确的呢?
回忆导数的定义:
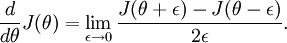
对于任意的  ,可以用如下公式来从数值上近似导数值:
,可以用如下公式来从数值上近似导数值:
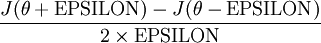
在实践中,将 EPSILON 设定为一个极小的常数,如 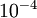 .(虽然EPSILON可以取得极其小的值,如
.(虽然EPSILON可以取得极其小的值,如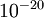 ,但这样会导致数值舍入误差),通常
,但这样会导致数值舍入误差),通常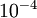 就足够了。
就足够了。
现在,给定假设中计算 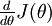 的函数
的函数 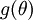 ,我们可以通过如下方式检验该函数的正确如否:
,我们可以通过如下方式检验该函数的正确如否:
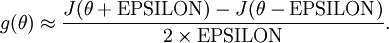
到底这两个值接近到什么样的一个程度才算正确呢?要取决于 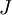 的具体形似。但是假定
的具体形似。但是假定 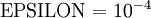 , 通常我们会发现上述式子左右两边的值至少有4位有效数字是一样的(甚至更多)。
, 通常我们会发现上述式子左右两边的值至少有4位有效数字是一样的(甚至更多)。
现在,考虑 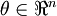 ,即参数是一个向量而不是一个实数(所以需要学习出
,即参数是一个向量而不是一个实数(所以需要学习出 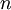 个参数),且
个参数),且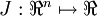 . 在我们的神经网络例子中使用符号
. 在我们的神经网络例子中使用符号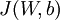 , 所以我们可以想象把这许多参数
, 所以我们可以想象把这许多参数 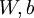 全部装进一个很长的向量
全部装进一个很长的向量  . 现在,就把导数检验过程泛化到
. 现在,就把导数检验过程泛化到  是向量的情况。
是向量的情况。
假设我们编写了一个函数 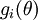 计算导数
计算导数 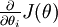 ,我们想要检验
,我们想要检验 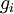 是否正确地计算出了导数值. 令
是否正确地计算出了导数值. 令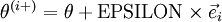 ,其中:
,其中:
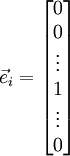
是第  个基向量(维数与
个基向量(维数与  一样,只有第
一样,只有第  个元素为1,其他位置元素全部为0).所以对于
个元素为1,其他位置元素全部为0).所以对于 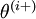 ,除了第
,除了第  个元素比
个元素比 的第
的第  个元素多加了EPSILON,其他元素完全一样。类似地有:
个元素多加了EPSILON,其他元素完全一样。类似地有: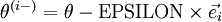 .然后就可以通过检查下面式子的正确与否来检验
.然后就可以通过检查下面式子的正确与否来检验 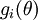 的正确性:
的正确性:
当用反向传播去训练神经网络时, 正确执行的算法可以得到:
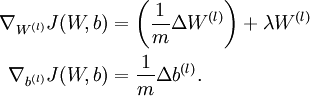
这展示在
稀疏自动编码之反向传播算法(BP)
的梯度下降伪代码中.通常用上面的方法计算出 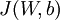 的导数值,通过它检验我们程序中
的导数值,通过它检验我们程序中 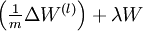 和
和 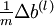 是否确实计算出了我们想要的到数值。
是否确实计算出了我们想要的到数值。
学习来源:http://deeplearning.stanford.edu/wiki/index.php/Gradient_checking_and_advanced_optimization


 浙公网安备 33010602011771号
浙公网安备 33010602011771号