Determining if a point lies on the interior of a polygon
Determining if a point lies on the interior of a polygon
Written by Paul Bourke November 1987
Solution 1 (2D)
The following is a simple solution to the problem often encountered in computer graphics, determining whether or not a point (x,y) lies inside or outside a 2D polygonally bounded plane. This is necessary for example in applications such as polygon filling on raster devices, hatching in drafting software, and determining the intersection of multiple polygons.
Consider a polygon made up of N vertices (xi,yi) where i ranges from 0 to N-1. The last vertex (xN,yN) is assumed to be the same as the first vertex (x0,y0), that is, the polygon is closed. To determine the status of a point (xp,yp) consider a horizontal ray emanating from (xp,yp) and to the right. If the number of times this ray intersects the line segments making up the polygon is even then the point is outside the polygon. Whereas if the number of intersections is odd then the point (xp,yp) lies inside the polygon. The following shows the ray for some sample points and should make the technique clear.
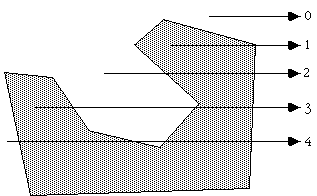
Note: for the purposes of this discussion 0 will be considered even, the test for even or odd will be based on modulus 2, that is, if the number of intersections modulus 2 is 0 then the number is even, if it is 1 then it is odd.
The only trick is what happens in the special cases when an edge or vertex of the polygon lies on the ray from (xp,yp). The possible situations are illustrated below.
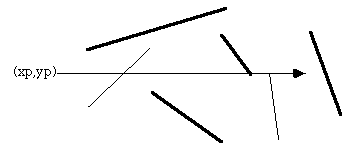
The thick lines above are not considered as valid intersections, the thin lines do count as intersections. Ignoring the case of an edge lying along the ray or an edge ending on the ray ensures that the endpoints are only counted once.
Note that this algorithm also works for polygons with holes as illustrated below
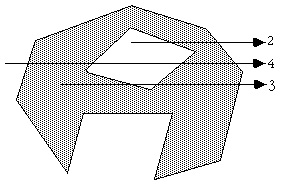
The following C function returns INSIDE or OUTSIDE indicating the status of a point P with respect to a polygon with N points.
#define MIN(x,y) (x < y ? x : y)
#define MAX(x,y) (x > y ? x : y)
#define INSIDE 0
#define OUTSIDE 1
typedef struct {
double x,y;
} Point;
int InsidePolygon(Point *polygon,int N,Point p)
{
int counter = 0;
int i;
double xinters;
Point p1,p2;
p1 = polygon[0];
for (i=1;i<=N;i++) {
p2 = polygon[i % N];
if (p.y > MIN(p1.y,p2.y)) {
if (p.y <= MAX(p1.y,p2.y)) {
if (p.x <= MAX(p1.x,p2.x)) {
if (p1.y != p2.y) {
xinters = (p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x;
if (p1.x == p2.x || p.x <= xinters)
counter++;
}
}
}
}
p1 = p2;
}
if (counter % 2 == 0)
return(OUTSIDE);
else
return(INSIDE);
}
The following code is by Randolph Franklin, it returns 1 for interior points and 0 for exterior points.
int pnpoly(int npol, float *xp, float *yp, float x, float y)
{
int i, j, c = 0;
for (i = 0, j = npol-1; i < npol; j = i++) {
if ((((yp[i] <= y) && (y < yp[j])) ||
((yp[j] <= y) && (y < yp[i]))) &&
(x < (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i]))
c = !c;
}
return c;
}
Contribution by Alexander Motrichuk:
//SOLUTION #1 (2D) - Redesigned #define MIN(x,y) (x < y ? x : y) #define MAX(x,y) (x > y ? x : y) #define INSIDE 1 #define OUTSIDE 0 struct Point { Point() : x(.0), y(.0) {}; Point(double x1, double y1) : x(x1), y(y1) {}; bool operator==(const Point& _right) { return x == _right.x && y == _right.y; }; double x, y; }; //horizintal left cross over direction algorithm //----------------------------------------------- // bound | value that will be returned only if (p) lies on the bound or vertex int InsidePolygon(Point* polygon, int N, Point p, int bound) { //cross points count of x int __count = 0; //neighbour bound vertices Point p1, p2; //left vertex p1 = polygon[0]; //check all rays for(int i = 1; i <= N; ++i) { //point is an vertex if(p == p1) return bound; //right vertex p2 = polygon[i % N]; //ray is outside of our interests if(p.y < MIN(p1.y, p2.y) || p.y > MAX(p1.y, p2.y)) { //next ray left point p1 = p2; continue; } //ray is crossing over by the algorithm (common part of) if(p.y > MIN(p1.y, p2.y) && p.y < MAX(p1.y, p2.y)) { //x is before of ray if(p.x <= MAX(p1.x, p2.x)) { //overlies on a horizontal ray if(p1.y == p2.y && p.x >= MIN(p1.x, p2.x)) return bound; //ray is vertical if(p1.x == p2.x) { //overlies on a ray if(p1.x == p.x) return bound; //before ray else ++__count; } //cross point on the left side else { //cross point of x double xinters = (p.y - p1.y) * (p2.x - p1.x) / (p2.y - p1.y) + p1.x; //overlies on a ray if(fabs(p.x - xinters) < __DBL_EPSILON__) return bound; //before ray if(p.x < xinters) ++__count; } } } //special case when ray is crossing through the vertex else { //p crossing over p2 if(p.y == p2.y && p.x <= p2.x) { //next vertex const Point& p3 = polygon[(i+1) % N]; //p.y lies between p1.y & p3.y if(p.y >= MIN(p1.y, p3.y) && p.y <= MAX(p1.y, p3.y)) { ++__count; } else { __count += 2; } } } //next ray left point p1 = p2; } //EVEN if(__count % 2 == 0) return(OUTSIDE); //ODD else return(INSIDE); }
Quote: "For most of the algorithms above there is a pathological case if the point being queried lies exactly on a vertex. The easiest way to cope with this is to test that as a separate process and make your own decision as to whether you want to consider them inside or outside."
Contribution in VBA by Giuseppe Iaria:
'--------------------------------------------------------------------------------------------------------- '************************************ Function InsidePolygon ************************************* '--------------------------------------------------------------------------------------------------------- 'VBA implementation of the theory provided by Paul Bourke (http://paulbourke.net/geometry/polygonmesh/) 'author: ing. Giuseppe Iaria - rev. 20/08/2014 '--------------------------------------------------------------------------------------------------------- 'The function is based on Solution 1 (2D) 'The function determines if a point P lies inside or outside a Polygon, returning "True" or "False" 'The points are defined through the user-defined type "Point" 'The Polygon is an array of points, each being a user-defined type "Point" 'The Polygon is implemented assuming a "Base 1" condition, so the "Option Base 1" statement is required 'The optional argument "OnPolygonBorder" deals with these special cases: ' - P lies on a vertex of the Polygon ' - P lies on a line segment of the Polygon 'If omitted or passed as "False", and a special case occurs, then the function returns "False" 'If passed as "True", and a special case occurs, then the function returns "True" 'Auxiliary functions used: ' - DistancePointSegment: determines the distance between a point and a line segment ' - Distance2Point: determines the distance between two points 'Both the auxiliary functions have been developed on: ' - the theory by Paul Bourke (http://paulbourke.net/geometry/pointlineplane/) ' - an original VBA code by Brandon Crosby (http://paulbourke.net/geometry/pointlineplane/source.vba) '--------------------------------------------------------------------------------------------------------- Option Base 1 Public Type Point x As Double y As Double End Type Public Function InsidePolygon(Polygon() As Point, P As Point, Optional ByVal OnPolygonBorder As Boolean) As Boolean Dim counter As Integer, i As Integer, ip1 As Integer Dim xInters As Double, dist As Double Const EPS As Single = 0.0001 'Check if the point lies on a polygon's vertex or line segment For i = 1 To UBound(Polygon) ip1 = i Mod UBound(Polygon) + 1 dist = DistancePointSegment(P, Polygon(i), Polygon(ip1)) If dist < EPS Then If OnPolygonBorder Then InsidePolygon = True Else InsidePolygon = False End If Exit Function End If Next i 'Determine the numbers of intersection between the orizzontal ray from point and polygon For i = 1 To UBound(Polygon) ip1 = i Mod UBound(Polygon) + 1 If P.y > IIf(Polygon(i).y < Polygon(ip1).y, Polygon(i).y, Polygon(ip1).y) Then If P.y <= IIf(Polygon(i).y > Polygon(ip1).y, Polygon(i).y, Polygon(ip1).y) Then If P.x <= IIf(Polygon(i).x > Polygon(ip1).x, Polygon(i).x, Polygon(ip1).x) Then If Polygon(i).y <> Polygon(ip1).y Then xInters = Polygon(i).x + (Polygon(ip1).x - Polygon(i).x) * (P.y - Polygon(i).y) / (Polygon(ip1).y - Polygon(i).y) If (Polygon(i).x = Polygon(ip1).x) Or (P.x <= xInters) Then counter = counter + 1 End If End If End If End If Next i If counter Mod 2 = 0 Then InsidePolygon = False Else InsidePolygon = True End Function Private Function DistancePointSegment(P As Point, P1 As Point, P2 As Point) As Double Dim LineMag As Double, u As Double Dim d1 As Double, d2 As Double Dim Pint As Point Const EPS As Single = 0.0001 LineMag = Distance2Point(P1, P2) If LineMag < EPS Then Exit Function u = (((P.x - P1.x) * (P2.x - P1.x)) + ((P.y - P1.y) * (P2.y - P1.y))) / LineMag ^ 2 If u < 0 Or u > 1 Then d1 = Distance2Point(P, P1) d2 = Distance2Point(P, P2) If d1 > d2 Then DistancePointSegment = d2 Else DistancePointSegment = d1 Else Pint.x = P1.x + u * (P2.x - P1.x) Pint.y = P1.y + u * (P2.y - P1.y) DistancePointSegment = Distance2Point(P, Pint) End If End Function Private Function Distance2Point(P1 As Point, P2 As Point) As Double Distance2Point = Sqr((P2.x - P1.x) ^ 2 + (P2.y - P1.y) ^ 2) End Function
Contribution written in c# by Jerry Knauss:
public static bool Contains( Point[] points, Point p ) { bool result = false; for( int i = 0; i < points.Length - 1; i++ ) { if( ( ( ( points[ i + 1 ].Y <= p.Y ) && ( p.Y < points[ i ].Y ) ) || ( ( points[ i ].Y <= p.Y ) && ( p.Y < points[ i + 1 ].Y ) ) ) && ( p.X < ( points[ i ].X - points[ i + 1 ].X ) * ( p.Y - points[ i + 1 ].Y ) / ( points[ i ].Y - points[ i + 1 ].Y ) + points[ i + 1 ].X ) ) { result = !result; } } return result; }
Solution 2 (2D)
Another solution forwarded by Philippe Reverdy is to compute the sum of the angles made between the test point and each pair of points making up the polygon. If this sum is 2pi then the point is an interior point, if 0 then the point is an exterior point. This also works for polygons with holes given the polygon is defined with a path made up of coincident edges into and out of the hole as is common practice in many CAD packages.
The inside/outside test might then be defined in C as
typedef struct {
int h,v;
} Point;
int InsidePolygon(Point *polygon,int n,Point p)
{
int i;
double angle=0;
Point p1,p2;
for (i=0;i<n;i++) {
p1.h = polygon[i].h - p.h;
p1.v = polygon[i].v - p.v;
p2.h = polygon[(i+1)%n].h - p.h;
p2.v = polygon[(i+1)%n].v - p.v;
angle += Angle2D(p1.h,p1.v,p2.h,p2.v);
}
if (ABS(angle) < PI)
return(FALSE);
else
return(TRUE);
}
/*
Return the angle between two vectors on a plane
The angle is from vector 1 to vector 2, positive anticlockwise
The result is between -pi -> pi
*/
double Angle2D(double x1, double y1, double x2, double y2)
{
double dtheta,theta1,theta2;
theta1 = atan2(y1,x1);
theta2 = atan2(y2,x2);
dtheta = theta2 - theta1;
while (dtheta > PI)
dtheta -= TWOPI;
while (dtheta < -PI)
dtheta += TWOPI;
return(dtheta);
}
Solution 3 (2D)
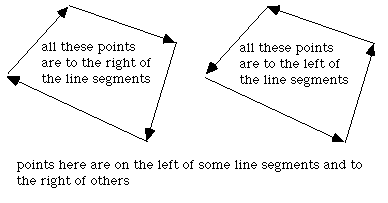
There are other solutions to this problem for polygons with special attributes. If the polygon is convex then one can consider the polygon as a "path" from the first vertex. A point is on the interior of this polygons if it is always on the same side of all the line segments making up the path.
Given a line segment between P0 (x0,y0) and P1 (x1,y1), another point P (x,y) has the following relationship to the line segment.
Compute
if it is less than 0 then P is to the right of the line segment, if greater than 0 it is to the left, if equal to 0 then it lies on the line segment.
Solution 4 (3D)
|
This solution was motivated by solution 2 and correspondence with Reinier van Vliet and Remco Lam. To determine whether a point is on the interior of a convex polygon in 3D one might be tempted to first determine whether the point is on the plane, then determine it's interior status. Both of these can be accomplished at once by computing the sum of the angles between the test point (q below) and every pair of edge points p[i]->p[i+1]. This sum will only be 2pi if both the point is on the plane of the polygon AND on the interior. The angle sum will tend to 0 the further away from the polygon point q becomes. |
 |
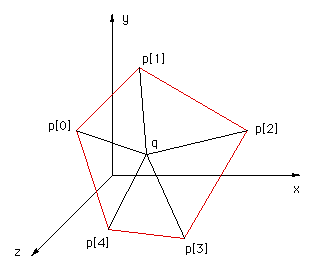The following code snippet returns the angle sum between the test point q and all the vertex pairs. Note that the angle sum is returned in radians.
typedef struct {
double x,y,z;
} XYZ;
#define EPSILON 0.0000001
#define MODULUS(p) (sqrt(p.x*p.x + p.y*p.y + p.z*p.z))
#define TWOPI 6.283185307179586476925287
#define RTOD 57.2957795
double CalcAngleSum(XYZ q,XYZ *p,int n)
{
int i;
double m1,m2;
double anglesum=0,costheta;
XYZ p1,p2;
for (i=0;i<n;i++) {
p1.x = p[i].x - q.x;
p1.y = p[i].y - q.y;
p1.z = p[i].z - q.z;
p2.x = p[(i+1)%n].x - q.x;
p2.y = p[(i+1)%n].y - q.y;
p2.z = p[(i+1)%n].z - q.z;
m1 = MODULUS(p1);
m2 = MODULUS(p2);
if (m1*m2 <= EPSILON)
return(TWOPI); /* We are on a node, consider this inside */
else
costheta = (p1.x*p2.x + p1.y*p2.y + p1.z*p2.z) / (m1*m2);
anglesum += acos(costheta);
}
return(anglesum);
}
Note
For most of the algorithms above there is a pathological case if the point being queries lies exactly on a vertex. The easiest way to cope with this is to test that as a separate process and make your own decision as to whether you want to consider them inside or outside.
本文来自博客园，作者：古道轻风，转载请注明原文链接：https://www.cnblogs.com/88223100/p/Determining_if_a_point_lies_on_the_interior_of_a_polygon.html
