【模版】分治法求平面最近点对
这篇博文非原创,文章摘自lishuhuakai大佬,蒟蒻只是配个代码,加点注释。
在应用中,常用诸如点、圆等简单的几何对象代表现实世界中的实体。在涉及这些几何对象的问题中,常需要了解其邻域中其他几何对象的信息。例如,在空中交通控制问题中,若将飞机作为空间中移动的一个点来看待,则具有最大碰撞危险的2架飞机,就是这个空间中最接近的一对点。这类问题是计算几何学中研究的基本问题之一。下面我们着重考虑平面上的最接近点对问题。
最接近点对问题的提法是:给定平面上n个点,找其中的一对点,使得在n个点的所有点对中,该点对的距离最小。
严格地说,最接近点对可能多于1对。为了简单起见,这里只限于找其中的一对。
参考解答
这个问题很容易理解,似乎也不难解决。我们只要将每一点与其他n-1个点的距离算出,找出达到最小距离的两个点即可。然而,这样做效率太低,需要O(n2)的计算时间。在问题的计算复杂性中我们可以看到,该问题的计算时间下界为Ω(nlogn)。这个下界引导我们去找问题的一个θ(nlogn)算法。
这个问题显然满足分治法的第一个和第二个适用条件,我们考虑将所给的平面上n个点的集合S分成2个子集S1和S2,每个子集中约有n/2个点,·然后在每个子集中递归地求其最接近的点对。在这里,一个关键的问题是如何实现分治法中的合并步骤,即由S1和S2的最接近点对,如何求得原集合S中的最接近点对,因为S1和S2的最接近点对未必就是S的最接近点对。如果组成S的最接近点对的2个点都在S1中或都在S2中,则问题很容易解决。但是,如果这2个点分别在S1和S2中,则对于S1中任一点p,S2中最多只有n/2个点与它构成最接近点对的候选者,仍需做n2/4次计算和比较才能确定S的最接近点对。因此,依此思路,合并步骤耗时为O(n2)。整个算法所需计算时间T(n)应满足:
T(n)=2T(n/2)+O(n2)
它的解为T(n)=O(n2),即与合并步骤的耗时同阶,显示不出比用穷举的方法好。从解递归方程的套用公式法,我们看到问题出在合并步骤耗时太多。这启发我们把注意力放在合并步骤上。
为了使问题易于理解和分析,我们先来考虑一维的情形。此时S中的n个点退化为x轴上的n个实数x1,x2,..,xn。最接近点对即为这n个实数中相差最小的2个实数。我们显然可以先将x1,x2,..,xn排好序,然后,用一次线性扫描就可以找出最接近点对。这种方法主要计算时间花在排序上,因此如在排序算法中所证明的,耗时为O(nlogn)。然而这种方法无法直接推广到二维的情形。因此,对这种一维的简单情形,我们还是尝试用分治法来求解,并希望能推广到二维的情形。
假设我们用x轴上某个点m将S划分为2个子集S1和S2,使得S1={x∈S|x≤m};S2={x∈S|x>m}。这样一来,对于所有p∈S1和q∈S2有p
递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2},并设δ=min{|p1-p2|,|q1-q2|},S中的最接近点对或者是{p1,p2},或者是{q1,q2},或者是某个{p3,q3},其中p3∈S1且q3∈S2。如图1所示。
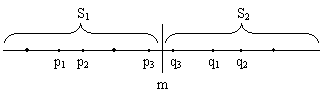 图1 一维情形的分治法
图1 一维情形的分治法
我们注意到,如果S的最接近点对是{p3,q3},即|p3-q3|<δ,则p3和q3两者与m的距离不超过δ,即|p3-m|<δ,|q3-m|<δ,也就是说,p3∈(m-δ,m],q3∈(m,m+δ]。由于在S1中,每个长度为δ的半闭区间至多包含一个点(否则必有两点距离小于δ),并且m是S1和S2的分割点,因此(m-δ,m]中至多包含S中的一个点。同理,(m,m+δ]中也至多包含S中的一个点。由图1可以看出,如果(m-δ,m]中有S中的点,则此点就是S1中最大点。同理,如果(m,m+δ]中有S中的点,则此点就是S2中最小点。因此,我们用线性时间就能找到区间(m-δ,m]和(m,m+δ]中所有点,即p3和q3。从而我们用线性时间就可以将S1的解和S2的解合并成为S的解。也就是说,按这种分治策略,合并步可在O(n)时间内完成。这样是否就可以得到一个有效的算法了呢?还有一个问题需要认真考虑,即分割点m的选取,及S1和S2的划分。选取分割点m的一个基本要求是由此导出集合S的一个线性分割,即S=S1∪S2 ,S1∩S2=Φ,且S1{x|x≤m};S2{x|x>m}。容易看出,如果选取m=[max(S)+min(S)]/2,可以满足线性分割的要求。选取分割点后,再用O(n)时间即可将S划分成S1={x∈S|x≤m}和S2={x∈S|x>m}。然而,这样选取分割点m,有可能造成划分出的子集S1和S2的不平衡。例如在最坏情况下,|S1|=1,|S2|=n-1,由此产生的分治法在最坏情况下所需的计算时间T(n)应满足递归方程:
T(n)=T(n-1)+O(n)
它的解是T(n)=O(n2)。这种效率降低的现象可以通过分治法中"平衡子问题"的方法加以解决。也就是说,我们可以通过适当选择分割点m,使S1和S2中有大致相等个数的点。自然地,我们会想到用S的n个点的坐标的中位数来作分割点。在选择算法中介绍的选取中位数的线性时间算法使我们可以在O(n)时间内确定一个平衡的分割点m。
由以上的分析可知,该算法的分割步骤和合并步骤总共耗时O(n)。因此,算法耗费的计算时间T(n)满足递归方程:
解此递归方程可得T(n)=O(nlogn)。
这个算法看上去比用排序加扫描的算法复杂,然而这个算法可以向二维推广。
下面我们来考虑二维的情形。此时S中的点为平面上的点,它们都有2个坐标值x和y。为了将平面上点集S线性分割为大小大致相等的2个子集S1和S2,我们选取一垂直线l:x=m来作为分割直线。其中m为S中各点x坐标的中位数。由此将S分割为S1={p∈S|px≤m}和S2={p∈S|px>m}。从而使S1和S2分别位于直线l的左侧和右侧,且S=S1∪S2 。由于m是S中各点x坐标值的中位数,因此S1和S2中的点数大致相等。
递归地在S1和S2上解最接近点对问题,我们分别得到S1和S2中的最小距离δ1和δ2。现设δ=min(δ1,δ1)。若S的最接近点对(p,q)之间的距离d(p,q)<δ则p和q必分属于S1和S2。不妨设p∈S1,q∈S2。那么p和q距直线l的距离均小于δ。因此,我们若用P1和P2分别表示直线l的左边和右边的宽为δ的2个垂直长条,则p∈P1,q∈P2,如图2所示。
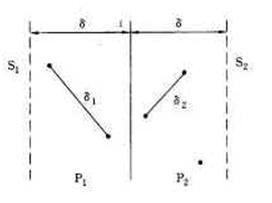
图2 距直线l的距离小于δ的所有点
在一维的情形,距分割点距离为δ的2个区间(m-δ,m](m,m+δ]中最多各有S中一个点。因而这2点成为唯一的末检查过的最接近点对候选者。二维的情形则要复杂些,此时,P1中所有点与P2中所有点构成的点对均为最接近点对的候选者。在最坏情况下有n2/4对这样的候选者。但是P1和P2中的点具有以下的稀疏性质,它使我们不必检查所有这n2/4对候选者。考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有d(p,q)<δ。满足这个条件的P2中的点有多少个呢?容易看出这样的点一定落在一个δ×2δ的矩形R中,如图3所示。
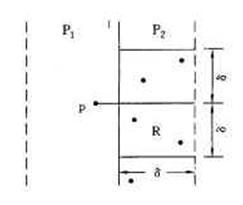 图3 包含点q的δ×2δ的矩形R
图3 包含点q的δ×2δ的矩形R
由δ的意义可知P2中任何2个S中的点的距离都不小于δ。由此可以推出矩形R中最多只有6个S中的点。事实上,我们可以将矩形R的长为2δ的边3等分,将它的长为δ的边2等分,由此导出6个(δ/2)×(2δ/3)的矩形。如图4(a)所示。
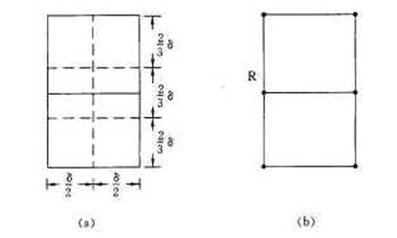 图4 矩形R中点的稀疏性
图4 矩形R中点的稀疏性
若矩形R中有多于6个S中的点,则由鸽舍原理易知至少有一个δ×2δ的小矩形中有2个以上S中的点。设u,v是这样2个点,它们位于同一小矩形中,则
因此d(u,v)≤5δ/6<δ 。这与δ的意义相矛盾。也就是说矩形R中最多只有6个S中的点。图4(b)是矩形R中含有S中的6个点的极端情形。由于这种稀疏性质,对于P1中任一点p,P2中最多只有6个点与它构成最接近点对的候选者。因此,在分治法的合并步骤中,我们最多只需要检查6×n/2=3n对候选者,而不是n2/4对候选者。这是否就意味着我们可以在O(n)时间内完成分治法的合并步骤呢?现在还不能作出这个结论,因为我们只知道对于P1中每个S1中的点p最多只需要检查P2中的6个点,但是我们并不确切地知道要检查哪6个点。为了解决这个问题,我们可以将p和P2中所有S2的点投影到垂直线l上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中,所以它们在直线l上的投影点距p在l上投影点的距离小于δ。由上面的分析可知,这种投影点最多只有6个。因此,若将P1和P2中所有S的点按其y坐标排好序,则对P1中所有点p,对排好序的点列作一次扫描,就可以找出所有最接近点对的候选者,对P1中每一点最多只要检查P2中排好序的相继6个点。
下面我们来分析一下算法CPAIR2的计算复杂性。设对于n个点的平面点集S,算法耗时T(n)。算法的第1步和第5步用了O(n)时间,第3步和第6步用了常数时间,第2步用了2T(n/2)时间。若在每次执行第4步时进行排序,则在最坏情况下第4步要用O(nlogn)时间。这不符合我们的要求。因此,在这里我们要作一个技术上的处理。我们采用设计算法时常用的预排序技术,即在使用分治法之前,预先将S中n个点依其y坐标值排好序,设排好序的点列为P。在执行分治法的第4步时,只要对P作一次线性扫描,即可抽取出我们所需要的排好序的点列P1和P2。然后,在第5步中再对P1*作一次线性扫描,即可求得δl。因此,第4步和第5步的两遍扫描合在一起只要用O(n)时间。这样一来,经过预排序处理后的算法CPAIR2所需的计算时间T(n)满足递归方程:
显而易见T(n)=O(nlogn),预排序所需的计算时间为O(n1ogn)。因此,整个算法所需的计算时间为O(nlogn)。在渐近的意义下,此算法已是最优的了。
不得不说写的太好了通俗易懂,从一维的最近点对推广到二维的最近点对,算法复杂度也证明的很清晰。
我太懒了就直接配几道例题吧:
这是配的代码:
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
#include<set>
#define ll long long
#define db double
#define midd int mid=(l+r)>>1
#define rg register int
using namespace std;
const db inf=1e16;
struct su{
db x,y;
}a[200005],b[200005];
int n;
inline int qr(){//快读
char ch;
while((ch=getchar())<'0'||ch>'9');
int res=ch^48;
while((ch=getchar())>='0'&&ch<='9')
res=res*10+(ch^48);
return res;
}
inline db min(db x,db y){return x>y?y:x;}
inline bool cmp_x(su x,su y){return x.x<y.x;}
inline bool cmp_y(su x,su y){return x.y<y.y;}
inline db dis(su x,su y){return pow((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y),0.5);}
inline db find(int l,int r){
if(l>=r)return inf; //特判
if(l+1==r)return dis(a[l],a[r]);
midd; db d=min(find(l,mid),find(mid+1,r));//二分区间
int t=0,sl=mid,sr=mid;
while(a[sl].x+d>a[mid].x&&sl>=l)--sl;//从中间想左边延伸d的长度
while(a[sr].x-d<a[mid].x&&sr<=r)++sr;//从中间想右边延伸d的长度
++sl;--sr; // 注意一下
for(rg i=sl;i<=sr;++i)b[++t]=a[i];//搬过来
sort(b+1,b+t+1,cmp_y); //按y值排序
for(rg i=1;i<=t;++i)
for(rg j=i+1;j<=t;++j)
if(b[j].y-b[i].y>=d)break;//与当前点超过此长度的点不会再更新答案了
else d=min(d,dis(b[i],b[j]));//更新答案
return d;//向上回溯
}
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=qr();
for(rg i=1;i<=n;++i)
a[i].x=qr(),a[i].y=qr();
sort(a+1,a+n+1,cmp_x);//先按x值排序
printf("%.4lf\n",find(1,n));
return 0;
}
注:虽然归并排序在二分答案中往往有优势(随着区间分治可以在当下\(O(n)\)排出来,具体看代码),但博主还是很执着的使用了快排。但仔细想一下,其实快排也有优势的:归并会对整个区间\(O(n)\)排序,但是如果用快排我们只需要将和中间点距离不超过\(d\) 的点排序,虽然复杂度为\(O(nlogn)\),而且实际速度也跑不过归并,但我们也只落后了几十毫秒而已的。
归并版平面最近点对:(kuai了某压行神犇gql的代码):
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register
#define ll long long
#define lf double
#define gc getchar()
#define rp(i,x,y) for(rg ll i=x;i<=y;++i)
#define my(i,x,y) for(rg ll i=x;i>=y;--i)
const ll N=200000+10;const lf inf=(lf)1000000000000000000,eps=0.00000001;
ll n;
struct node{ll x,y;}nod[N],tmp[N];
il ll read()
{
rg char ch=gc;rg ll x=0;rg bool y=1;
while(ch!='-' && (ch>'9' || ch<'0'))ch=gc;
if(ch=='-')ch=gc,y=0;
while(ch>='0' && ch<='9')x=(x<<1)+(x<<3)+(ch^'0'),ch=gc;
return y?x:-x;
}
il bool cmp(node gd,node gs){return gd.x<gs.x;}
il bool cmq(node gd,node gs){return gd.y<gs.y;}
il lf dis(node gd,node gs){return sqrt((gd.x-gs.x)*(gd.x-gs.x)+(gd.y-gs.y)*(gd.y-gs.y));}
il lf min(lf gd,lf gs){return gd<gs?gd:gs;}
il lf solv(ll x,ll y)
{
if(x>=y)return inf;
ll mid=(x+y)>>1,i=x,j=mid+1,head=1,tail=0,k=x;double midline=(double)(nod[mid].x+nod[mid+1].x)/2,as,d;as=d=min(solv(x,mid),solv(mid+1,y));
while(i<=mid && j<=y)if(cmq(nod[i],nod[j]))tmp[k]=nod[i],++i,++k;else tmp[k]=nod[j],++j,++k;
if(i<=mid)while(i<=mid)tmp[k]=nod[i],++i,++k;else while(j<=y)tmp[k]=nod[j],++j,++k;
rp(i,x,y)nod[i]=tmp[i];
if(y==x+1)return dis(nod[x],nod[x+1]);
rp(i,x,y)
if(fabs(nod[i].x-midline)<=d+eps)
{
while(head<=tail && nod[i].y-tmp[head].y>=d)++head;
rp(j,head,tail)as=min(as,dis(nod[i],tmp[j]));
tmp[++tail]=nod[i];
}
return as;
}
int main()
{
// freopen("math.in","r",stdin);freopen("math.out","w",stdout);
n=read();rp(i,1,n)nod[i].x=read(),nod[i].y=read();sort(nod+1,nod+1+n,cmp);printf("%.4f",solv(1,n));
return 0;
}

