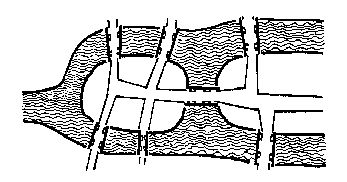
哥尼斯堡是位于普累格河上的一座城市,它包含两个岛屿及连接它们的七座桥,如下图所示。
可否走过这样的七座桥,而且每桥只走过一次?瑞士数学家欧拉(Leonhard Euler,1707—1783)最终解决了这个问题,并由此创立了拓扑学。
这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面,可画过图中每条边仅一次,且可以回到起点的一条回路。现给定一个无向图,问是否存在欧拉回路?
输入格式:
输入第一行给出两个正整数,分别是节点数N (1≤N≤1000)和边数M;随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个节点的编号(节点从1到N编号)。
输出格式:
若欧拉回路存在则输出1,否则输出0。
输入样例1:
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6
输出样例1:
1
输入样例2:
5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4
输出样例2:
0
判断是不是欧拉回路,还记得什么是欧拉回路吗,连通图,不存在奇数顶点,要通过所有边一次且仅仅一次行遍所有顶点才叫欧拉图。学离散果然有用。
代码:
#include <stdio.h> #include <stdlib.h> #include <string.h> #define inf 999999999 int n,m,flag = 0; int e[1001][1001]; int vis[1001]; int degree[1001]; void dfs(int s,int c) { if(flag)return; if(c == n) { flag = 1; return; } for(int i = 1;i <= n;i ++) { if(vis[i] || e[s][i] == 0)continue; vis[i] = 1; dfs(i,c + 1); vis[i] = 0; } } int check() { for(int i = 1;i <= n;i ++) if(degree[i]%2)return 0; return 1; } int main() { int a,b; scanf("%d%d",&n,&m); for(int i = 0;i < m;i ++) { scanf("%d%d",&a,&b); e[a][b] = e[b][a] = 1; degree[a] ++; degree[b] ++; } vis[1] = 1; dfs(1,1); if(flag&&check())printf("1"); else printf("0"); }
如果觉得有帮助,点个推荐啦~