基础实验4-2.3 二叉树的非递归遍历 (25分)

本题要求用非递归的方法实现对给定二叉树的 3 种遍历。

函数接口定义：

void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );

 

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
    int flag;
};

 

要求 3 个函数分别按照访问顺序打印出结点的内容，格式为一个空格跟着一个字符。

此外，裁判程序中给出了堆栈的全套操作，可以直接调用。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>
typedef enum { false, true } bool;

typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
    int flag;
};

/*------堆栈的定义-------*/
typedef Position SElementType;
typedef struct SNode *PtrToSNode;
struct SNode {
	SElementType Data;
	PtrToSNode Next;
};
typedef PtrToSNode Stack;

/* 裁判实现，细节不表 */
Stack CreateStack();
bool IsEmpty( Stack S );
bool Push( Stack S, SElementType X );
SElementType Pop( Stack S ); /* 删除并仅返回S的栈顶元素 */
SElementType Peek( Stack S );/* 仅返回S的栈顶元素 */
/*----堆栈的定义结束-----*/

BinTree CreateBinTree(); /* 裁判实现，细节不表 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );

int main()
{
    BinTree BT = CreateBinTree();
    printf("Inorder:");    InorderTraversal(BT);    printf("\n");
    printf("Preorder:");   PreorderTraversal(BT);   printf("\n");
    printf("Postorder:");  PostorderTraversal(BT);  printf("\n");
    return 0;
}
/* 你的代码将被嵌在这里 */

 

输入样例：

如图

 

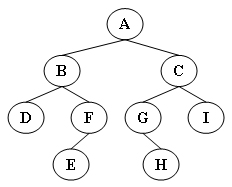
输出样例：

Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A

代码：

void InorderTraversal( BinTree BT ) {
    if(!BT) return;
    BinTree s[100] = {BT};
    int c = 1;
    while(c) {
        while(s[c - 1] -> Left) {
            s[c] = s[c - 1] -> Left;
            c ++;
        }
        while(c && s[c - 1] -> Right == NULL) printf(" %c",s[-- c] -> Data);
        if(c) {
            printf(" %c",s[c - 1] -> Data);
            s[c - 1] = s[c - 1] -> Right;
        }
    }
}
void PreorderTraversal( BinTree BT ) {
    if(!BT) return;
    BT -> flag = 0;
    BinTree s[100] = {BT};
    printf(" %c",BT -> Data);
    int c = 1;
    while(c) {
        while(s[c - 1] -> flag == 0 && s[c - 1] -> Left) {
            s[c - 1] -> flag = 1;
            s[c] = s[c - 1] -> Left;
            s[c] -> flag = 0;
            printf(" %c",s[c ++] -> Data);
        }
        while(c && s[c - 1] -> Right == NULL) c --;
        if(c) {
            s[c - 1] = s[c - 1] -> Right;
            s[c - 1] -> flag = 0;
            printf(" %c",s[c - 1] -> Data);
        }
    }
}
void PostorderTraversal( BinTree BT ) {
    if(!BT) return;
    BT -> flag = 0;
    BinTree s[100] = {BT};
    int c = 1;
    while(c) {
        BinTree temp = s[c - 1];
        if(temp -> flag == 0) {
            s[c - 1] -> flag = 1;
            if(temp -> Left) {
                s[c ++] = temp -> Left;
                s[c - 1] -> flag = 0;
            }
        }
        else if(temp -> flag == 1) {
            s[c - 1] -> flag = 2;
            if(temp -> Right) {
                s[c ++] = temp -> Right;
                s[c - 1] -> flag = 0;
            }
        }
        else {
            printf(" %c",s[-- c] -> Data);
        }
    }
}