最近点对问题

问题：设S是平面上n个点的集合，考虑在S种找到一个点对p和q，使其距离最短。求出其最短距离。

 

暴力检查每个点对并记录距离后可以选出最短距离，但时间复杂度是O(n²)。

这里可以运用一种分治的算法，使得时间复杂度降为O(nlogn)。

 

算法基本思路：

1.将所有点排序，优先考虑x，若x相等，则考虑y；

2.找到中间位置，将集合一分为二，在左边范围内求出最短距离L，在右边范围内求出最短距离R（集合一直划分至三个点后，直接暴力求解）；

3.现在考虑左边的点和右边的点组合能否产生更短的距离。因为现在知道L和R，求出两者中的较小值M，在中间位置各取左边M距离和右边M距离的空间，把其中的左边的点与右边的点暴力求距离值，然后将较小值与M比较，取更小的值即为结果（取2M距离是因为在这个距离外的点与对面的点的距离不可能小于M）。

 

　　　　　　　　　　　　

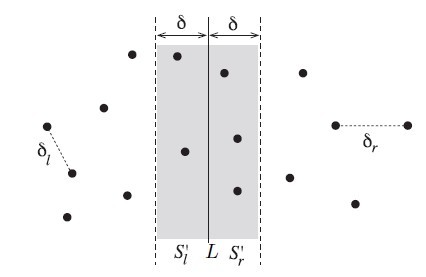
（图片参考自《ALGORITHMS DESIGN TECHNIQUES AND ANALYSIS》）

import java.util.Arrays;

class Point implements Comparable {
        
    double x;
    double y;

    public int compareTo(Object n){
        Point a = (Point)n;
        if(this.x != a.x){
            return (int)(this.x - a.x);
        }
        return (int)(this.y - a.y);
    }

    public String toString(){
        return "(" + x + ", " + y + ")";
    }
}

public class ClosestPair{

    public static double getClosestDistance(Point[] p){
        Arrays.sort(p);

        System.out.println(Arrays.toString(p));        //just for test
        
        return cp(p, 0, p.length-1);
    }

    private static double computeDistance(Point a, Point b){
        //compute the distance between two points
        return Math.sqrt(Math.pow((a.x-b.x), 2) + Math.pow((a.y-b.y), 2));
    }

    private static double cp(Point[] p, int low, int high){
        if(high - low + 1 <= 3){
            //less than 3, directly compute
            double min = computeDistance(p[low], p[high]);
            for(int i = low; i < high; i ++){
                for(int j = i+1; j <= high; j ++){
                    double temp = computeDistance(p[i], p[j]);
                    min = temp<min? temp:min;
                }
            }
            return min;
        }
        int mid = (low + high) / 2;
        double x0 = p[mid].x;
        //Divide
        double m = cp(p, low, mid);
        double n = cp(p, mid+1, high);
        //Conguer
        double min = m>n?n:m;
        int k = 0;
        //select the point that the distance between is and p[mid] may be less than min
        Point[] t = new Point[high-low+1];
        for(int i = low; i <= high; i ++){
            if(Math.abs(p[i].x - x0) <= min){
                t[k++] = p[i];
            }
        }
        double tmin = min * 2;
        for(int i = 0; i < k-1; i ++){
            for(int j = i+1; j < k; j ++){
                double temp = computeDistance(t[i], t[j]);
                tmin = temp<tmin? temp:tmin;
            }
        }
        min = tmin<min? tmin:min;
        return min;
    }

    public static void main(String[] args){
        Point[] p = new Point[5];
        for(int i = 0; i < p.length; i ++){
            p[i] = new Point();
            p[i].x = (int)(Math.random() * 100);
            p[i].y = (int)(Math.random() * 100);
        }
        System.out.println(getClosestDistance(p));
    }
}