【笔记】树/图上博弈

不一定是组合博弈。

ABC246G - Game on Tree 3

比较简单的树上博弈，首先答案具有单调性，我们直接二分答案然后 DP 判定即可。

P8276 [USACO22OPEN] Hoof and Brain P

图上博弈。

直接做没有什么思路，考虑从结束状态倒推。结束状态一定是一个棋子 \(b\) 堵住另一个棋子 \(a\)，并且 \(a\) 有唯一的出边 \(b\)。

所以如果一个点出度唯一，就可以将它和它的出点合并，为保证复杂度直接启发式合并即可。

P8173 「CEOI2021」 Newspapers

比较困难的树上博弈。

考虑手算一下长度为 \(5\) 的链。

不难发现最优策略就是 \(2,3,4,4,3,2\)，这给了我们很大的启发。

• 1.一定不能有环，否则任意情况对方都有两条路可走，永远无法抓住对方。

• 2.我们查询的过程类似于在树上移动，每次可以将路径上的点排除。一定是在相邻点上移动，否则如果对方在跳过的那个点上，你就永远不知道他的位置。

• 3.我们需要扫两遍，因为如果将树黑白染色，扫一遍只能排除一种颜色。

所以对于链的情况，一定有解且解为 \(2\to n -1,n-1\to 2\)，共 \(2n-2\) 次询问，可以得到 \(8\) 分。

扩展一下，如果链的某个节点上再接上一段会发生什么变化。

如果接上的是一个点，那么答案不会变化，因为该节点和连接的链上节点颜色相反，所以不是在第一遍被排除就是在第二遍被排除。

如果接上的链是两个点，那么我们只用多进行两次判断即可。

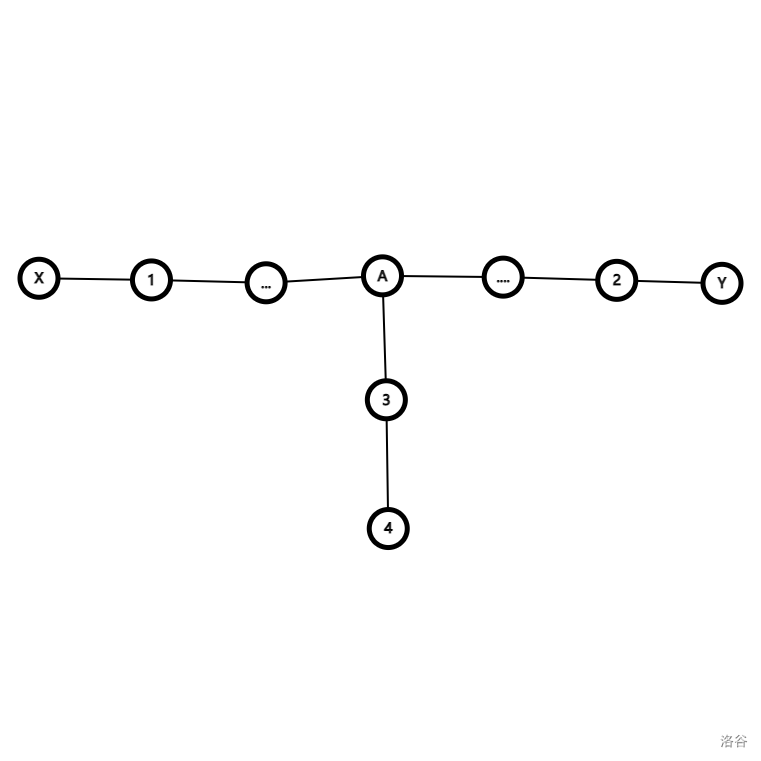
就是 \(1\to A\to3\to A\to 2\)，\(2\to A\to 3\to A\to 1\)。

如果接更多的节点呢，惊奇的发现我们不能更深入 \(4\) 号节点。

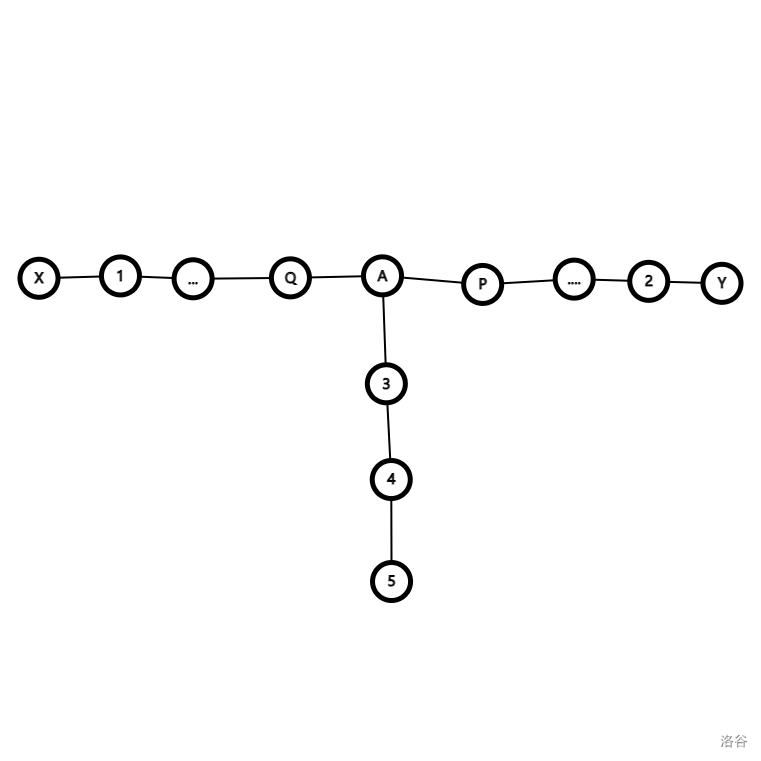
如果我们到达 \(4\) 号，再回到 \(A\)，那么进行 \(3\to 4\to 3\) 三次操作。这个时候如果对手在 \(P\) 或者 \(Q\) 号节点上，三次操作足够对方跨过 \(A\) 到达另一边。那么自己回到 \(A\) 的时候根本不知道对手在哪边，相当于前面的努力都白费了。

所以如果出现这种情况，两边都无法保全，只可能是无解。

这么分析后最优解应该很清晰了，我们找到直径，然后判断是否有长度 \(\ge 3\) 的支链，然后对于长度为 \(2\) 的支链要多进行两次操作进行覆盖。

时间复杂度 \(\mathcal{O}(N)\)，checker 的复杂度应该是 \(\mathcal{O}(N^2)\) 的。

P4654 [CEOI2017]Mousetrap

比较困难的树上博弈。

先令陷阱 \(t\) 为根，我们看老鼠会怎么决策。如果它往下走，最后会移动到叶子节点，那么它的运动就被锁死了，剩下的就完全在管理者的操控之内。那么我们就试着求出 \(f_{i}\) 表示老鼠进入以 \(i\) 为根的子树中，需要的操作数。那么老鼠一定会选择 \(f\) 最大的儿子，而我们一定会堵住这个儿子，所以老鼠一定会选择次大的儿子。

如果老鼠往上走，那么就需要考虑初始节点到根的路径上，侧接的子树的 \(f\)。直接求显然是不现实的，我们直接二分答案，如果子树 \(f\) 加上在初始节点到根路径上的操作数大于我们二分的 mid，那么这个子树必须被在老鼠到达之前堵住，我们让老鼠一直向上走，看是否有充足时间堵住这些子树。

---

树/图上博弈没有什么通解，是个和出题人斗智斗勇的过程。

比较好方法有观察比较小的样例/带入当事人视角/贪心决策/动态规划和二分思路/逆向思考结局倒推等。

思路必不能乱，毕竟出题人能想出来，说明题目的复杂性还是人力可及的。