【笔记】树状数组套主席树及其初步应用
0x00 前置芝士
必备芝士
- \(Binary\ \ Index\ \ Tree\)
- \(Persistent\ \ Segment\ \ Tree\)
什么?不会主席树,点击luogu题解然后成为大牛(讲解真的很好,Orz神犇
~当然,如果能提前了解下线段树套线段树和线段树套平衡树会更好(洛谷日报里貌似有一篇)
0x10 初探
0x11 总览
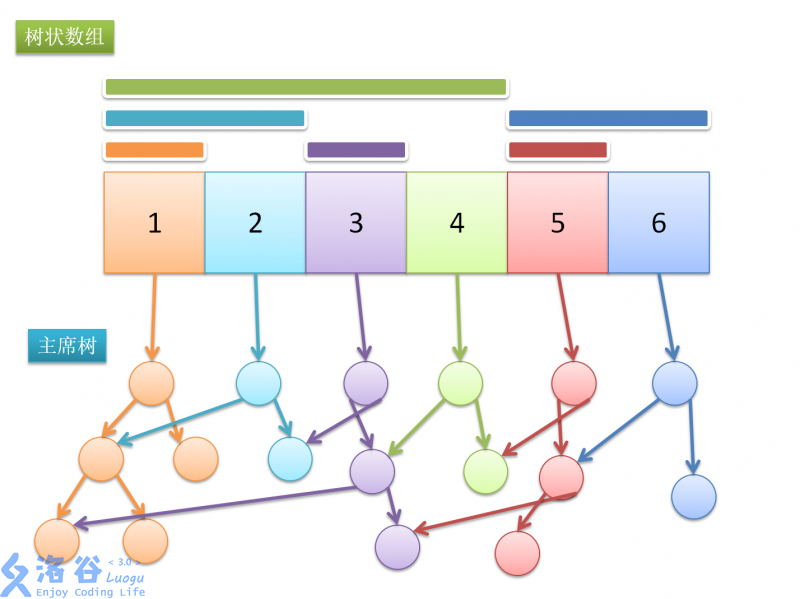
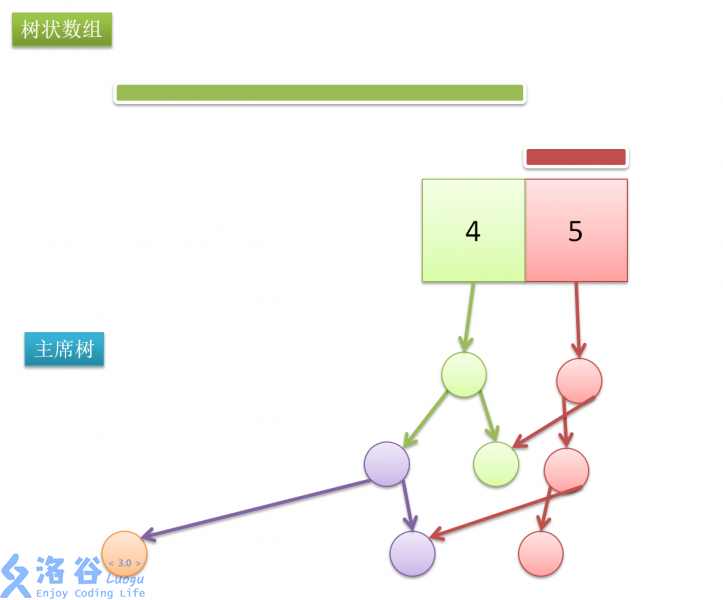
这幅图对后文理解有很大帮助(手画太丑轻喷
0x12 初步认识
树状数组可以在\(O(NlogN)\)的时间内维护区间前缀和和单点修改
主席树可以在在\(O(NlogN)\)的时空内维护一个线段树的所有历史状态
所以两者的结合可以在线维护各种带修改的序列操作
众所周知,树状数组它是个数组(不是树~
所以我们是数组套主席树(手动滑稽
因此我们可以建立一个树状数组,每个位置不再对应一个值,而是对应一棵主席树(划重点
树状数组第\(i\)个位置表示\(i-lowbit(i)+1\ \sim \ i\)的所有元素的和
现在我们树套树第\(i\)个位置表示\(i-lowbit(i)+1\ \sim \ i\)的所有元素构成的线段树
0x13 Q&A
为什么要用主席树(或动态开点线段树)?
- 因为直接开普通线段树,空间复杂度\(O(N^2)\),而主席树可以保证空间复杂度在空间限制以内
树状数组套主席树有什么用?
可以配main包夹绿鸟吃,可以碾压整体二分和\(CDQ\)分治在线解决序列上的复杂操作,强大功能将在后面详细介绍。更为重要的是,在时间复杂度和常数方面,树状数组套主席树远优于像线段树套平衡树/线段树,是在线解决序列问题的有力工具
为什么用树状数组而不用线段树?
- 首先树状数组的常数小于线段树的常数,并且主席树具有可加减性,所以我们使用树状数组就可以完成区间操作
0x14 关于序列上可持久化线段树和动态开点线段树的比较
目前网上的树状数组套主席树貌似是一个统称,主席树可以指序列上可持久化线段树或动态开点线段树。
简单地说,就是解决树状数组套主席树还是动态开点线段树的问题
- 如果不需要保存历史状态,动态开点线段树显然是优于主席树的
- 对于查询操作,两者的时间复杂度都是\(O(logN)\),常数相似(线段树的常数
- 对于修改操作,显然动态开点线段树的空间更优于主席树。因为主席树无论修改哪个位置,都会产生\(O(logN)\)个副本。对于动态开点线段树,如果修改一个以前已经修改的位置,则不需要再开点;总的来说,修改路径上的点如果已经开了点,则不需要再重新开点,所以平均每次新开的点远小于\(logN\)
- 两者空间相差\(2\sim 3\)倍
- 特别地说,如果想要在\(O(NlogN)\)的时间内统一初始化树套树而不是一个个往里加,则需要使用可持久化线段树
- 推荐树状数组套动态开点线段树(毕竟空间也是比较重要的资源),但具体用什么根据自己的习惯而定,如果空间要求比较严格的题目要特别注意一下
0x20 浅谈
0x21 建立主席树
先手写一棵主席树(难不成C++帮你写
struct node{
int l,r; //左右儿子
int data; //节点权值
}a[N*40];
int tot=0;
int build(int l,int r){ //构建一棵新树,如果是动态开点线段树则不需要
int p=++tot;
a[p].data=0;
if(l==r)return p;
int mid=(l+r)>>1;
a[p].l=build(l,mid);
a[p].r=build(mid+1,r);
return p;
}
int insert(int now,int l,int r,int to,int data){ //单点修改
int p=++tot;a[p]=a[now];
if(l==r){
a[p].data+=data;
return p;
}
int mid=(l+r)>>1;
if(mid>=to)a[p].l=insert(a[now].l,l,mid,to,data);
else a[p].r=insert(a[now].r,mid+1,r,to,data);
a[p].data=a[a[p].l].data+a[a[p].r].data;
return p;
}
//查询比较灵活,根据题面而定
(篇幅受限这里不再赘述主席树
0x22 初始化树套树
这一步真的是太简单了(手动滑稽
int root[N]; //初始空的树套树
void prevwork(){
int x=build(1,T);
for(int i=0;i<=n;i++)root[i]=x;
}
我们往往初始空树再把元素一个个往里加,因为一起加太复杂了
0x23 单点修改
直接上代码
int lb(int x){return x&-x;} //lowbit
//x表示树状数组中修改位置
//to表示线段树中修改位置
//data表示添加的值
void add(int x,int to,int data){
for(;x<=n;x+=lb(x))
root[x]=insert(root[x],1,T,to,data);
}
树状数组的单点修改是直接修改数组内一些元素
树套树的单点修改是修改树状数组中对应需要修改的位置对应主席树
例如\(N=6\)时修改位置\(1\):
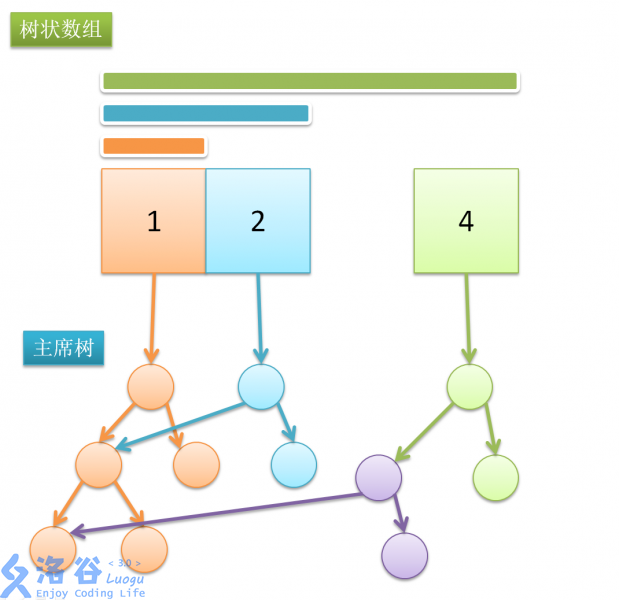
修改位置\(5\)
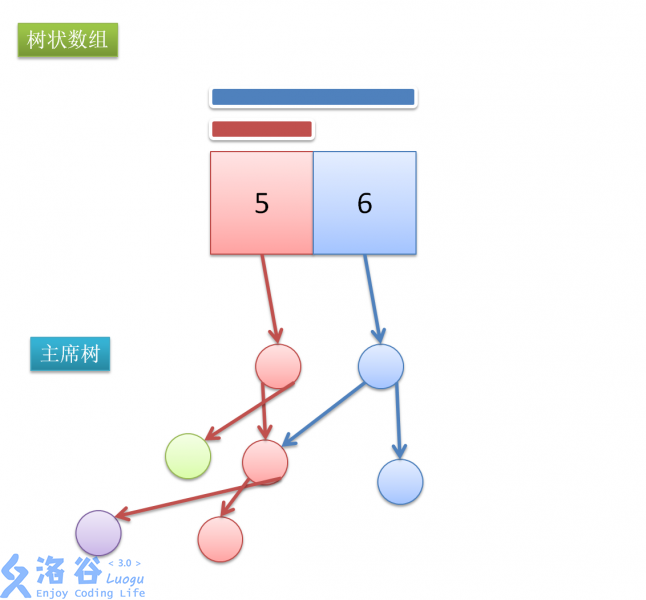
结合第一张图看
0x24 查询
主席树具有可加减的性质,即不同时间戮的主席树的内部构造是完全相同的,所以主席树的加减就是对应节点的加减
查询就是把树状数组中构成\(1\sim N\)前缀和的所有主席树加起来,再在得到的主席树中直接查询
例如查询\(Sum3\),则是将位置2的主席树和位置3的主席树相加:
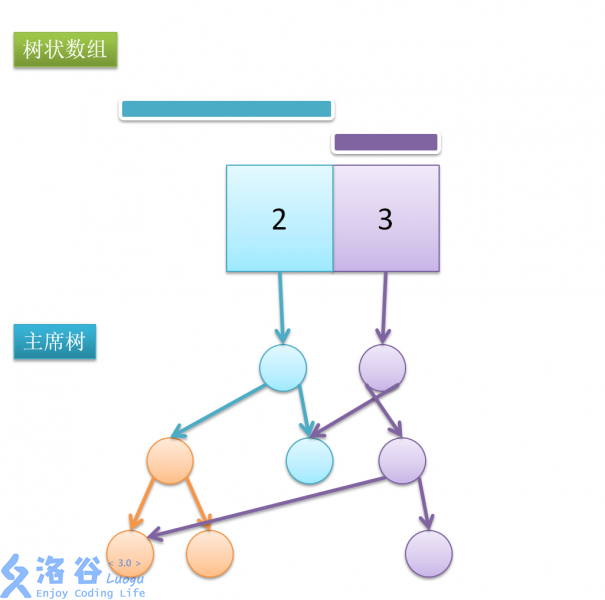
查询\(Sum5\)同理:
例题:求序列上\([x,y]\)中值域在\([L,R]\)中的数的和
就是求序列上\([1,y]\)中值域在\([L,R]\)中的数的和减去序列上\([1,x-1]\)中值域在\([L,R]\)中的数的和
直接在前缀和对应的位置的主席树上查询\([L,R]\)的数的个数,再一起求和得到最终答案
int ask(int x,int l,int r,int L,int R){ //主席树上查询
if(!x)return 0;
if(L<=l&&r<=R)return a[x].data;
int mid=(l+r)>>1;
int sum=0;
if(mid>=L)sum+=ask(a[x].l,l,mid,L,R);
if(mid<R)sum+=ask(a[x].r,mid+1,r,L,R);
return sum;
}
int aska(int x,int y,int L,int R){ //树状数组查询
if(L>R)return 0;
int sum=0;
for(;y;y-=lb(y)) //求Sum(y)
sum+=ask(root[y],1,n,L,R);
for(;x;x-=lb(x))
sum-=ask(root[x],1,n,L,R); //减去Sum(x-1)
return sum;
}
0x25 时间复杂度以及空间复杂度
对于查询操作,\(1\sim N\)的前缀和由\(O(logN)\)个位置的主席树构成(树状数组的基本性质),对于每棵主席树,查询需要\(O(logN)\)的时间(线段树的基本性质),所以单次查询的时间复杂度\(O(logN*logN)=O(log^2N)\)
对于单点修改操作,一共需要修改\(O(logN)\)个位置(树状数组的基本性质),主席树单点修改的时间复杂度和空间复杂度均为\(O(logN)\)(主席树的基本性质),
所以单次修改的时间和空间复杂度均为\(O(logN*logN)=O(log^2N)\)
显然如果\(N\)次操作,时间复杂度和空间复杂度均为\(O(N*logN*logN)=O(Nlog^2N)\)
0x30 树状数组套主席树实际应用
0x31 例题P2617 Dynamic Rankings(区间带修第\(K\)小)
众所周知,主席树可以在\(O(log N)\)的时间内求出第\(K\)小,且支持修改
所以树状数组套主席树可以支持单点修改区间第\(K\)小
-
0.读入所有操作,离散化
-
1.初始化树套树(0x21,0x22)
-
2.加入元素(0x23)
-
3.单点修改操作
就是删除该位置原来的数,加入修改后的数(0x23)
add(q[i].l,lower_bound(b+1,b+T+1,q[i].data)-b,1); add(q[i].l,lower_bound(b+1,b+T+1,u[q[i].l])-b,-1); -
4.查询操作(0x24)
int go1[200005],go2[200005]; void make(int i){ //得到构成前缀和1~i的主席树的所有的根节点 int topa=0,topb=0; for(int j=q[i].r;j;j-=lb(j))go1[++topa]=root[j]; for(int j=q[i].l-1;j;j-=lb(j))go2[++topb]=root[j]; } int ask(int l,int r,int k,int topa,int topb){ if(l==r)return l; //查询,类似于主席树模板,只不过现在是多棵主席树相加减 int mid=(l+r)>>1; int sum=0; for(int i=1;i<=topa;i++)sum+=a[a[go1[i]].l].data; for(int i=1;i<=topb;i++)sum-=a[a[go2[i]].l].data; if(sum>=k){ for(int i=1;i<=topa;i++)go1[i]=a[go1[i]].l; for(int i=1;i<=topb;i++)go2[i]=a[go2[i]].l; return ask(l,mid,k,topa,topb); } for(int i=1;i<=topa;i++)go1[i]=a[go1[i]].r; for(int i=1;i<=topb;i++)go2[i]=a[go2[i]].r; return ask(mid+1,r,k-sum,topa,topb); }
完整程序\(Code\ O(Nlog^2N)\):
#include<bits/stdc++.h>
using namespace std;
struct node{
int l,r;
int data;
}a[60000005];
struct Q{
int l,r,data,opt;
}q[100005];
int n,m,t,T,tot;
int u[200005],v[200005],b[200005],root[200005];
int build(int l,int r){
int p=++tot;
a[p].data=0;
if(l==r)return p;
int mid=(l+r)>>1;
a[p].l=build(l,mid);
a[p].r=build(mid+1,r);
return p;
}
int insert(int now,int l,int r,int to,int data){
int p=++tot;a[p]=a[now];
if(l==r){
a[p].data+=data;
return p;
}
int mid=(l+r)>>1;
if(mid>=to)a[p].l=insert(a[now].l,l,mid,to,data);
else a[p].r=insert(a[now].r,mid+1,r,to,data);
a[p].data=a[a[p].l].data+a[a[p].r].data;
return p;
}
int lb(int x){return x&-x;}
void add(int x,int to,int data){
for(;x<=n;x+=lb(x))
root[x]=insert(root[x],1,T,to,data);
}
int go1[200005],go2[200005];
int ask(int l,int r,int k,int topa,int topb){
if(l==r)return l;
int mid=(l+r)>>1;
int sum=0;
for(int i=1;i<=topa;i++)sum+=a[a[go1[i]].l].data;
for(int i=1;i<=topb;i++)sum-=a[a[go2[i]].l].data;
if(sum>=k){
for(int i=1;i<=topa;i++)go1[i]=a[go1[i]].l;
for(int i=1;i<=topb;i++)go2[i]=a[go2[i]].l;
return ask(l,mid,k,topa,topb);
}
for(int i=1;i<=topa;i++)go1[i]=a[go1[i]].r;
for(int i=1;i<=topb;i++)go2[i]=a[go2[i]].r;
return ask(mid+1,r,k-sum,topa,topb);
}
void prev_work(){
sort(v+1,v+t+1);
v[0]=(1<<30);
for(int i=1;i<=t;i++){
if(v[i]!=v[i-1])
b[++T]=v[i];
}
int x=build(1,T);
for(int i=0;i<=n;i++)root[i]=x;
for(int i=1;i<=n;i++)
add(i,lower_bound(b+1,b+T+1,u[i])-b,1);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&u[i]),v[++t]=u[i];
for(int i=1;i<=m;i++){
char opt[2];
scanf("%s",opt);
if(opt[0]=='C'){
q[i].opt=0;
scanf("%d%d",&q[i].l,&q[i].data);
v[++t]=q[i].data;
}
else{
scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].data);
q[i].opt=1;
}
}
prev_work();
for(int i=1;i<=m;i++){
if(q[i].opt){
int topa=0,topb=0;
for(int j=q[i].r;j;j-=lb(j))go1[++topa]=root[j];
for(int j=q[i].l-1;j;j-=lb(j))go2[++topb]=root[j];
printf("%d\n",b[ask(1,T,q[i].data,topa,topb)]);
}
else{
add(q[i].l,lower_bound(b+1,b+T+1,q[i].data)-b,1);
add(q[i].l,lower_bound(b+1,b+T+1,u[q[i].l])-b,-1);
u[q[i].l]=q[i].data;
}
}
return 0;
}
\(Hint:\)例题的扩展,单点修改,区间第\(K\)大,区间排名,区间前驱和后继(事实上都是权值线段树的基本操作),因为带单点修改,所以直接在外面套一层树状数组即可,权值线段树要可持久化
0x32例题P4175 [CTSC2008]网络管理(树上点修路径上第\(K\)大)
题面扯这么长实际上题意就是上面那句话
对于不带修改的路径第\(K\)小,直接跑P2633 Count on a tree,每个节点保存它到根的路径上的所有点权构成的主席树,查询时利用主席树的加减得到路径上点权构成的主席树,然后直接跑主席树模板
现在我们考虑树上的单点修改。显然,修改树上的一个节点,以它为根的整棵子树的每个节点的信息都要修改,就是分别在子树中每个节点的主席树中删除该点原来的点权,插入现在的点权
由于是对整棵子树的整体修改(很熟悉吧),我们可以借助\(DFS\)序,将子树操作转化为序列操作,将树上点修路径上第\(K\)大转化为区间修改单点查询第\(K\)大,借助树状数组的基本差分操作转化为单点修改前缀和查询第\(K\)大,就是0x31例题P2617 Dynamic Rankings,第\(K\)小变成第\(K\)大
点到为止,细节仔细思考一下(其实是我懒,求饶
完整程序\(Code\ O(Nlog^2N)\):
// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define N 160005
using namespace std;
int n,m;
struct node{
int l,r;
int sum;
}a[N<<7];
int tot=0;
int build(int l,int r){
int p=++tot;
a[p].sum=0;
if(l==r)return p;
int mid=(l+r)>>1;
a[p].l=build(l,mid);
a[p].r=build(mid+1,r);
return p;
}
int insert(int now,int l,int r,int to,int val){
int p=++tot;
a[p]=a[now];
if(l==r){
a[p].sum+=val;
return p;
}
int mid=(l+r)>>1;
if(mid>=to)a[p].l=insert(a[now].l,l,mid,to,val);
else a[p].r=insert(a[now].r,mid+1,r,to,val);
a[p].sum=a[a[p].l].sum+a[a[p].r].sum;
return p;
}
int v[N],u[N],b[N],top;
struct Q{int k,a,b;}q[N];
struct edge{
int to;
int next;
}e[N<<1];
int h[N],pop=0,w;
void add(int x,int y){
e[++pop].to=y;
e[pop].next=h[x];
h[x]=pop;
}
int L[N],root[N],cnt=0,fa[N][26],size[N],d[N];
void dfs(int x,int f){
L[x]=++cnt;fa[x][0]=f;
root[x]=insert(root[f],1,top,lower_bound(b,b+top+1,v[x])-b,1);
size[x]=1;d[x]=d[f]+1;
for(int i=1;i<=24;i++)fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=h[x];i;i=e[i].next)
if(e[i].to!=f)
dfs(e[i].to,x),size[x]+=size[e[i].to];
}
int lca(int x,int y){
if(d[x]>d[y])swap(x,y);
for(int i=24;i>=0;i--)
if(d[fa[y][i]]>=d[x])y=fa[y][i];
if(y==x)return x;
for(int i=24;i>=0;i--)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
int c[N];
int lowbit(int x){return x&-x;}
void change(int x,int to,int val){
for(;x<=n;x+=lowbit(x))
c[x]=insert(c[x],1,top,to,val);
}
int arr[100],p[5][100],len[5],ne[5];
int get(int x){
int tt=0;
for(;x;x-=lowbit(x))
arr[++tt]=c[x];
return tt;
}
int ask(int P,int Q,int R,int C,int l,int r,int k){
if(l==r)return l;
int sum=(a[a[P].r].sum+a[a[Q].r].sum-a[a[R].r].sum-a[a[C].r].sum);
for(int i=1;i<=len[1];i++)
sum+=a[a[p[1][i]].r].sum;
for(int i=1;i<=len[2];i++)
sum+=a[a[p[2][i]].r].sum;
for(int i=1;i<=len[3];i++)
sum-=a[a[p[3][i]].r].sum;
for(int i=1;i<=len[4];i++)
sum-=a[a[p[4][i]].r].sum;
int mid=(l+r)>>1;
if(sum>=k){
for(int j=1;j<=4;j++)
for(int i=1;i<=len[j];i++)
p[j][i]=a[p[j][i]].r;
return ask(a[P].r,a[Q].r,a[R].r,a[C].r,mid+1,r,k);
}
else{
for(int j=1;j<=4;j++)
for(int i=1;i<=len[j];i++)
p[j][i]=a[p[j][i]].l;
return ask(a[P].l,a[Q].l,a[R].l,a[C].l,l,mid,k-sum);
}
}
int main()
{
scanf("%d%d",&n,&m);w=n;
for(int i=1;i<=n;i++)scanf("%d",&v[i]),u[i]=v[i];
for(int i=1;i<n;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);add(y,x);
}
for(int i=1;i<=m;i++){
scanf("%d%d%d",&q[i].k,&q[i].a,&q[i].b);
if(!q[i].k)u[++w]=q[i].b;
}
sort(u+1,u+w+1);
for(int i=1;i<=w;i++)
if(u[i]!=u[i-1])
b[++top]=u[i];
root[0]=build(1,top);
dfs(1,0);
for(int i=1;i<=n;i++)
c[i]=root[0];
for(int i=1;i<=m;i++){
if(!q[i].k){
change(L[q[i].a],lower_bound(b+1,b+top+1,v[q[i].a])-b,-1);
change(L[q[i].a]+size[q[i].a],lower_bound(b+1,b+top+1,v[q[i].a])-b,1);
change(L[q[i].a],lower_bound(b+1,b+top+1,q[i].b)-b,1);
change(L[q[i].a]+size[q[i].a],lower_bound(b+1,b+top+1,q[i].b)-b,-1);
v[q[i].a]=q[i].b;
}
else{
ne[1]=q[i].a;ne[2]=q[i].b;ne[3]=lca(q[i].a,q[i].b);ne[4]=fa[ne[3]][0];
///for(int j=1;j<=4;j++)
//printf("%d ",ne[j]);puts("");
for(int j=1;j<=4;j++)
{
len[j]=get(L[ne[j]]);
for(int k=1;k<=len[j];k++)
p[j][k]=arr[k];
//cout<<p[j][k];
}
int sum=a[root[ne[1]]].sum+a[root[ne[2]]].sum-a[root[ne[3]]].sum-a[root[ne[4]]].sum;
for(int j=1;j<=len[1];j++)
sum+=a[p[1][j]].sum;
for(int j=1;j<=len[2];j++)
sum+=a[p[2][j]].sum;
for(int j=1;j<=len[3];j++)
sum-=a[p[3][j]].sum;
for(int j=1;j<=len[4];j++)
sum-=a[p[4][j]].sum;
if(sum<q[i].k)printf("invalid request!\n");
else printf("%d\n",b[ask(root[ne[1]],root[ne[2]],root[ne[3]],root[ne[4]],1,top,q[i].k)]);
}
}
return 0;
}
0x33 P3157 [CQOI2011]动态逆序对
(还记得**0x20**麽_
求逆序对有归并排序和树状数组两种方法,是否了解这两种方法分别是什么原理
归并排序运用分治思想,统计\([l,r]\)的逆序对,分别考虑左右端点都在\([l,mid]\)的逆序对、左右端点都在\([mid+1,r]\)的逆序对和左右端点分别在\([l,mid]\)和\([mid+1]\)的逆序对。前二者递归下去求解,后者在归并的时候进行统计
树状数组求解则运用了离线分类思想,通俗的说,就是固定右端点,有多少个左端点和它构成逆序对
现在我们做动态逆序对无疑也是这样,首先初始化,并将原始序列排序得到最初的逆序对数
对于删除操作,对答案的贡献无疑有两种,一是这个数作为逆序对的右端点,二是这个数作为逆序对的左端点,这两种逆序对在删除后都不复存在了
\(x\)表示删除的位置,\(u[x]\)表示这个位置的权值
对于第一种,我们查询\([1,x-1]\)中有多少个数位于值域\([u[x]+1,n]\),即位置在它之前并且权值比它大,在答案中减去
对于第二种,同理我们查询\([x+1,n]\)中有多少个数位于值域\([1,u[x]-1]\),在答案中减去
最后删除这个位置的权值,即
add(x,u[x],-1);
具体操作分别见0x22,0x23,0x24;
另外,这题恶意卡主席树空间,\(128M\)会爆炸,解决方案是使用动态开点线段树替换可持久化线段树,思路完全一样(我也是现在才学到动态开点线段树这玩意,细节见程序)
为什么动态开点线段树要省空间?
- 因为主席树无论插入还是删除都要新开空间,而动态开点线段树只有在加入新数时才会开空间(当然,动态开点线段树不能代替主席树,因为它不能保存所有的历史状态)
\(Code\ O(Nlog^2N):\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node{
int l,r;
int data;
}a[12000003];
int n,m,t,T,tot=0;
int u[100005],v[100005],b[100005],root[100005];
int insert(int x,int l,int r,int to,int data){
if(!x)x=++tot;
if(l==r){
a[x].data+=data;
return x;
}
int mid=(l+r)>>1;
if(mid>=to)a[x].l=insert(a[x].l,l,mid,to,data);
else a[x].r=insert(a[x].r,mid+1,r,to,data);
a[x].data=a[a[x].l].data+a[a[x].r].data;
return x;
}
int lb(int x){return x&-x;}
void add(int x,int to,int data){
for(;x<=n;x+=lb(x))
insert(root[x],1,n,to,data);
}
int ask(int x,int l,int r,int L,int R){
if(!x)return 0;
if(L<=l&&r<=R)return a[x].data;
int mid=(l+r)>>1;
int sum=0;
if(mid>=L)sum+=ask(a[x].l,l,mid,L,R);
if(mid<R)sum+=ask(a[x].r,mid+1,r,L,R);
return sum;
}
int aska(int x,int L,int R){
if(L>R)return 0;
int sum=0;
for(;x;x-=lb(x))
sum+=ask(root[x],1,n,L,R);
return sum;
}
int o[100005],to[100005];
ll ans=0;
void msort(int l,int r){
if(l==r)return;
int mid=(l+r)>>1;
msort(l,mid);msort(mid+1,r);
int L=l,R=mid+1,top=0;
for(int i=l;i<=r;i++){
if(R>r||(o[L]<=o[R]&&L<=mid))
b[++top]=o[L++];
else {
if(o[L]>o[R])ans+=(ll)mid-L+1;
b[++top]=o[R++];
}
}
for(int i=1;i<=top;i++)
o[l+i-1]=b[i];
}
int f[100005];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&o[i]),to[o[i]]=i,f[i]=o[i];
msort(1,n);
for(int i=1;i<=n;i++)
root[i]=++tot;
for(int i=1;i<=n;i++)
add(i,f[i],1);
for(int i=1;i<=m;i++){
printf("%lld\n",ans);
int x;scanf("%d",&x);x=to[x];
//cout<<x<<" "<<f[x]<<" tt"<<endl;
//printf("%d %d %d\n",aska(x-1,f[x],n),aska(n,1,f[x]-1),aska(x-1,1,f[x]-1));
ans-=(ll)aska(x-1,f[x],n)+aska(n,1,f[x]-1)-aska(x-1,1,f[x]-1);
add(x,f[x],-1);
}
return 0;
}
习题P3759 [TJOI2017]不勤劳的图书管理员~(吐槽:题面描述不清,暴力都能过……
习题P1975 [国家集训队]排队(话说线段树套平衡树都可以过,但貌似暴力过不去了
习题CF785E Anton and Permutation(CF的题才像个样子嘛
将会陆续咕咕咕地更新(假
感谢阅读,下方评论


 浙公网安备 33010602011771号
浙公网安备 33010602011771号