【题解】[JOISC2020] 治療計画

最关键的一步，转化为最短路。

对于每个方案我们看成一个点，对于两个方案 \(i,j\) ，当且仅当 \(R_i-L_j+1\ge|T_i-T_j|\) 时，从点 \(i\) 向点 \(j\) 连边。

形象化的，我们将时间作为纵轴，房屋作为横轴，发现一次治疗就是一条平行于横轴的路径，而两次治疗之间的衔接恰好是一条斜率为 \(1\) 或 \(-1\) 的直线。所以最短路就是答案。

放一张图便于理解。

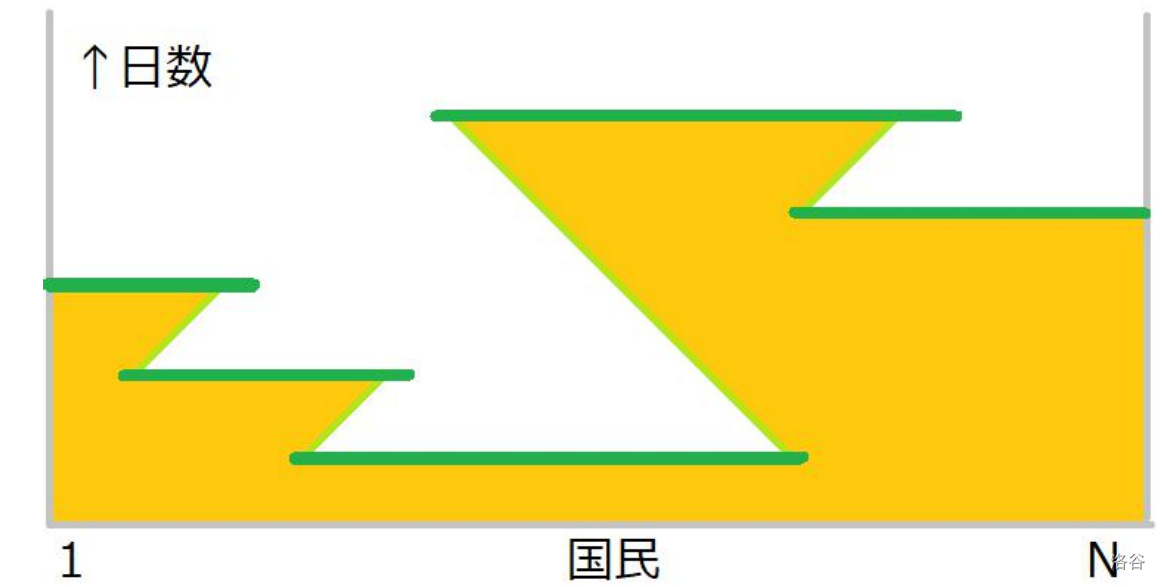
直接建图跑最短路是 \(\mathcal{O}(N^2)\) 的，考虑优化建图。

我们对所有点按 \(T_i\) 排序，那么当 \(T_i\ge T_j\) 时，有 \(R_i-T_i+1\ge L_j-T_j\) ，否则是 \(R_i+T_i+1\ge L_j+T_j\) 。

式子一边只与 \(i,j\) 中的一个有关，可以看作点的属性，那么我们只需要再满足 \(T_i\) 和 \(T_j\) 的大小关系。

直接线段树优化建图。线段树优化的最短路有一个优美的性质就是线段树上的边只会转移一次，所以时间复杂度是 \(\mathcal{O}(N\log N)\) 。

关于这个性质可以参考这道经典题，也是线段树优化最短路。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 100005
const int inf = 0x7fffffff;
using namespace std;
int n,m,v[N];long long d[N];
struct node{
	int t,l,r,c;
	bool operator<(const node o)const{return t<o.t;}
}u[N];
struct Node{
	int l,r,mna,mnb;
}a[N<<2];
#define L a[x].l
#define R a[x].r
#define ls (x<<1)
#define rs (ls|1)
#define A a[x].mna
#define B a[x].mnb
void updata(int x){
	A=min(a[ls].mna,a[rs].mna);
	B=min(a[ls].mnb,a[rs].mnb);
}
void build(int x,int l,int r){
	L=l,R=r;
	if(l==r){
		A=u[l].l-u[l].t;
		B=u[l].l+u[l].t;
		//cout<<"build  "<<l<<" "<<A<<" "<<B<<endl;
	}
	else{
		int mid=(l+r)>>1;
		build(ls,l,mid);
		build(rs,mid+1,r);
		updata(x);
	}
}
priority_queue<pair<long long,int> >q;
void solve(int x,int l,int r,int val,long long ds){
	//cout<<"AA "<<x<<" "<<l<<" "<<r<<" "<<val<<" "<<ds<<" "<<L<<" "<<R<<" "<<A<<endl;
	if(A>val)return;
	if(L==R){
		if(ds+u[L].c<d[L])d[L]=ds+u[L].c,q.push(make_pair(-d[L],L));
		A=B=inf;return;
	}
	if(L>=l&&R<=r){
		solve(ls,l,r,val,ds);
		solve(rs,l,r,val,ds);
		updata(x);return;
	}
	int mid=(L+R)>>1;
	if(mid>=l)solve(ls,l,r,val,ds);
	if(mid<r)solve(rs,l,r,val,ds);
	updata(x);
}
void calc(int x,int l,int r,int val,long long ds){
	//cout<<"BB "<<x<<" "<<l<<" "<<r<<" "<<val<<" "<<ds<<" "<<L<<" "<<R<<" "<<B<<endl;
	if(B>val)return;
	if(L==R){
		//cout<<"OK "<<l<<" "<<ds<<" "<<u[l].c<<" "<<d[l]<<endl;
		if(ds+u[L].c<d[L])d[L]=ds+u[L].c,q.push(make_pair(-d[L],L));
		A=B=inf;return;
	}
	if(L>=l&&R<=r){
		calc(ls,l,r,val,ds);
		calc(rs,l,r,val,ds);
		updata(x);return;
	}
	int mid=(L+R)>>1;
	if(mid>=l)calc(ls,l,r,val,ds);
	if(mid<r)calc(rs,l,r,val,ds);
	updata(x);
}
void dij(){
	rep(i,1,m)if(u[i].l==1)d[i]=u[i].c,q.push(make_pair(-d[i],i));else d[i]=0x7fffffffffffffffLL;
	//cout<<a[1].mna<<" "<<a[1].mnb<<endl;
	while(!q.empty()){
		int x=q.top().second;q.pop();v[x]=1;
		//cout<<"ss "<<x<<" "<<d[x]<<" "<<u[x].r-u[x].t+1<<" "<<u[x].r+u[x].t+1<<endl;
		if(u[x].r==n){printf("%lld\n",d[x]);return;}
		solve(1,1,x,u[x].r-u[x].t+1,d[x]);calc(1,x,m,u[x].r+u[x].t+1,d[x]);
		while(!q.empty()&&v[q.top().second])q.pop();
	}
	puts("-1");
}
int main(){
	scanf("%d%d",&n,&m);
	rep(i,1,m)scanf("%d%d%d%d",&u[i].t,&u[i].l,&u[i].r,&u[i].c);
	sort(u+1,u+m+1);
	//rep(i,1,m)printf("cc  %d %d %d %d\n",u[i].t,u[i].l,u[i].r,u[i].c);
	build(1,1,m);dij();
	return 0;
}